Berekeningsgids voor het ontwerpen van een geïsoleerde fundering op basis van CSA A23.3-14

SkyCiv Foundation dekt het ontwerp van geïsoleerde fundering conform CSA A23.3-14¹ en NBCC 2010².

Wil je de Foundation Design-software van SkyCiv proberen?? Met onze tool kunnen gebruikers Foundation Design-berekeningen uitvoeren zonder enige download of installatie!

Stichting ontwerp rekenmachine

Ontwerpparameters van een geïsoleerde fundering

Sommige gepresenteerde berekeningen zijn vergelijkbaar met ACI 318, dat ook een van de referenties is van zijn CSA-tegenhanger.

Dimensievereisten:

Om de afmetingen van een geïsoleerde voet te bepalen, service of niet-gefactureerde belastingen, zoals dood (D), Leven (L), Wind (W), Seismisch (E), etc zal worden toegepast met behulp van Load Combinations, zoals gedefinieerd door NBCC 2010. Welke belastingcombinatie ook van toepassing is, wordt beschouwd als de ontwerpbelasting, en wordt verdeeld naar de toegestane bodemdruk, zoals weergegeven in de vergelijking 1.

\(\tekst{A} = frac{\tekst{P.}_{\tekst{n}}}{\tekst{q}_{\tekst{alle}}} \rechter pijl \) Vergelijking 1

waar:
q_alle = toelaatbare bodemdruk
P._n = niet-gefactureerde ontwerpbelasting
A = Funderingsgebied

Eenrichtingsschaar

Om te controleren eenrichtingsschaar, het kritische schuifvlak (Zie afbeelding 1) bevindt zich op afstand “d” van het gezicht van een kolom.

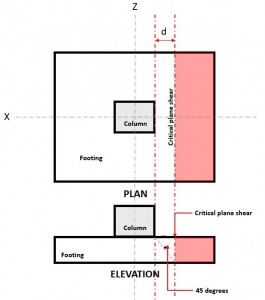
Figuur 1. Kritische vlakscheerbeurt van eenrichtingsschaar

De Een manier Schuintrekken Vraag naar of V _f wordt berekend in de veronderstelling dat de voet vrijdragend is weg van de kolom waar het gebied is (rood) aangegeven in figuur 2, in overeenstemming met CSA A23.3-14, Sectie 13.3.6.

De Afschuifcapaciteit in één richting of V _c wordt gedefinieerd als ultieme afschuifsterkte en berekend met behulp van vergelijking 2 per CSA A23.3-14, Sectie 11.3.4.

\(\tekst{V }_{\tekst{c}} = phi _{\tekst{c}} \tijden lambda times sqrt{\tekst{F'}_{\tekst{c}}} \keer tekst{b}_{\tekst{w}} \keer tekst{d} \rechter pijl \) Vergelijking 2 (CSA A23.3-14 Vgl. 11-6)

waar:
φ_c = weerstandsfactor voor beton
λ = modificatiefactor voor betondichtheid
f’_c = gespecificeerde betonsterkte, MPa
b_w = breedte van de voet, mm
d = effectieve afschuifdiepte, mm

Afschuifvraag en afschuifcapaciteit moeten aan de volgende vergelijking voldoen om aan de ontwerpvereisten te voldoen CSA A23.3-14:

\(\tekst{V }_{\tekst{f}} \lees phitext{V }_{\tekst{c}} \rechter pijl \) Vergelijking 3 (CSA A23.3-14 Eq. 11.3)

SkyCiv Foundation, in overeenstemming met vergelijking 3, berekent de one-way shear unity ratio (Vergelijking 4) door de afschuifvraag te nemen boven de afschuifcapaciteit.

\( \tekst{eenheidsratio} = frac{\tekst{Vraag naar schuifkracht}}{\tekst{Afschuifcapaciteit:}} \rechter pijl \) Vergelijking 4

Tweerichtingsschaar

De Tweerichtingsschaar grenstoestand:, ook gekend als ponsschaar, breidt het kritische gedeelte uit tot een afstand “d/2” vanaf de voorkant van de kolom en rond de omtrek van de kolom. Het kritieke afschuifvlak bevindt zich op dat deel van de fundering (Zie afbeelding 2).

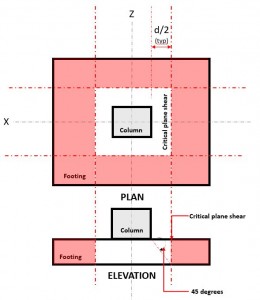
Figuur 2. Kritisch afschuifvlak van bidirectionele afschuiving:

De Twee manierenhoor vraag of V _f vindt plaats in het kritische afschuifvlak, gelegen op een afstand van “d/2” waar de (rood) gearceerd gebied, aangegeven in figuur 2, in overeenstemming met CSA A23.3-14, Sectie 13.3.3.

De Afschuifcapaciteit: of V _c wordt bepaald door de kleinste waarde die is berekend met behulp van vergelijking 5, 6, en 7 per CSA A23.3-14, Sectie 13.3.4.1

\(\tekst{V }_{\tekst{c}} = links ( 1 + \frac{2}{\zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt{\tekst{c}}} \Rechtsaf ) \keer 0.19 \tijden lambda tijden phi _{\tekst{c}} \keer sqrt{f'_{c}} \rechter pijl \) Vergelijking 5 (CSA A23.3-14 Eq. 13.5)

\(\tekst{V }_{\tekst{c}} = links ( \frac{\alfa_{\tekst{s}} \keer tekst{d}}{\tekst{b}_{\tekst{De}}} + 0.19 \Rechtsaf ) \tijden lambda tijden phi _{\tekst{c}} \keer sqrt{f'_{c}} \rechter pijl \) Vergelijking 6 (CSA A23.3-14 Eq. 13.6)

\(\tekst{V }_{\tekst{c}} = 0.38 \tijden lambda tijden phi _{\tekst{c}} \keer sqrt{f'_{c}} \rechter pijl \) Vergelijking 7 (CSA A23.3-14 Eq. 13.7)

Notitie: b_c is de verhouding tussen de lange zijde en de korte zijde van de kolom, geconcentreerde lading, of reactiegebied en α_s is gegeven door 13.3.4.1

waar:
λ = modificatiefactor voor betondichtheid
f’_c = gespecificeerde drukbetonsterkte, MPa
d = afstand van extreme compressievezel tot zwaartepunt van longitudinale trekwapening, mm

Afschuifvraag en afschuifcapaciteit moeten aan de volgende vergelijking voldoen om te voldoen aan de ontwerpvereisten van CSA A23.3-14:

\(\tekst{V }_{\tekst{f}} \lees phitext{V }_{\tekst{c}} \rechter pijl \) Vergelijking 8 (CSA A23.3-14 Eq. 11.3)

SkyCiv Foundation, in overeenstemming met vergelijking 8, berekent de tweerichtingsschuifeenheidverhouding (Vergelijking 9) door de afschuifvraag te nemen boven de afschuifcapaciteit.

\( \tekst{eenheidsratio} = frac{\tekst{Vraag naar schuifkracht}}{\tekst{Afschuifcapaciteit:}} \rechter pijl \) Vergelijking 9

Buiging

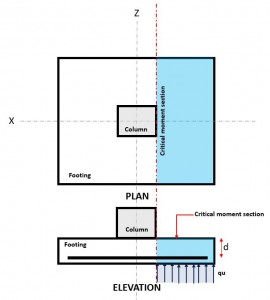
Figuur 3. Kritische buigingssectie

De buigzaam grenstoestand treedt op de sectie kritische buiging, gelegen aan de voorkant van de kolom bovenop de voet (Zie afbeelding 3).

De Momentvraag, of M_f bevindt zich op de afdeling kritische buiging (blauw luikgebied) aangegeven in figuur 3, en wordt berekend met behulp van vergelijking 10.

\( \tekst{M}_{u} = tekst{q}_{u} \keer links ( \frac{l_{X}}{2} – \frac{c_{X}}{2} \Rechtsaf ) \keer l_{z} \keer links ( \frac{\frac{l_{X}}{2} – \frac{c_{X}}{2} }{2} \Rechtsaf ) \rechter pijl \) Vergelijking 10

waar:
q_u = meegerekende bodemdruk, kPa
l_X = voetafmeting langs de x-as, mm
l_z = voetmaat langs de z-as, mm
c_X = kolomdimensie langs de x-as, mm

De Moment weerstand, of Mr wordt berekend met behulp van vergelijking 11.

\( \tekst{M}_{r} = phi_{\tekst{s}} \keren per_{s} \keer f_{j} \keer links( d – \frac{een}{2} \Rechtsaf) \rechter pijl \) Vergelijking 11

waar:
φ_s = weerstandsfactor voor niet-voorgespannen wapeningsstaven
d = afstand van extreme compressievezel tot zwaartepunt van longitudinale trekwapening, mm
A_s = versterkingsgebied, mm²
a = diepte van equivalent rechthoekig spanningsblok, mm
fy = versterkingssterkte, MPa

NIEUWE SkyCiv Foundation met FEA

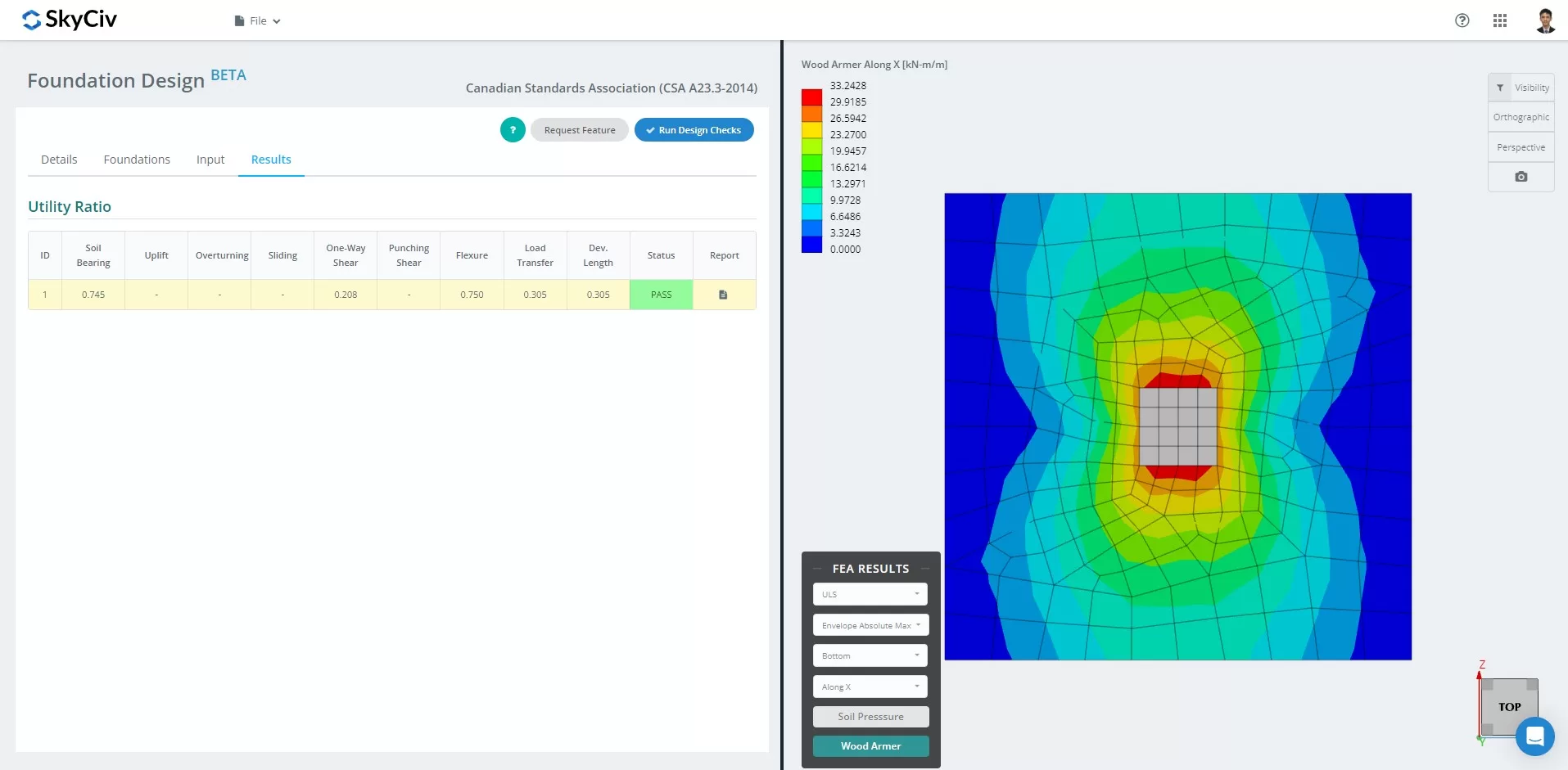
Vanaf maart 2024, de Foundation Design Module heeft de Eindige Elementenanalyse geïntegreerd (LELIJK) oplosser in zijn mogelijkheden. This new feature allows users to conduct in-depth soil pressure and wood armer analyses while still performing all structural checks specified by CSA A23.3-14, inclusief alle bovengenoemde verificaties. Een samenvatting van de FEA-resultaten is opgenomen in het uitgebreide rapport.