Straalgedrag: Momentcapaciteit van een balk

Voordat we de berekening van de momentcapaciteit bespreken, laten we het gedrag van a . bekijken gewapend beton eenvoudige balk als de belasting op de balk toeneemt van nul tot de grootte die storing zou veroorzaken. De balk zal worden onderworpen aan neerwaartse belasting, wat een positief moment in de straal zal veroorzaken. De stalen versteviging bevindt zich nabij de onderkant van de balk, dat is de spankant. Hier kunnen we drie belangrijke gedragsmodi van de bundel selecteren:

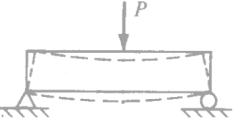
1. Buiggedrag bij een zeer kleine belasting

Ervan uitgaande dat de beton Ervan uitgaande dat de. Ook beton aan de bovenkant is bestand tegen compressie. De spanningsverdeling is lineair:

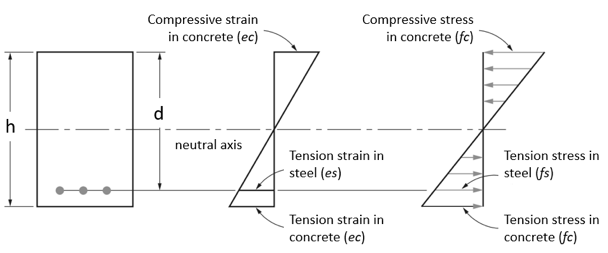
2. Buiggedrag bij matige belasting

In dit geval, de treksterkte van het beton wordt overschreden, en het beton zal barsten in de trekzone. Omdat het beton geen spanning over een scheur kan overbrengen, de stalen staven zullen dan de volledige spanning weerstaan. De verdeling van de drukspanning van het beton wordt nog steeds lineair verondersteld.

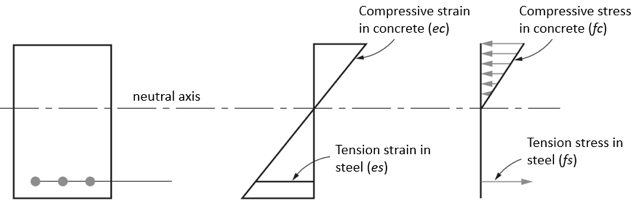
3. Buiggedrag bij ultieme belasting

Hier worden de compressiespanningen en spanningen verhoogd, met enkele niet-lineaire spanningscurven aan de drukzijde van de balk. Deze spanningscurve boven de neutrale as zal in wezen dezelfde vorm hebben als het typische beton spanning-rek curve. Spanning staalspanning fs is gelijk aan vloeispanning van staal fy. Uiteindelijk, de uiteindelijke capaciteit van de straal wordt bereikt en de straal zal falen.

Hierboven beschreven is het eigenlijke mechanisme van het falen van de gewapende betonbalk en is over het algemeen vrij gecompliceerd. Dat is de reden waarom de ontwikkeling van de sterkte-ontwerpbenadering afhankelijk is van de volgende basisaannames:

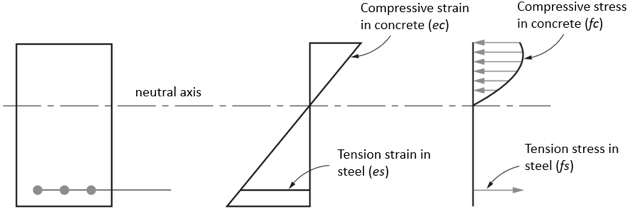
1. Spanning in beton is hetzelfde als in wapeningsstaven op hetzelfde niveau, mits de hechting tussen staal en beton voldoende is;
2. De spanning in beton is lineair evenredig met de afstand tot de neutrale as
3. Vlakke doorsneden blijven vlak na het buigen
4. De treksterkte van beton wordt verwaarloosd
5. Bij een mislukking, Aangenomen wordt dat de maximale rek bij de extreme compressie vezels gelijk is aan beperkt door de ontwerpcode bepaling (0.003)
6. Voor ontwerpkracht, de vorm van de drukverdelingsbetonverdeling kan worden vereenvoudigd.

Veronderstellingen

De bepaling van de momentsterkte is niet eenvoudig vanwege de vorm van het niet-lineaire drukspanningsdiagram boven de neutrale as. Ter vereenvoudiging en praktische toepassing, een fictieve maar gelijkwaardige rechthoekige betonnen spanningsverdeling werd voorgesteld door Whitney en vervolgens overgenomen door de verschillende ontwerpcodes, zoals ACI 318, IN 2, ALS 3600, en anderen. Met betrekking tot deze equivalente spanningsverdeling zoals hieronder weergegeven, de gemiddelde stressintensiteit wordt genomen als fc(bij ultieme belasting) en wordt verondersteld te werken over het bovenste gebied van de dwarsdoorsnede van de balk gedefinieerd door de breedte b en een diepte van a. In verschillende ontwerpcodeparameters, a wordt bepaald door c te verminderen met een factor. Betonsterkte fc wordt ook verminderd. Bijvoorbeeld, volgens de ACI 318 code fc wordt verminderd met 0.85 en een door β1 factor die daartussen ligt 0.65 en 0.85.

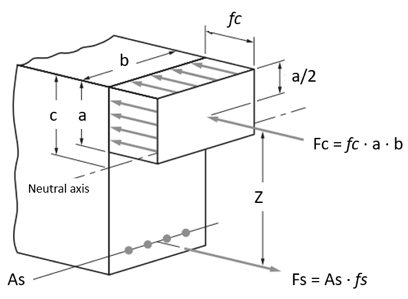
Bereken de diepte van de neutrale as

Om het momentweerstandsvermogen van de sectie van gewapend beton te berekenen, is het nodig om de neutrale asdiepte c correct te berekenen. SkyCiv gebruikt een iteratief proces om de neutrale as te berekenen op basis van het volgende:

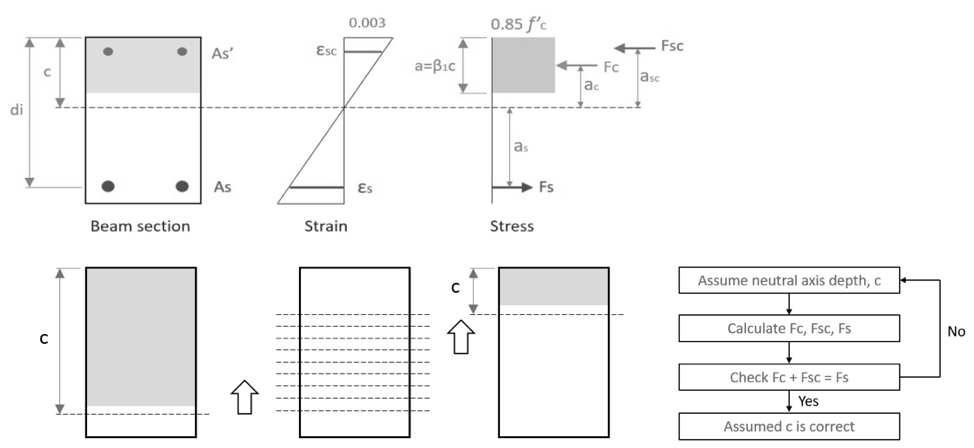
Bereken de Moment Capaciteit

Tenslotte zijn de berekende beton- en staalkrachten Fc, Fs, Fcs en hun positie ten opzichte van de sectie neutrale as a_c, een_s, een_cs laat toe om de ontwerpmomentweerstand te berekenen met de volgende vergelijking:

M_u = F_c ∙ een_c + F_cs ∙ een_cs + F_s ∙ een_s 

Al deze procedure is volledig geautomatiseerd in SkyCiv Versterkte ontwerpsoftware, waar een ingenieur gemakkelijk gewapende betonnen balken kan definiëren met acteren belastingen en bepaal de capaciteit van de sectie. Deze en alle andere berekeningen van de ontwerpcontrole zijn te zien in het gedetailleerde ontwerprapport dat na analyse door SkyCiv wordt gegenereerd.

SkyCiv gewapend beton ontwerp

SkyCiv biedt een volledig uitgeruste Ontwerp van gewapend beton software waarmee u betonnen balk- en betonkolomontwerpen kunt controleren volgens ACI 318, ALS 3600, en EN2 Ontwerpnormen. De software is gebruiksvriendelijk en volledig cloudgebaseerd; vereist geen installatie of downloaden om te beginnen!

Voor meer bundelanalyseoplossingen, bekijk ons SkyCiv Beam – geïntegreerd in de SkyCiv Structurele 3D met het ontwerp van gewapend beton. Of test het nu uit met onze gratis Straaloplosser!

Ga gratis aan de slag