AISC Grondplaat Ontwerp Voorbeeld Amerikaanse Code
Hieronder ziet u een voorbeeld van enkele Amerikaanse basisplaatberekeningen die vaak worden gebruikt bij het ontwerpen van grondplaten:. Stalen voetplaat ontwerp Eurocode, Stalen voetplaat ontwerp Eurocode, Stalen voetplaat ontwerp Eurocode:
- Stalen voetplaat ontwerp Eurocode – over het algemeen gecontroleerd tegen lager- en compressiekrachten met verwijzing naar ACI 318
- Stalen voetplaat ontwerp Eurocode – Stalen voetplaat ontwerp Eurocode, om ervoor te zorgen dat ze voldoende terughoudendheid bieden en niet falen onder stress voor AISC 360
- Stalen voetplaat ontwerp Eurocode – Stalen voetplaat ontwerp Eurocode, zoals hieronder getoond in het voorbeeld ankerboutontwerpberekeningen naar AISC
- Stalen voetplaat ontwerp Eurocode (Kolom) cheques – Stalen voetplaat ontwerp Eurocode
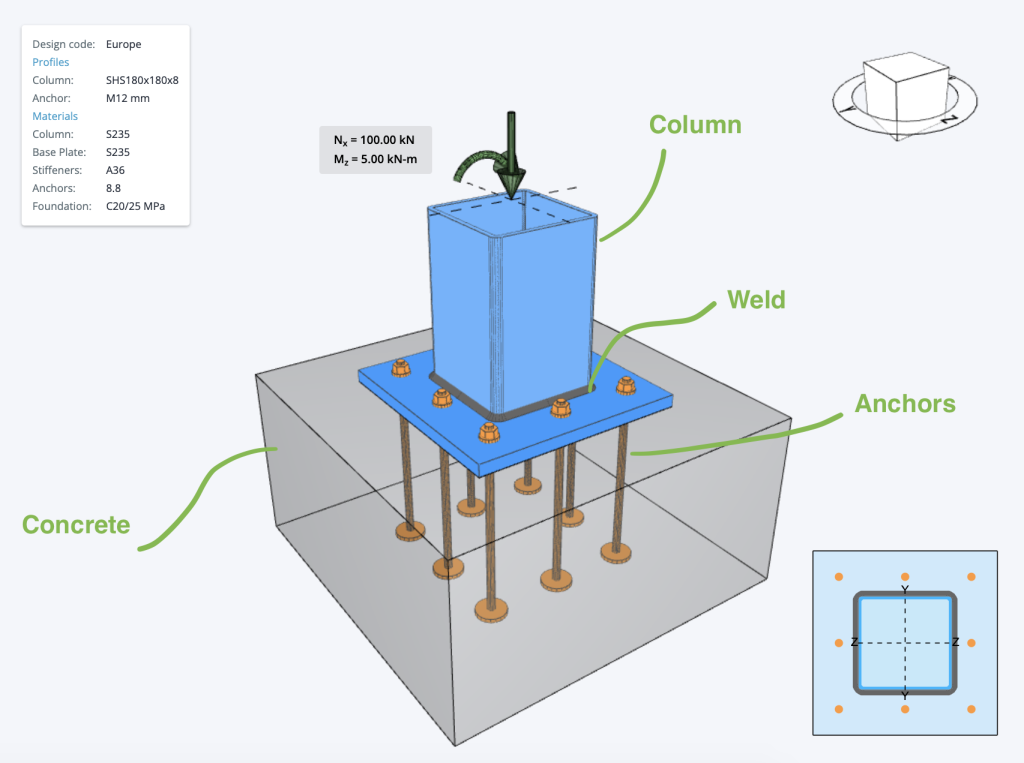
Momenteel, de Stalen bodemplaat ontwerp Stalen voetplaat ontwerp Eurocode. Stalen voetplaat ontwerp Eurocode, Stalen voetplaat ontwerp Eurocode, zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt!
zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt:
Belastingcombinaties:
De Stalen bodemplaat ontwerp het maakt gebruik van factored belastingcombinaties onder ASCE 7-10/16 geldt als volgt::
- \(1.4D)
- \(1.2D + 1.6L + 0.5(L_{r} \tekst{ of } S tekst{ of } R)\)
- \(1.2D + 1.6(Lr tekst{ of } S tekst{ of } R) + (L tekst{ of } 0.5W)\)
- \(1.2D + 1.0W + L + 0.5(Lr tekst{ of } S tekst{ of } R)\)
- \(1.2D + 1.0E + L + 0.2S)
- \(0.9D + 1.0W)
- \(0.9D + 1.0E)
waar :
\(D) = dode belasting
\(L) = live belasting
\(L_{r}\) = dak live belasting
\(S) = Sneeuwbelasting
\(R) = Regenbelasting
\(E) = Aardbeving
\(W) = Windbelasting
zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt:
ACI Beton lagercontrole:
De Stalen bodemplaat ontwerp controleert de betonnen draagkracht (compressie) ontwerp in volgens AISC 360-16 Eq. J8-2.
\( F_{b} = phi _{lager} \keer 0.85 \keer f'_{c} \keren per_{1} \keer sqrt{ \frac{ EEN_{2} }{ EEN_{1} } } \leq F_{b, limiet} = 1.70 \keer f'_{c} \keren per_{1} \)
waar:
\( f'_{c} \) – betondruksterkte
\( EEN_{1} \) – grondplaatgebied in contact met betonoppervlak
\( EEN_{2} \) – betonnen draagvlak
\( \phi_{lager} \) – weerstandsfactor voor beton ( standaardwaarde= 0.65 )
zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt:
AISC Lasontwerpcontrole:
De Stalen bodemplaat ontwerp controleert lasontwerp in overeenstemming met AISC 360-16 J2
\( (ik) R_{n} = R_{nul} + R_{nwt} \)
of
\( (ii) R_{n} = 0,85R_{nul} + 1.5R_{nwt} \)
waar:
\(R_{nul} \) = totale nominale sterkte van langs belaste hoeklassen.
\(R_{nwt} \) = totale nominale sterkte van dwars belaste hoeklassen.
zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt:
ACI-ankerontwerpcontrole:
De Stalen bodemplaat ontwerp controles Ankerparameters zijn van toepassing met behulp van codebepalingen van ACI 318-19 onder hoofdstuk 17.
Ankerstangen zijn ontworpen volgens AISC 360-16 – J9 en ACI 318-19 – Hoofdstuk 17. De volgende weerstanden van ankerbouten worden geëvalueerd::
- Staalsterkte van anker in trek en afschuiving, \( \phi N_{naar} \) en \( \phi V_{naar} \).
- Doorbreeksterkte van beton bij trek en afschuiving, \( \phi N_{cbg} \) en \( \phi V_{cbg} \).
- Uittreksterkte van beton, \( \phi N_{p} \).
- Uitbarstingssterkte van beton aan de zijkant, \( \phi N_{sb} \).
- Beton losbreeksterkte van anker in afschuiving, \( \phi V_{cp} \).
Staalsterkte van anker in trek en afschuiving
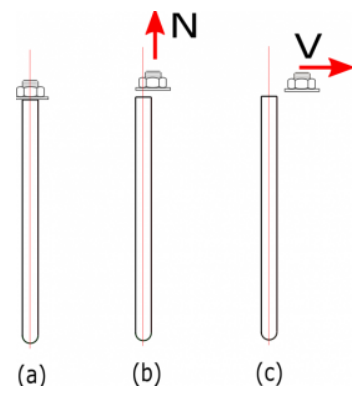
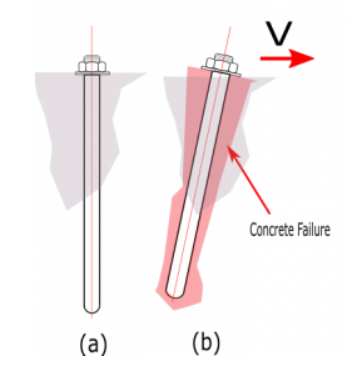
Afbeelding A. (een) onbreekbare bout (b) boutuitbraak als gevolg van spanningsfout (c) bout uitsplitsing door afschuiffout
Factored staalsterkte van anker in trek en afschuiving wordt bepaald volgens ACI 318-19 - 17.6.1.2 en 17.7.1 net zo
voor spanning
\( \phi _{spanning, anc} N_{naar} = phi _{spanning, anc} EEN_{ik weet,N}f_{uta} \rechter pijl \) vergelijking 17.6.1.2
voor scheren
\( \phi _{schuintrekken, anc} V_{naar} = phi _{schuintrekken, anc} 0.6EEN_{ik weet,V }f_{uta} \rechter pijl \) vergelijking 17.7.1.2b
waar:
- \( \phi _{spanning, anc} \) – sterktereductiefactor voor ankers in trek ( standaardwaarde = 0.75 )
- \( \phi _{schuintrekken, anc}\) – sterktereductiefactor voor ankers in afschuiving ( standaardwaarde = 0.65 )
- \( EEN_{ik weet,N}\) – is het effectieve dwarsdoorsnede-oppervlak van een anker onder spanning.
- \( EEN_{ik weet,V }\) – is de effectieve dwarsdoorsnede van een anker onder afschuiving.
- \( f_{uta}\) – gespecificeerde treksterkte van ankerstaal en mag niet groter zijn dan \(1.9f_{Ja}\) en 125 KSI (861.845 Mpa)
Doorbraaksterkte van beton
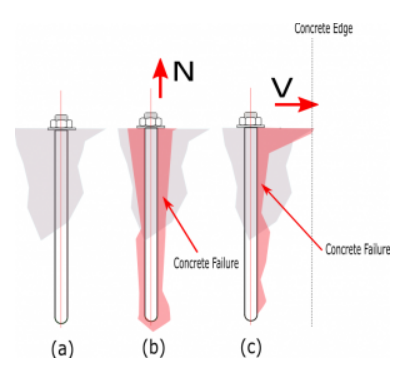
Figuur B. (een) Boutsteun op beton (b) betondoorbraak door spankracht (c) betondoorbraak door afschuifkracht
Factored doorbreeksterkte van beton van anker in trek en afschuiving wordt bepaald volgens ACI 318-19 - 17.6.2 en 17.7.1 net zo
\( \phi N_{cbg} = phi frac{ EEN_{Nc} }{ EEN_{Onthouden} } \psi_{eg,N} \psi_{ed,N} \psi_{c,N} \psi_{cp,N} N_{b} \rechter pijl \) vergelijking 17.6.2.ab
waar:
\( \phi \) – sterktereductiefactor voor ankers in trek ( standaardwaarde = 0.75 ).
\( EEN_{Nc} \) – geprojecteerd betonfalen van een enkele of groepsankers.
\( EEN_{Onthouden} \)- project beton faalgebied van een enkel anker, voor berekening van treksterkte indien niet beperkt door randafstand of afstand distance.
\( \psi_{eg,N} \) – Breakout-excentriciteitsfactor in spanning.
\( \psi_{eg,N} = frac{1.00}{ 1 + \frac{e^{‘}_{N}}{1.5 h_{ef}} } \leq 1.00 \rechter pijl \) vergelijking 17.6.2.3.1
\( \psi_{ed,N} \) – Breakout-effectfactor bij spanning.
(een) \( \tekst{als } C_{een,min} \geq 1.5h_{ef} \tekst{ vervolgens } \psi_{ed,N} = 1.00 \) vergelijking 17.6.2.4.1a
en
(b) \( \tekst{als } C_{een,min} < 1.5h_{ef} \tekst{ vervolgens } \psi_{ed,N} = 0.70 + 0.3\frac{C_{een,min}}{1.5h_{ef}} \) vergelijking 17.6.2.4.1b
\( \psi_{c,N} \) – Breakout cracking factor in spanning.
\( \psi_{c,N} = 1.25 \) voor ingestorte ankers
\( \psi_{cp,N} \) – Breakout splitsfactor in spanning.
(een) \( \tekst{als } C_{een,min} \geq C_{ac} \tekst{ vervolgens } \psi_{cp,N} = 1.00 \) vergelijking 17.6.2.4.1a
en
(b) \( \tekst{als } C_{een,min} < C_{ac} \tekst{ vervolgens } \psi_{cp,N} = frac{ C_{een,min} }{ C_{ac}} \geq frac{ 1.5h_{ef} }{ C_{ac} } \) vergelijking 17.6.2.4.1b
\( N_{b} \) – basisuitbreeksterkte van beton in trek van een enkel anker in gescheurd beton.
Uittreksterkte van beton
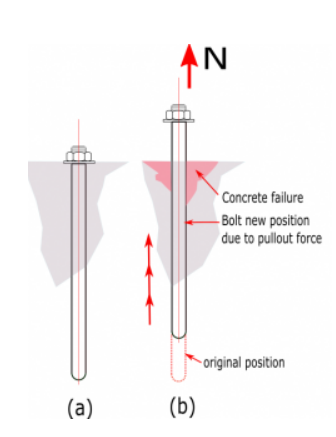
Figuur C. (een) Boutsteun op beton (b) bout lostrekken van beton als gevolg van trekkracht
De uittreksterkte van beton in factoren van een anker wordt gedefinieerd in ACI 318-19 - 17.6.3 net zo
Npn = φΨc,P. Np
waar:
\( \phi \) – sterktereductiefactor voor ankers in trek ( standaardwaarde = 0.70 ).
\( \psi_{c, P.} \) – wijzigingsfactor voor concrete toestand
Voor gescheurd beton:
\( \psi_{c, P.} \) = 1.0
Voor ongescheurd beton:
\( \psi_{c, P.} \) = 1.4
\( N_{p} \) – Uittreksterkte anker
Voor gescheurd beton:
\( N_{p} = 8A_{brg}f^{‘}_{c}\) vergelijking 17.6.3.2.2a
Voor ongescheurd beton:
\( N_{p} = 0.9f^{‘}_{c}e_{h}d_{een} \rechter pijl \) vergelijking 17.6.2.2.b
waar \( 3d_{een} \leq e_{h} \niveau 4.5d_{een} \)
\( f^{‘}_{c} \) – gespecificeerde druksterkte van beton.
\( EEN_{brg} \) – netto dragend gebied van de kop van de stift, ankerbout of vervormde staaf met kop.
\( e_{h} \) – afstand van het binnenoppervlak van de schacht van een J-bout of L-bout tot de buitenste punt van de J- of L-bout.
\( d_{een} \) – buitendiameter van anker of schachtdiameter van kopbout stu, kopbout, of haakbout.
Uitbarstingssterkte van beton aan de zijkant
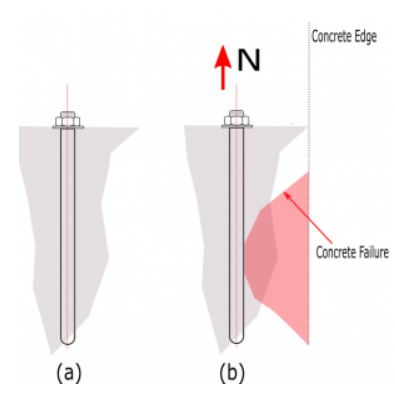
Figuur D. (een) Boutsteun op beton (b) bout met betonfout (Side-blow) dichtbij de rand tot spankracht
De sterkte van de uitbarsting van een anker aan de zijkant van een anker wordt gedefinieerd in ACI 318-19 - 17.6.4 net zo
\( \phi N_{sb} = 160C_{a1}\sqrt{EEN_{brg}}\lambda _{een} \sqrt{f^{‘}_{c} } \rechter pijl \) vergelijking 17.6.4.1
waar:
\( f^{‘}_{c} \) – gespecificeerde druksterkte van beton.
\( EEN_{brg} \) – netto dragend gebied van de kop van de stift, ankerbout of vervormde staaf met kop.
\( \lambda_{een} \) – modificatiefactor om de verminderde mechanische eigenschappen van lichtgewicht beton in bepaalde betonverankeringstoepassingen weer te geven.
Concrete uitbreeksterkte van anker