Fundering is een essentieel element van een constructie om algehele stabiliteit te bieden door de totale belastingen van de constructie naar de grond over te brengen en te verdelen. Ondiepe fundamenten, zoals rechthoekige of vierkante geïsoleerde voet, zijn het geprefereerde type fundering vanwege de eenvoud van hun constructie en totale kosten in vergelijking met diepe funderingen. Het schatten van de basisdruk heeft een dramatische invloed op het ontwerp en de maatvoering van de fundering. Typisch, de nutsverhouding tussen het toelaatbare draagvermogen van de grond en de heersende basisdruk onder de fundering is de basis van de initiële grootte van de fundering. Zodra de initiële afmetingen van de fundering zijn ingesteld, verdere ontwerpcontroles op veiligheid en stabiliteit, zoals eenrichtings- en tweerichtingsschaar, buigcapaciteit:, en ontwikkelingslengtecontroles, worden gecontroleerd afhankelijk van welke ontwerpcode wordt gebruikt.
Wanneer een voet wordt onderworpen aan een bi-axiale buiging (MX, Mz), er wordt aangenomen dat de axiale belasting (P.) werkt op een excentriciteitscoördinaat (eX, ez) waar de neiging bestaat om vanuit het midden te roteren. De interactie tussen grond en fundering hangt voornamelijk af van de afmeting van de fundering en de resulterende excentriciteit van de uitgeoefende belastingen. Afhankelijk van de locatie van de resulterende excentriciteit, de basisdruk zorgt ervoor dat de voet volledig of gedeeltelijk wordt samengedrukt. In praktijk, het wordt aanbevolen om een voet met volledige compressie te ontwerpen. Gedeeltelijke compressie of verlies van contact tussen de grond en de fundering mag niet worden verwaarloosd, maar de meeste ontwerpers vermijden dit scenario vanwege de complexiteit van de berekening. De fundering is in volledige compressie wanneer de resulterende excentriciteit zich binnen de kern of onder Zone C . bevindt. Excentriciteit buiten Zone C zet de voet in gedeeltelijke compressie. Figuur 1 toont de verschillende aangewezen zones op een rechthoekige basis.
Dit artikel richt zich op het berekenen van hoekdruk onder verschillende zoneclassificaties op basis van Bellos & Spoor (2017) en S.S. Ray's (1995) studeert.
Zoneclassificaties van een rechthoekige voet
De zoneclassificaties van een rechthoekige voet zijn afgeleid van meerdere onderzoeken door verschillende auteurs om een praktische benadering te ontwikkelen voor het schatten van de verdeling van de bodemdruk onder verwachte belastingsomstandigheden. Zoals te zien in figuur 1, er zijn vijf verschillende regio's (Zones A-E) afhankelijk van de locatie van de resulterende excentriciteit. Elke zone komt overeen met een andere belasting, basis drukverdeling:, en vervorming. Zone C, ook bekend als de kern, is de belangrijkste kern. Het is de ideale regio om voet aan de grond te krijgen, resulterend in volledige compressie op de voet. De afmetingen van dit gebied zijn gelijk aan: 1/6 van zijn respectieve voetlengte.

Figuur 1: Zoneclassificaties van een rechthoekige voet
De secundaire kern is het elliptische gebied (begrensd door de stippellijn in Afbeelding 1) met zijn grote en kleine halve assen gelijk aan 1/3 van zijn respectieve voetlengte. Deze regio beslaat de hele zones B & C en sommige delen van zones D & E. Secundaire kern resulteert in een gedeeltelijke compressie van de voet. Het is een goede gewoonte om de excentriciteit binnen de secundaire zone te handhaven voor een acceptabel ontwerp van de fundering.
Excentriciteit buiten de secundaire zone is het resultaat van hoge biaxiale belasting. Het bestrijkt de gehele zone A en de overige delen van zones D & E. Het wordt aanbevolen om het ontwerp van de voet in deze regio's te vermijden, omdat het risico bestaat dat deze omvalt. Vandaar, het is raadzaam om de voetafmetingen voor dit type lading opnieuw te ontwerpen.
Het volgende somt de analytische formules op voor het oplossen van de hoekdrukken in elke zoneclassificatie:.
Zone C (belangrijkste kern:, Volledige compressiezone)
Zoals genoemd, dit is het meest geprefereerde geval voor het ontwerpen van funderingen, aangezien het in staat is om de hele basis van de fundering in compressie te brengen, zoals te zien in figuur 2. Dit geval wordt weergegeven door kleine excentriciteit binnen de kern of geen excentriciteit. Figuur 2 toont de excentriciteit binnen de kern met zijn maximale druk op de hoeken P3 & P4 en minimale druk op hoeken P1 & Een overzicht van de berekeningen die nodig zijn om een gecombineerde fundering te ontwerpen.

Figuur 2: Excentriciteit (-eX, -ez) in zone C & volledig compressiegebied
Maximaal & minimale hoekdruk (mooi & Spoor, 2017):


| Hoekdruk gebaseerd op excentriciteit | ||||
|---|---|---|---|---|
| P.1 | P.2 | P.3 | P.4 | |
| +eX, +ez | P.max | P.max | P.min | P.min |
| +eX, -ez | P.max | P.max | P.min | P.min |
| -eX, -ez | P.min | P.min | P.max | P.max |
| -eX, +ez | P.min | P.min | P.max | P.max |
Zone A (Driehoekige compressiezone)
Dit geval komt overeen met vier rechthoekige gebieden in elke hoek van de voet. Het komt meestal voor met grote bi-axiale excentriciteit, het opleggen van een hoog driehoekig drukgebied in een van de hoeken, zoals weergegeven door het gearceerde gebied in figuur 3. De overige hoeken verliezen het contact met de grond. Vandaar, dit geval is niet aan te raden voor ontwerp.
 Figuur 3: Excentriciteit (-eX, -ez) in zone A & driehoekig compressiegebied rond P3
Figuur 3: Excentriciteit (-eX, -ez) in zone A & driehoekig compressiegebied rond P3
Aanbevolen veiligheidsfactor voor lagers: (mooi & Spoor, 2017):

| Hoekdruk gebaseerd op excentriciteit | ||||
|---|---|---|---|---|
| P.1 | P.2 | P.3 | P.4 | |
| eX(+), ez(+) | P.max | 0 | 0 | 0 |
| eX(+), ez(-) | 0 | P.max | 0 | 0 |
| eX(-), ez(-) | 0 | 0 | P.max | 0 |
| eX(-), ez(+) | 0 | 0 | 0 | P.max |
Zone D (Trapeziumvormige compressiezone)
Zone D komt ook overeen met grote excentriciteiten in de gebieden die in de x-richting van de fundering zijn bevestigd, zoals te zien in figuur 4. De excentriciteit in de z-richting (ez) is veel groter dan in de x-richting (eX). In dit geval, twee hoeken van de voet verliezen het contact met de grond en produceren een trapeziumvormig drukgebied. Vergeleken met zone A, die geheel buiten de secundaire zone ligt, een deel van zone D valt nog onder de secundaire zone.

Figuur 4: Excentriciteit (-eX, -ez) in zone D & trapeziumvormig compressiegebied rond P3
Maximaal & minimale hoekdruk (mooi & Spoor, 2017):


Verticale hoogten van het trapeziumvormige drukgebied (mooi & Spoor, 2017):


| Hoekdruk gebaseerd op excentriciteit | ||||
|---|---|---|---|---|
| P.1 | P.2 | P.3 | P.4 | |
| eX(+), ez(+) | P.max | 0 | 0 | P.min |
| eX(+), ez(-) | 0 | P.max | P.min | 0 |
| eX(-), ez(-) | 0 | P.min | P.max | 0 |
| eX(-), ez(+) | P.min | 0 | 0 | P.max |
Zone E (Trapeziumvormige compressiezone)
Vergelijkbaar met zone D, dit geval produceert ook een trapeziumvormig drukgebied maar wordt veroorzaakt door een grote excentriciteit in de x-richting(eX).
 Figuur 5: Excentriciteit (-eX, -ez) in zone E & trapeziumvormig compressiegebied rond P3
Figuur 5: Excentriciteit (-eX, -ez) in zone E & trapeziumvormig compressiegebied rond P3
Maximaal & minimale hoekdruk (mooi & Spoor, 2017):


Horizontale bases van het trapeziumvormige drukgebied (mooi & Spoor, 2017):


| Hoekdruk gebaseerd op excentriciteit | ||||
|---|---|---|---|---|
| P.1 | P.2 | P.3 | P.4 | |
| eX(+), ez(+) | P.max | P.min | 0 | 0 |
| eX(+), ez(-) | P.min | P.max | 0 | 0 |
| eX(-), ez(-) | 0 | 0 | P.max | P.min |
| eX(-), ez(+) | 0 | 0 | P.min | P.max |
Zone B (Vijfhoekige compressiezone)
Dit geval doet zich voor wanneer de uitgeoefende belastingen op de fundering een matige excentriciteit genereren binnen de secundaire zone. De gebieden die onder zone B vallen, worden begrensd door twee gebogen zijden en een vlakke basis rond de buitenkant van zone C. In dit geval, er ontstaat een vijfhoekig drukgebied, en slechts een hoek van de voet verliest het contact met de grond. Echter, de onderstaande oplossingen zijn enigszins ingewikkeld en vereisen numerieke oplossingsmethoden voor de hoekdrukken en de x & y intercepts van het compressiegebied.

Hoekschoppen (mooi & Spoor, 2017):


Vijfhoekige zijden van het drukgebied (mooi & Spoor, 2017):



| Hoekdruk gebaseerd op excentriciteit | ||||
|---|---|---|---|---|
| P.1 | P.2 | P.3 | P.4 | |
| eX(+), ez(+) | P.max | P.q | 0 | P.p |
| eX(+), ez(-) | P.p | P.max | P.q | 0 |
| eX(-), ez(-) | 0 | P.p | P.max | P.q |
| eX(-), ez(+) | P.q | 0 | P.p | P.max |
Alternatief, een meer directe oplossing door S.S. straal (1995) kan worden gebruikt voor de hoekdrukken en onderscheppingen van de vijfhoekige drukzone. De vergelijkingen worden hieronder gegeven:

Hoekschoppen (SS. straal, 1995):



Vijfhoekige zijden van het drukgebied (SS. straal, 1995):


SkyCiv's Module voor funderingsontwerp is in staat om de basisdrukken van een rechthoekige betonnen voet op te lossen. Aanvullende ontwerpcontroles in overeenstemming met verschillende ontwerpcodes (ACI 318-14, Australische standaard 2009 & 2018, Eurocode, en Canadese normen) zijn ook beschikbaar.
Laatste update
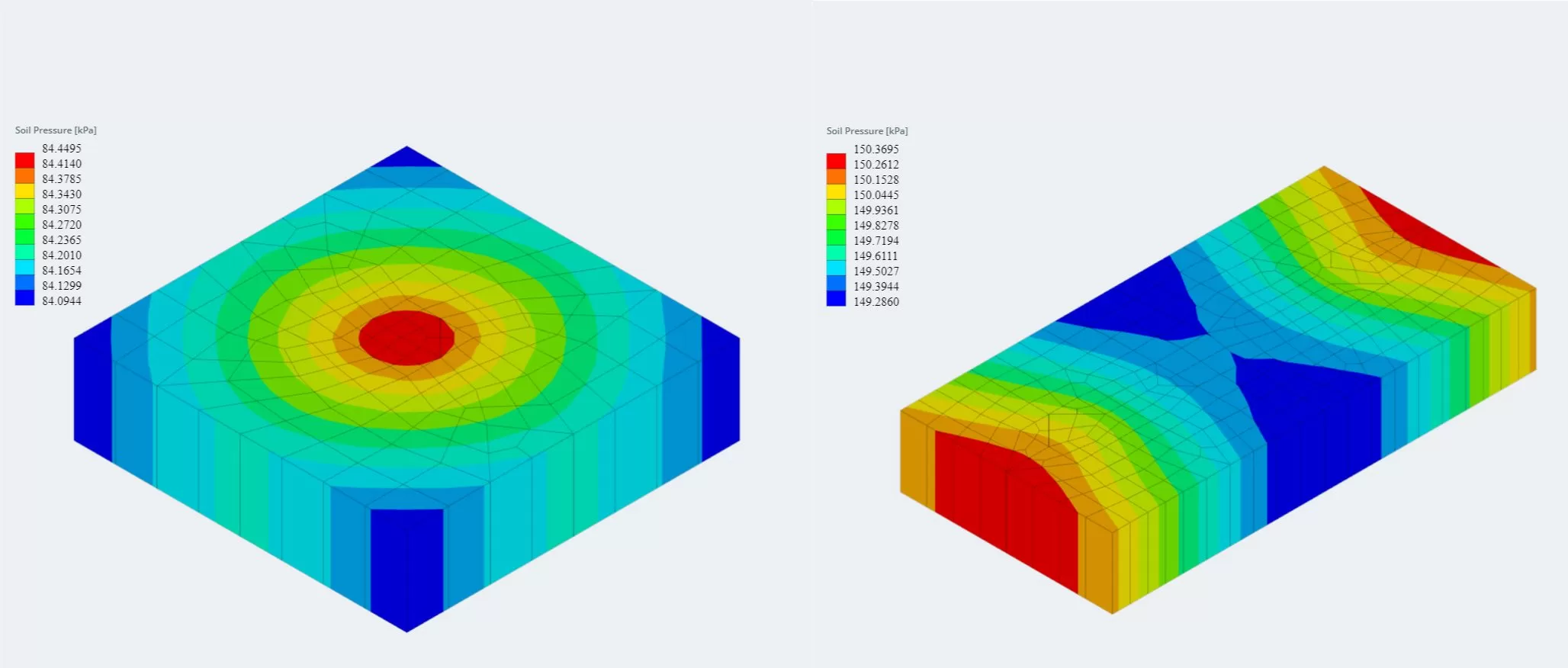
De nieuwste versie van de funderingsmodule is nu geïntegreerd met Eindige Elementenanalyse (LELIJK), die een krachtigere analyse van de bodemdruk biedt en een analyse van houtbewapening introduceert die kan worden gebruikt voor een veel gedetailleerdere buigcontrole. FEA-resultaten voor de bodemdruk en houtbewapeningsmomenten zijn in 3D te bekijken en toegevoegd aan de rapportages.
Wil je de Foundation Design-software van SkyCiv proberen?? Met onze gratis tool kunnen gebruikers presteren betonfunderingsberekeningen zonder enige download of installatie!
Referenties:
- mooi, J., Spoor, N. (2017). Complete analytische oplossing voor lineaire bodemdrukverdeling onder stijve rechthoekige spreidvoeten.
- De, B.M. (2007). Principes van funderingstechniek (7e editie). Wereldwijde engineering
- Rawat, S., et. al. (2020). Geïsoleerde rechthoekige funderingen onder biaxiale buiging: Een kritische beoordeling en vereenvoudigde analysemethodologie.
- straal, SS. (1995). Gewapend beton. Blackwell-wetenschap
Productontwikkelaar
BSc (Civiel), MSc (Civiel)



