- Definitie van Balkdoorbuiging
- Eenheid van Balkdoorbuiging
- Vergelijkingen/Formules voor Balkdoorbuiging
- Voorbeeld Berekening van Doorbuiging voor Eenvoudig Ondersteunde Balk
1. Definitie van Balkdoorbuiging
Wat is doorbuiging? Doorbuiging, in termen van constructieve engineering, verwijst naar de verplaatsing van een balk of knooppunt vanuit zijn oorspronkelijke positie als gevolg van de krachten en belastingen die op het element worden uitgeoefend. Het wordt ook wel verplaatsing genoemd en kan optreden door extern aangebrachte belastingen, door het gewicht van de constructie zelf en door de zwaartekracht die hierop werkt.
Doorbuiging kan optreden in balken, vakwerken, frames, en in feite elke andere constructie. Om doorbuiging te definiëren, laten we een eenvoudige doorbuiging van een uitkragende balk nemen waarbij iemand met gewicht (W) aan het uiteinde staat:

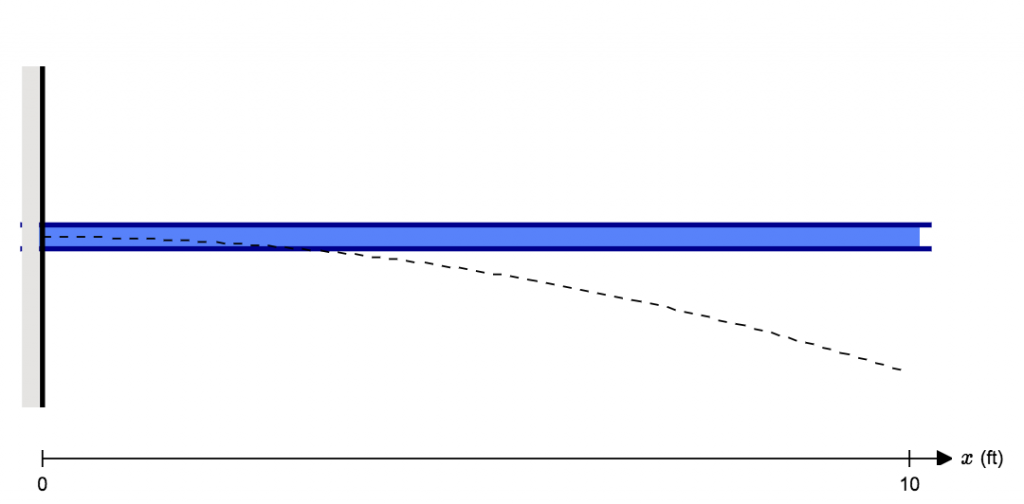
De kracht van deze persoon die aan het uiteinde staat, zal ervoor zorgen dat de balk buigt en afwijkt van zijn natuurlijke positie. In het onderstaande diagram, is de blauwe balk de oorspronkelijke positie, en de stippellijn simuleert de doorbuiging van de uitkragende balk:
Zoals je kunt zien, is de balk gebogen of verplaatst vanaf de oorspronkelijke positie. Deze afstand op elk punt langs het element is de betekenis of definitie van doorbuiging.
Er zijn over het algemeen 4 hoofdvariabelen die bepalen hoeveel een balk doorbuigt. Deze omvatten:
- Hoeveel belasting er op de constructie rust
- De lengte van het onondersteunde deel
- Het materiaal, specifiek de Elasticiteitsmodulus
- De doorsnede-afmetingen, specifiek het traagheidsmoment (I)
2. Eenheid van Balkdoorbuiging
De eenheid van doorbuiging, of verplaatsing, s een lengteenheid en wordt normaal gesproken genomen als mm (voor metrisch) en inch (voor imperial). Dit getal definieert de afstand waarmee de balk is doorgebogen vanuit de oorspronkelijke positie. Aangezien doorbuiging een korte afstandsmeting is (balken mogen over het algemeen slechts in kleine hoeveelheden doorbuigen), wordt het vaak uitgedrukt in lengteenheden, zoals inches of millimeters.
Naast dit, daarnaast zijn er andere parameters om doorbuiging te meten, zoals hoeken, maar deze eenheden zoals radialen of graden worden niet vaak gebruikt. Bovendien, het is ook belangrijk op te merken dat de toegestane doorbuiging voor een constructie vaak wordt gespecificeerd als een percentage van de overspanningslengte (L/X), dit is een maatstaf die vergelijking tussen verschillende balken mogelijk maakt ongeacht hun lengte en is eenheidloos.
3. Vergelijkingen/Formules voor Balkdoorbuiging
De vergelijkingen zijn eenvoudig toe te passen en stellen ingenieurs in staat om snel en eenvoudig doorbuigingsberekeningen te maken. Als je niet zeker weet wat doorbuiging precies is, klik hier voor een definitie van doorbuiging Hieronder staat een beknopte tabel die laat zien hoe je de maximale doorbuiging in een balk kunt berekenen. Geen zin om deze handmatig te berekenen? SkyCiv biedt een gratis balkdoorbuigingscalculator om je te helpen! Voor krachtigere structurele analyse software, meld je aan voor een gratis SkyCiv-account en krijg direct toegang tot alle gratis versies van onze cloud structurele analysesoftware!
Gebruik de onderstaande formule om de maximale verplaatsing in balken te berekenen. Klik op de 'check answer' knop om onze gratis balkcalculator. Deze balkverplaatsingsvergelijkingen zijn perfect voor snelle handberekeningen en snelle ontwerpen.
De doorbuiging van een balk wordt berekend op basis van verschillende factoren, waaronder materialen, het traagheidsmoment van een sectie, de aangebrachte kracht, en de afstand tot de steun. Deze kunnen worden vereenvoudigd in eenvoudige doorbuigingsformules voor snelle berekeningen. Hier is een eenvoudige tabel met de verschillende belastingscenario's en hun bijbehorende maximale balkdoorbuigingsformules:
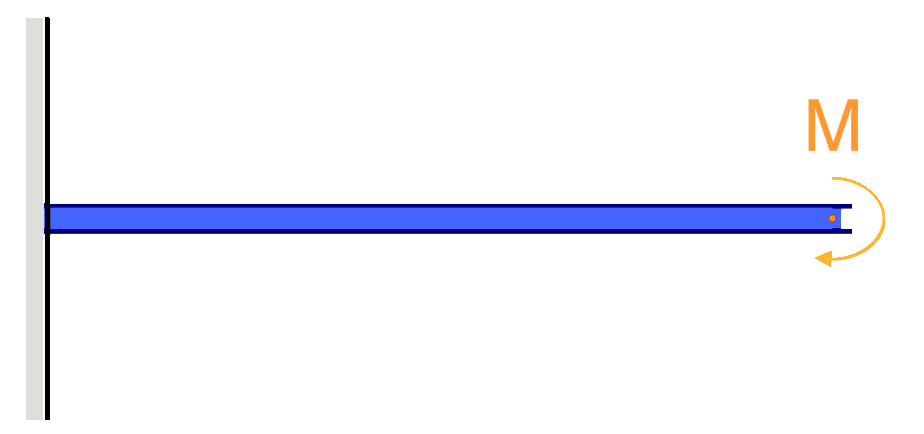
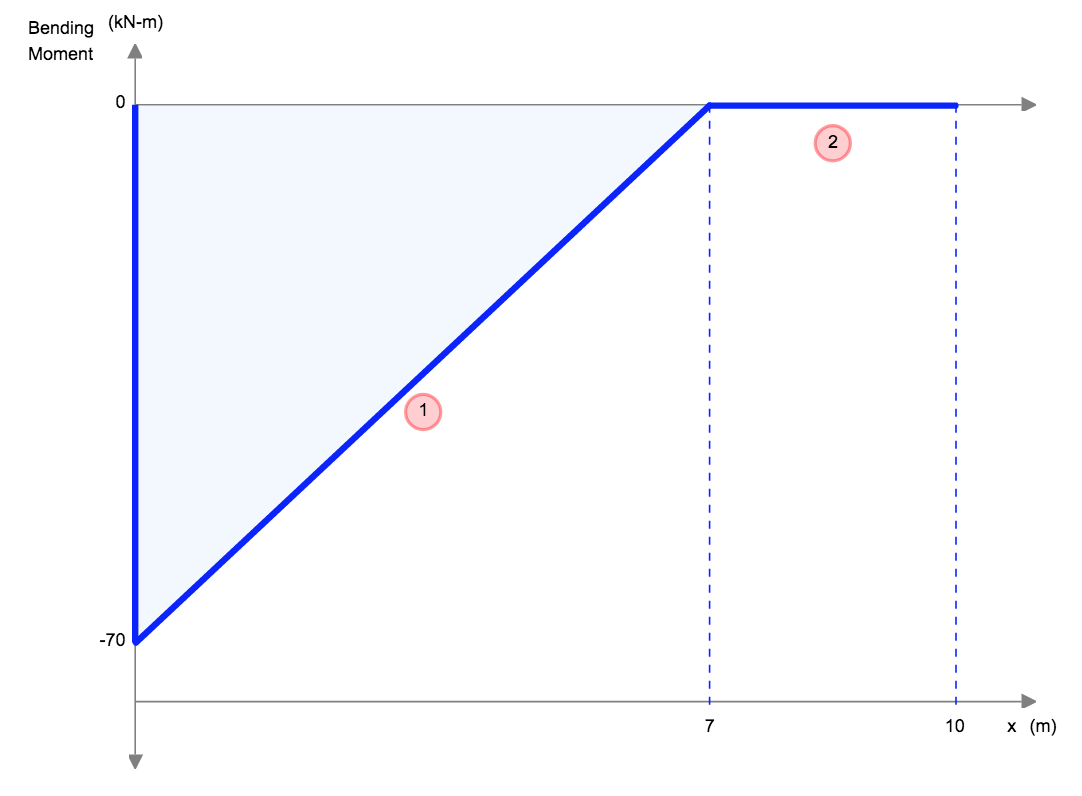
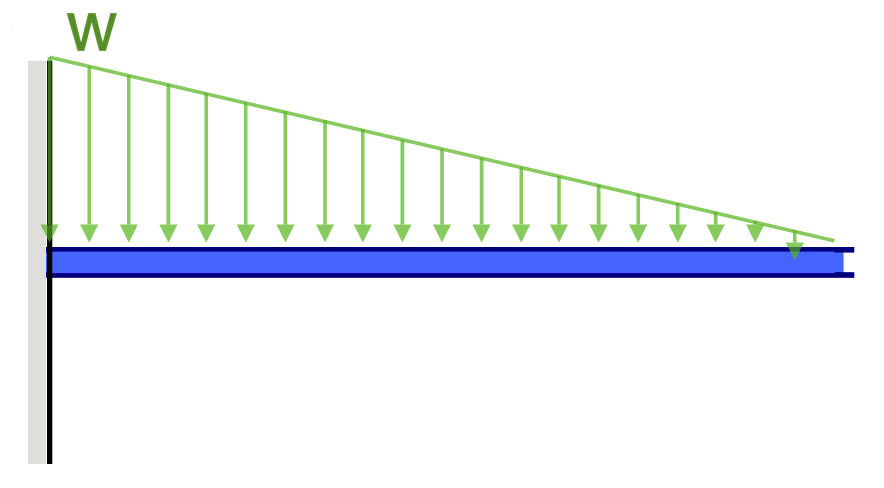
Doorbuigingsvergelijkingen/Formules voor Uitkragende Balk
Uitkragende balken zijn speciale soorten balken die slechts door één steunpunt worden ondersteund, zoals te zien is in het bovenstaande voorbeeld. Deze elementen zouden van nature meer doorbuigen omdat ze slechts aan één uiteinde worden ondersteund.
Het is belangrijk om te overwegen dat de doorbuiging van een uitkragende balk ook wordt beïnvloed door de positie van de belasting en de locatie van de vaste steun. Hoe verder de belasting van de vaste steun af is, hoe groter de doorbuiging zal zijn. En, hoe langer de uitkraging, hoe groter de doorbuiging zal zijn, omdat de belasting op een langere afstand wordt uitgeoefend.
Het is ook belangrijk op te merken dat er een maximale toegestane doorbuiging voor constructies is, deze waarde wordt meestal vastgesteld door bouwvoorschriften en normen, het varieert met het type constructie en het doel van de constructie, en de berekende doorbuiging moet binnen deze limiet liggen om de veiligheid en functionaliteit van de constructie te waarborgen.
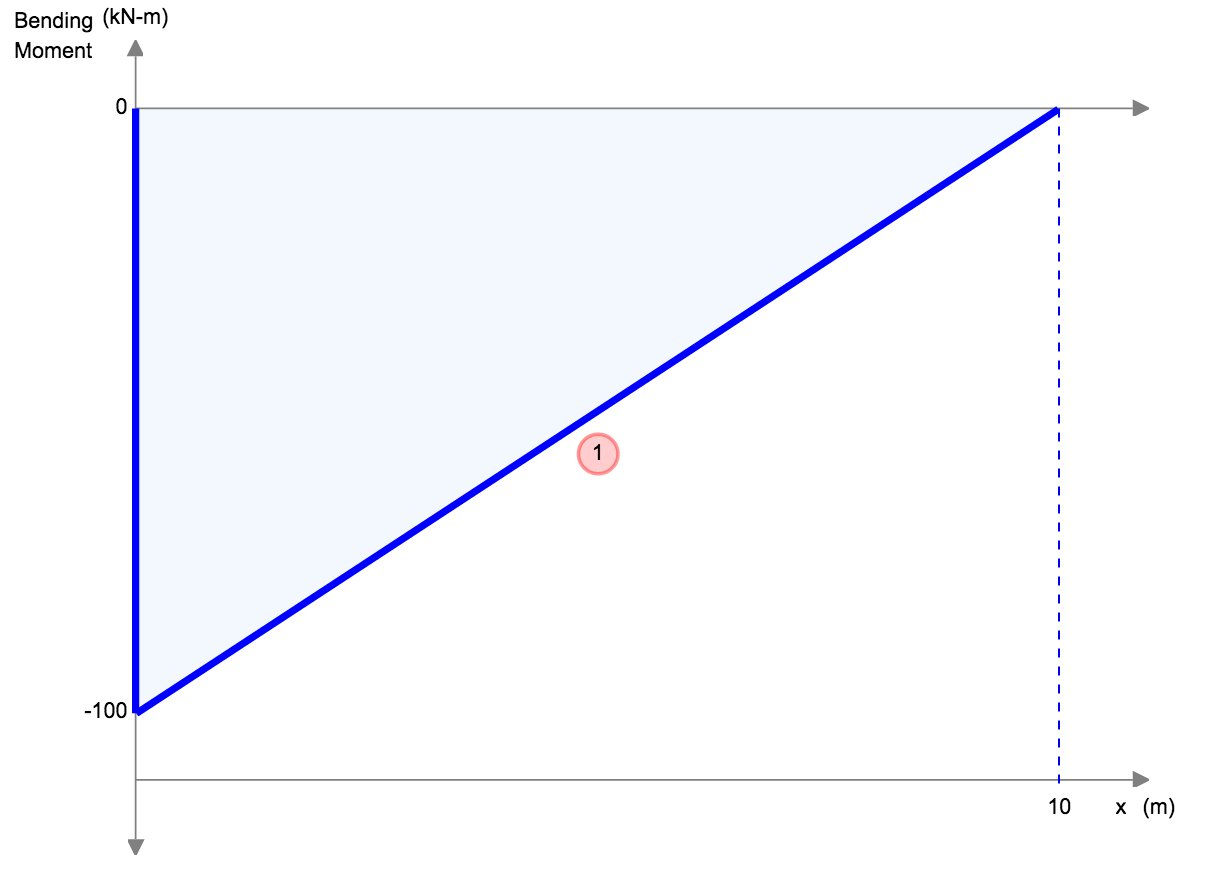
| Referentie | Max doorbuiging | BMD-vorm |
 |
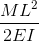 |
 |
 |
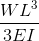 |
 |
 |
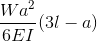 |
 |
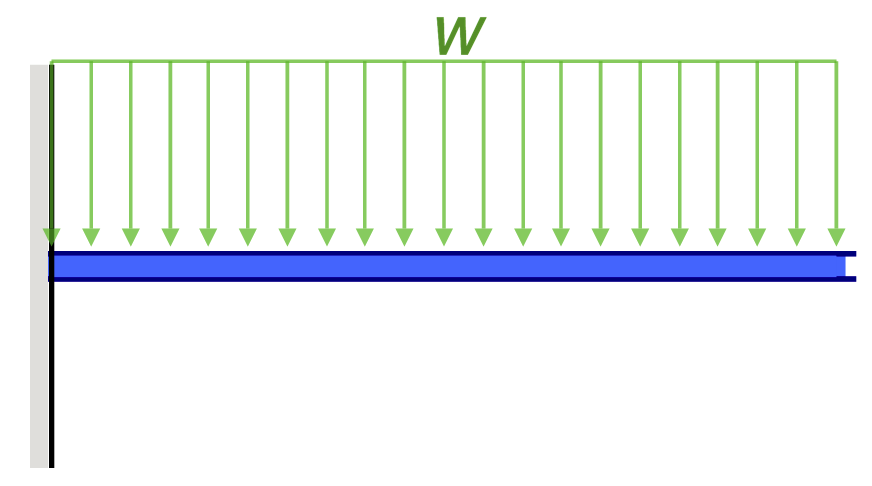
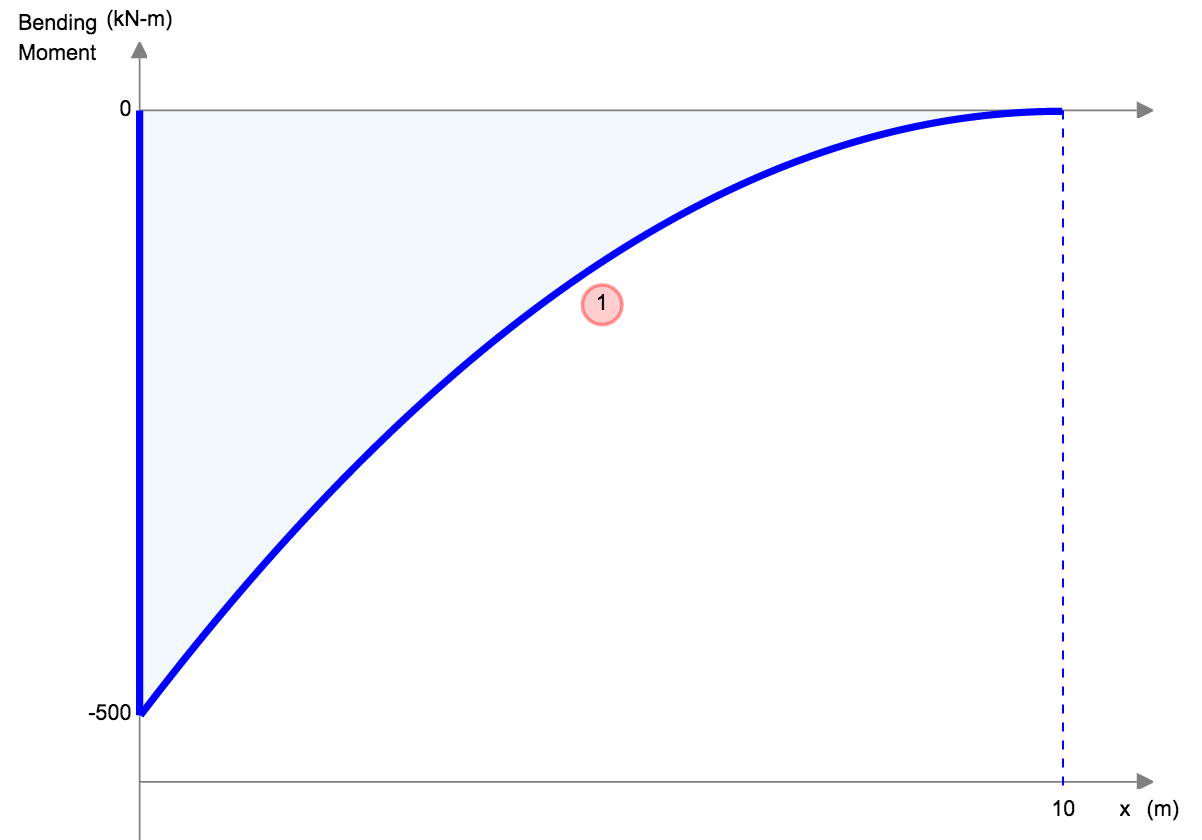
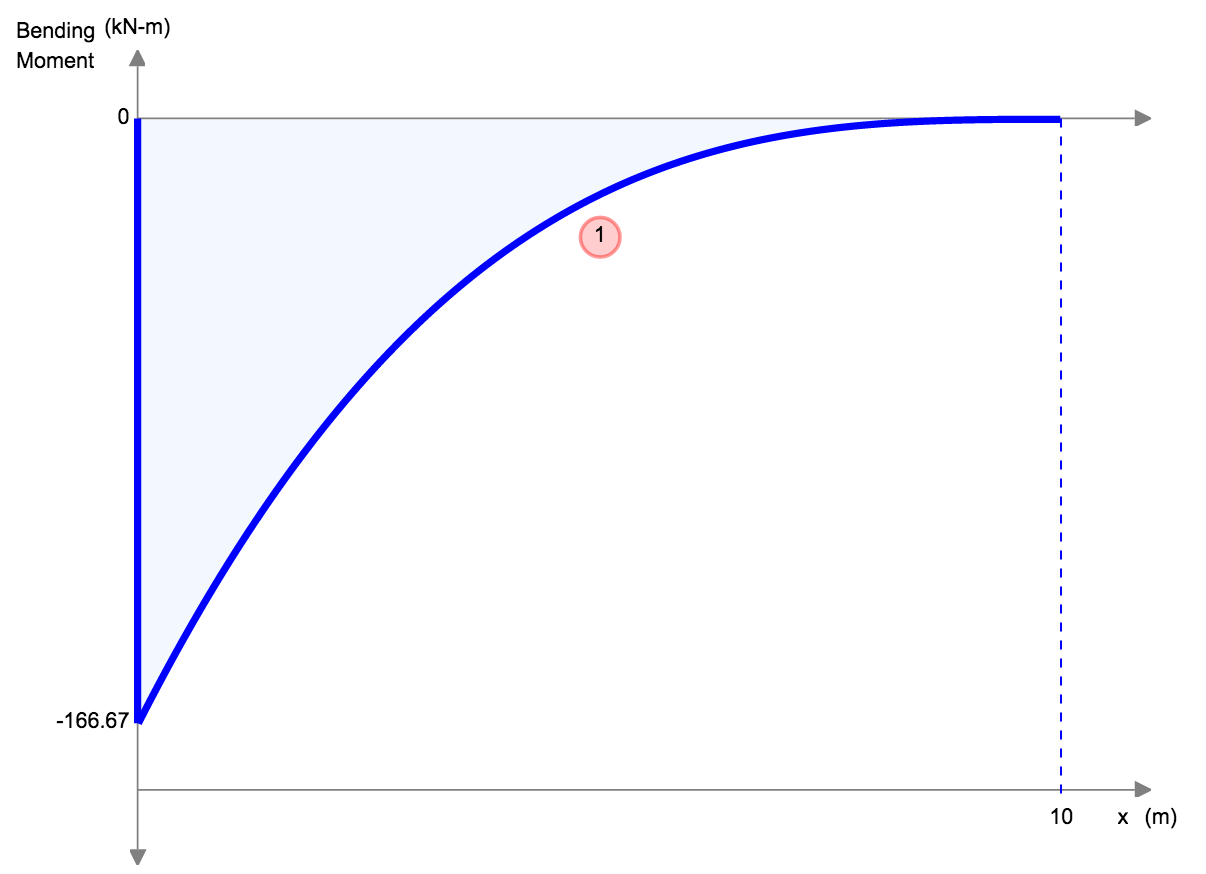
Doorbuigingsvergelijkingen/Formules voor Eenvoudig Ondersteunde Balk
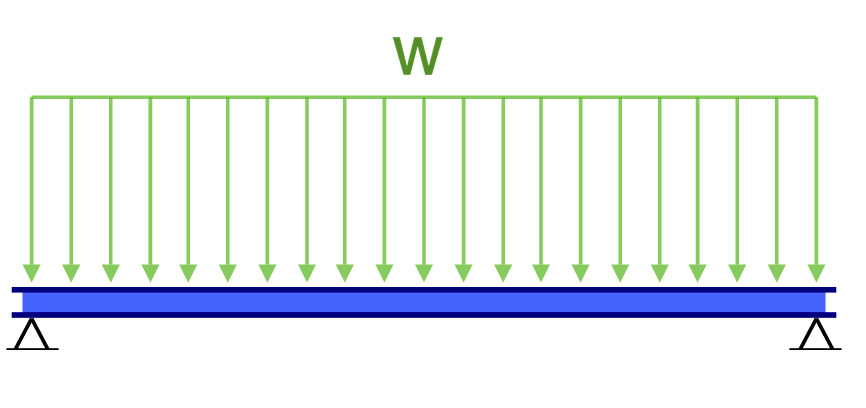
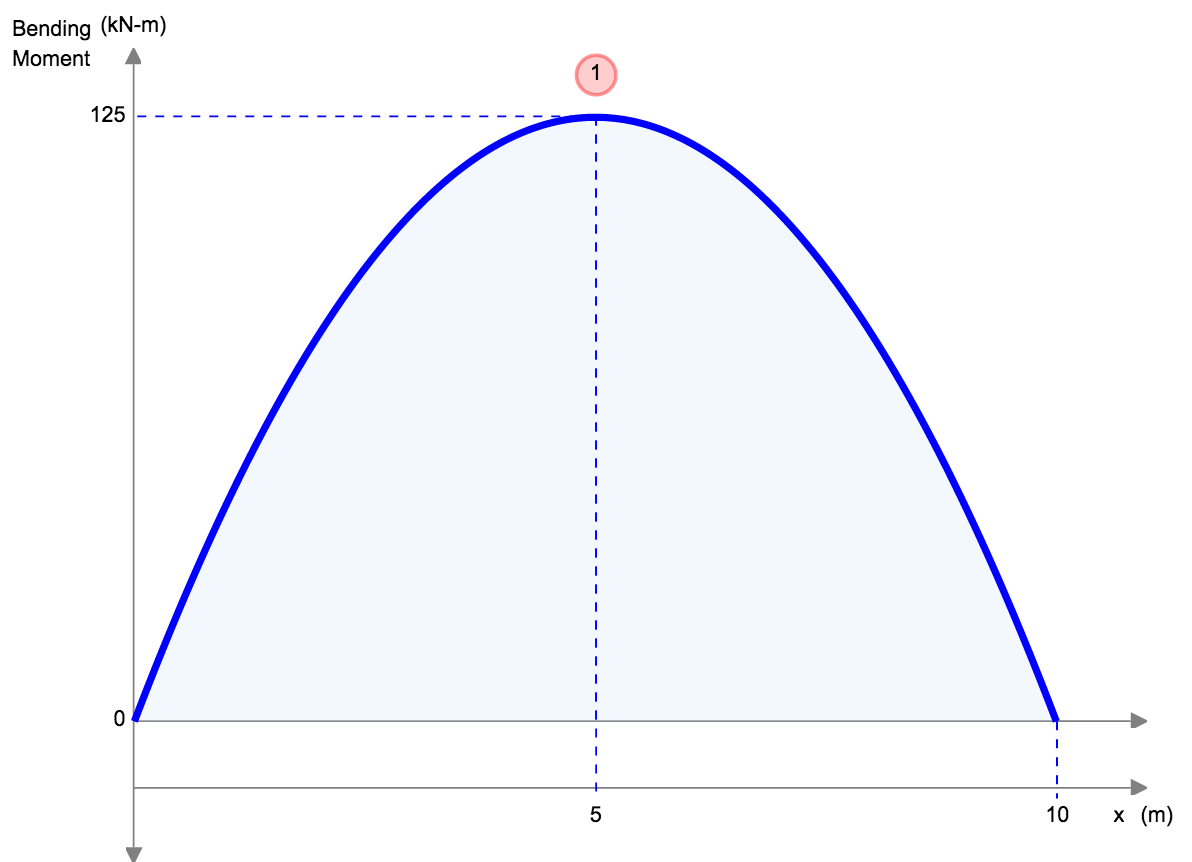
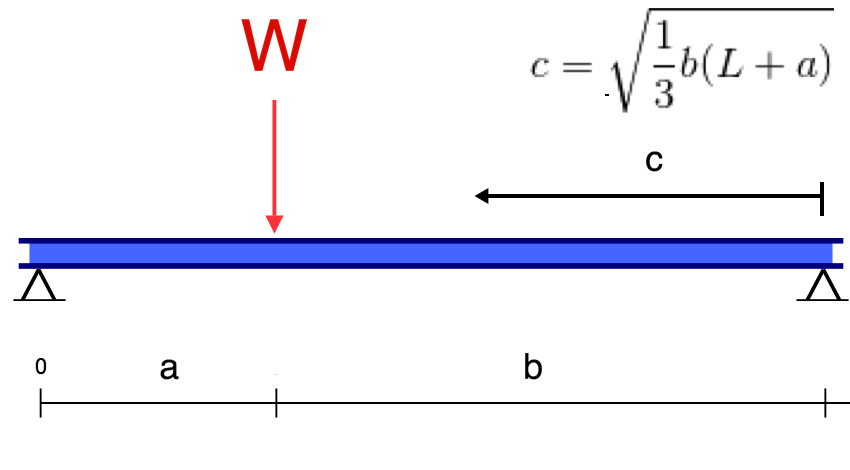
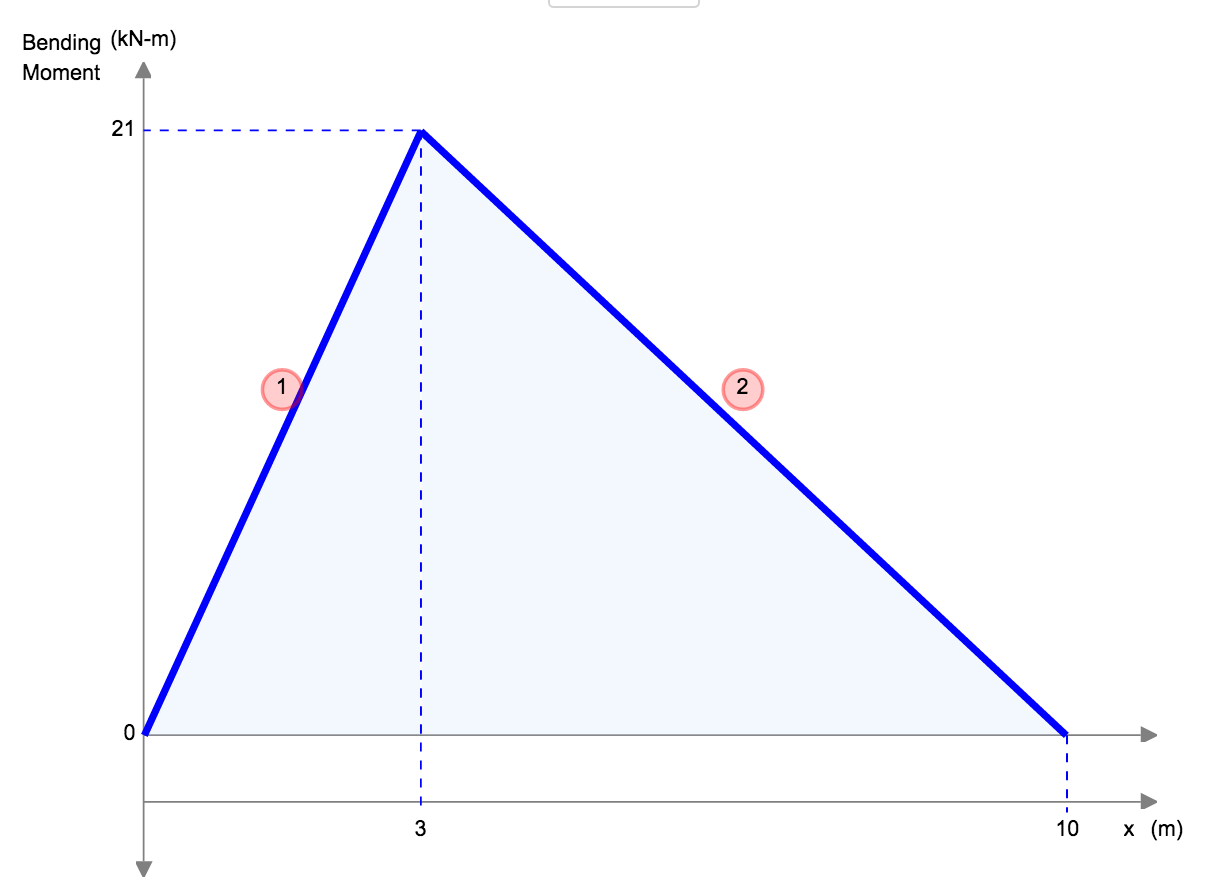
Een ander voorbeeld van doorbuiging is de doorbuiging van een eenvoudig ondersteunde balk. Deze balken worden aan beide uiteinden ondersteund, dus de doorbuiging van een balk is over het algemeen links en volgt een heel andere vorm dan die van de uitkraging. Onder een gelijkmatig verdeelde belasting (bijvoorbeeld het eigen gewicht), zal de balk soepel doorbuigen en naar het midden toe afbuigen.
| Referentie | Max doorbuiging | BMD-vorm |
 |
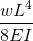 |
 |
 |
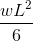 |
 |
 |
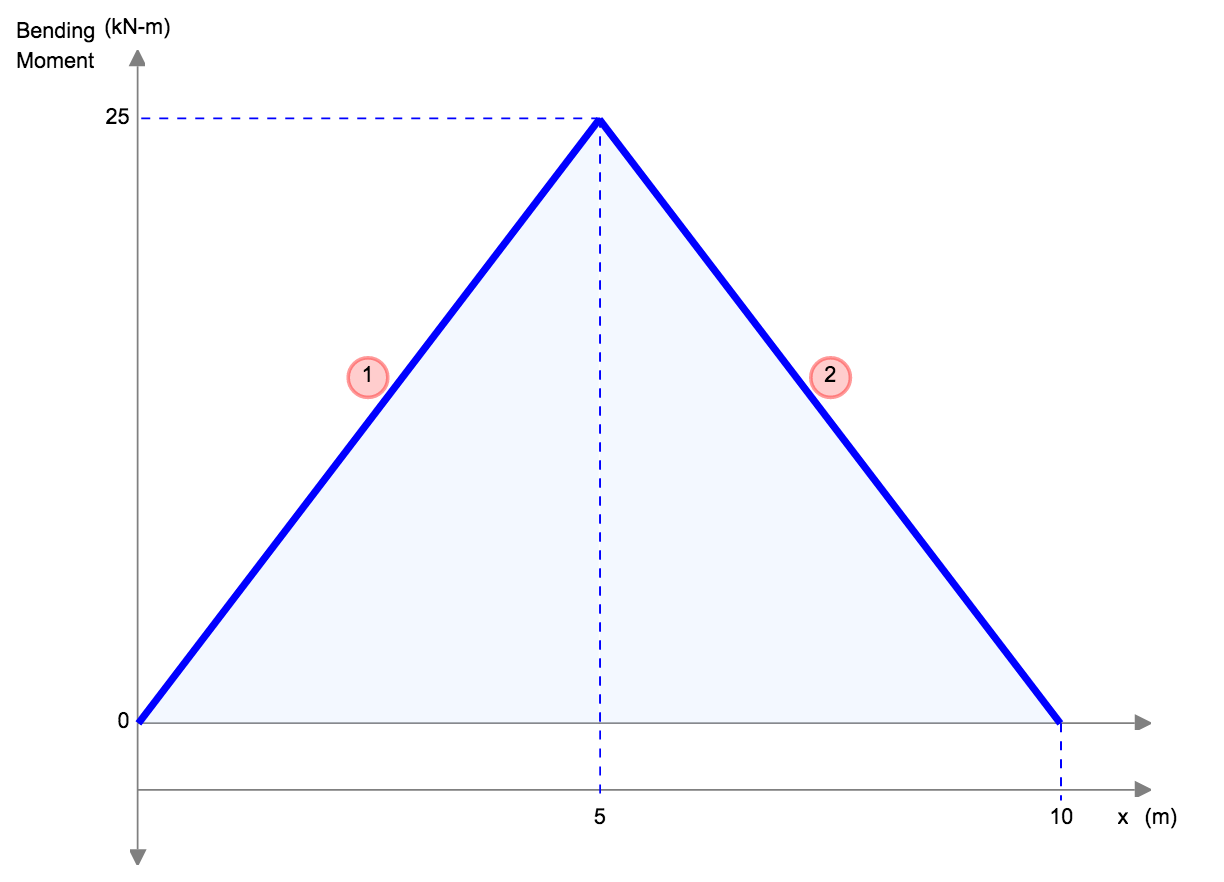
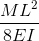 |
 |
 |
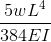 |
 |
 |
 |
 |
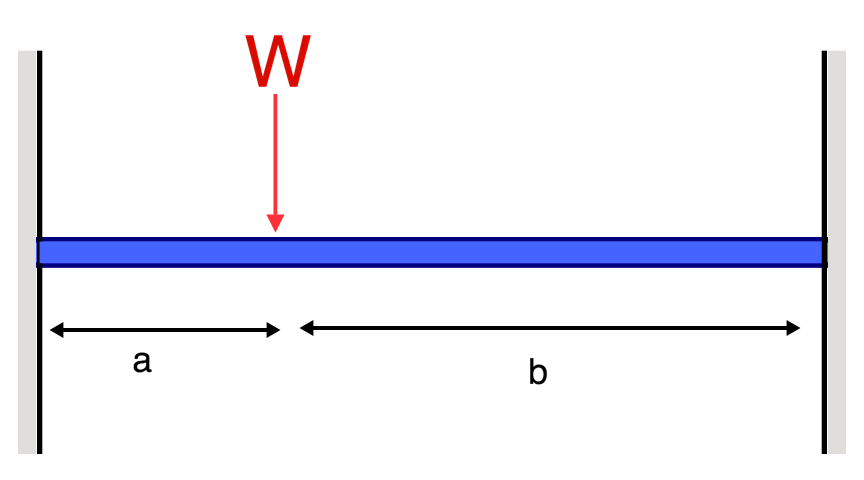
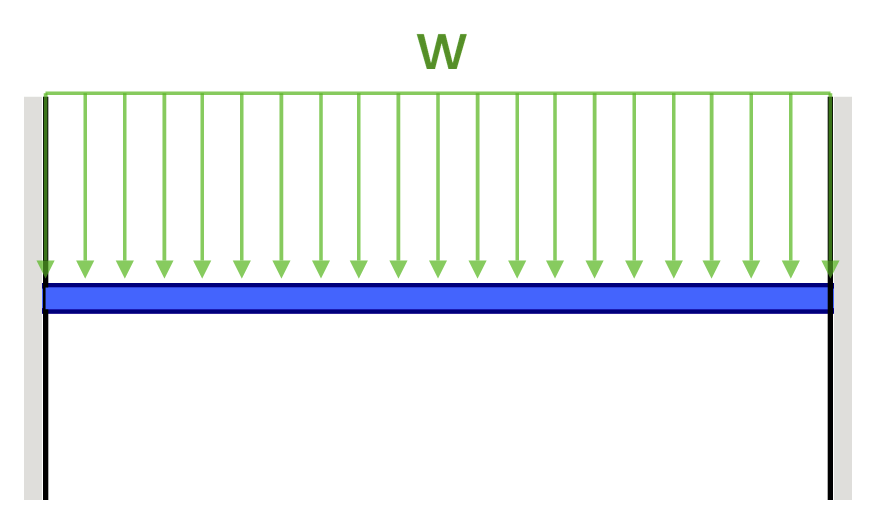
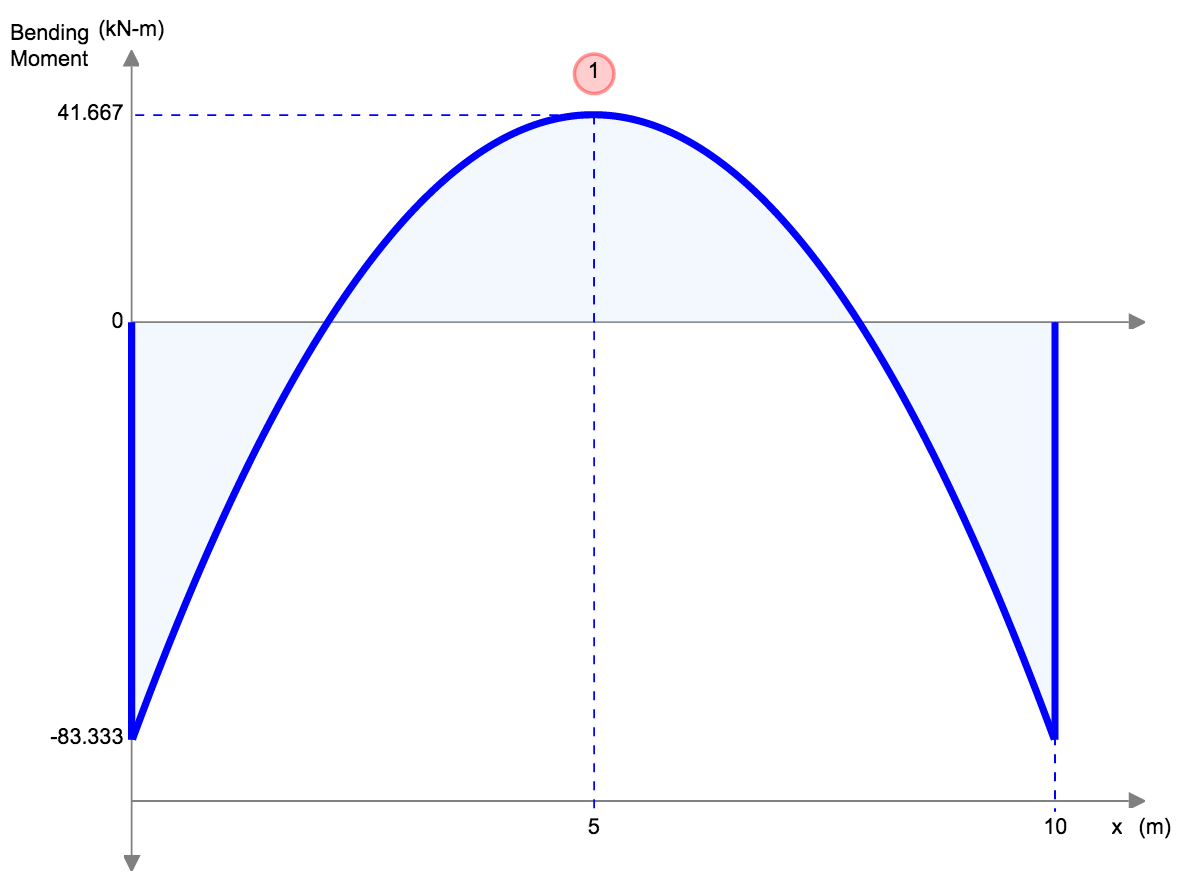
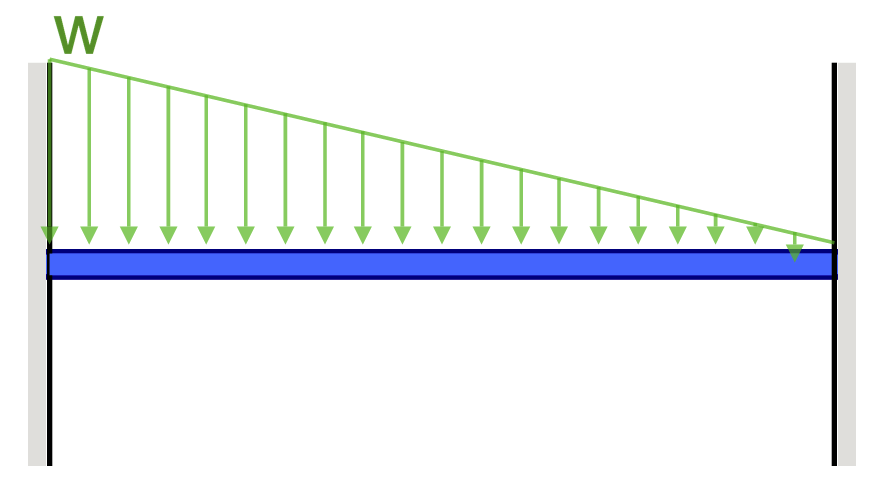
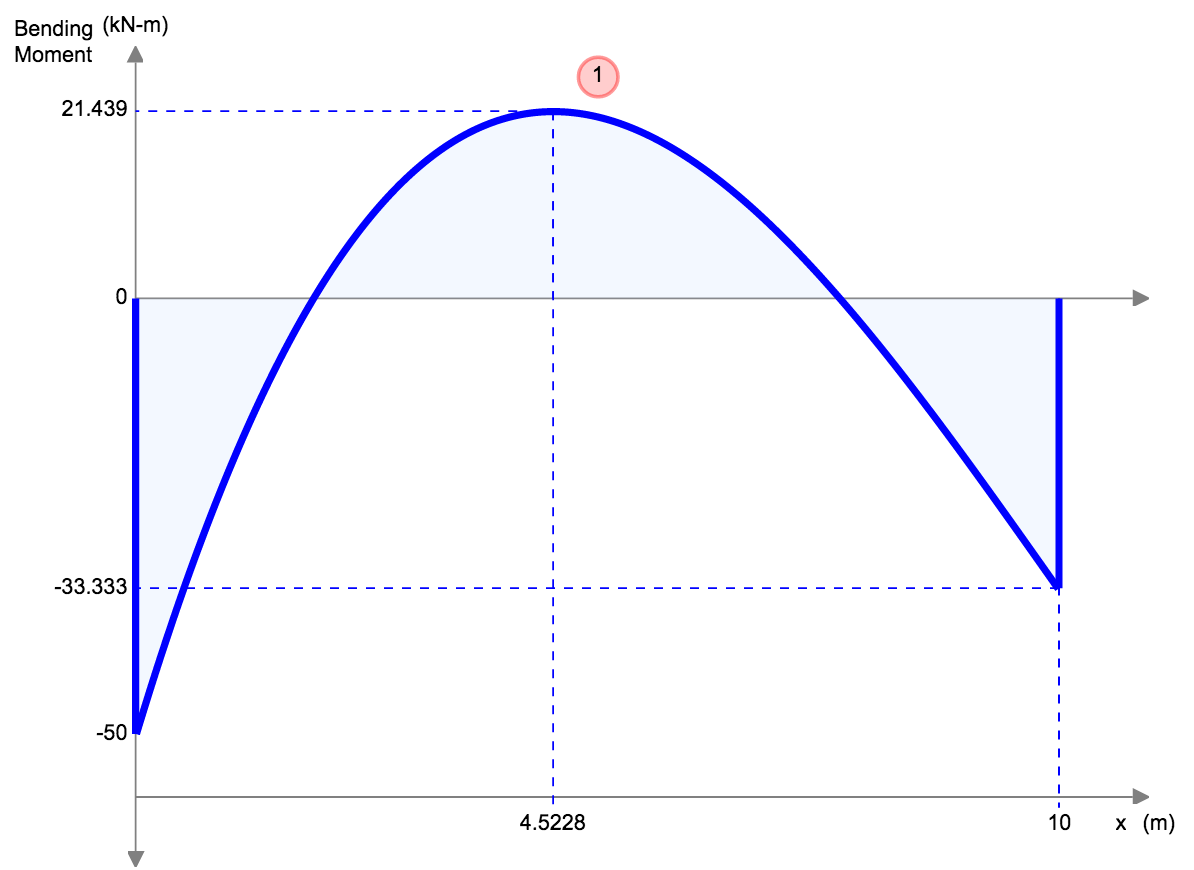
Doorbuigingsvergelijkingen/Formules voor Ingeklemde Balk
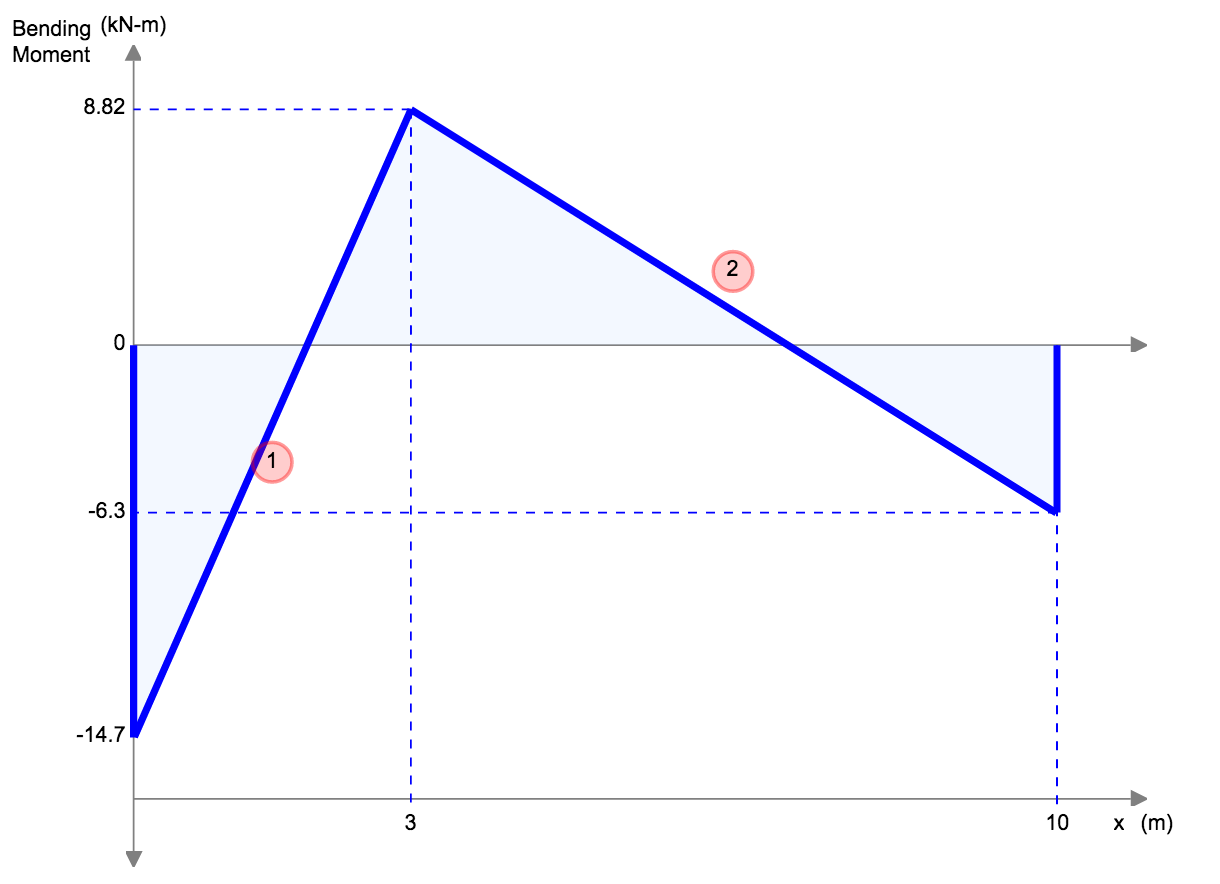
| Referentie | Max doorbuiging | BMD-vorm |
 |
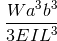 |
 |
 |
 |
 |
 |
 |
 |
4. Voorbeeld Berekening van Doorbuiging voor Eenvoudig Ondersteunde Balk
Laten we een eenvoudig ondersteunde balk overwegen met een overspanning van L = 10 m, een gelijkmatige belasting van w = 10,000 N / m, en de volgende materiaaleigenschappen: Young's modulus, E = 200 GPa, het traagheidsmoment, I = 0.0015 m^4.
De doorbuiging van de balk kan worden berekend met behulp van de vergelijking, genomen uit onze bovenstaande tabel met vergelijkingen:
\(d = (5w^4)/(384NEE) \)
\(d = (5 * 10,000 * 10^ 4)/(384 * 200 *10^9 * 0.0015) \)
\(d = 0.00434 meter = 4,34 mm \)
Dus de doorbuiging van de balk is 0.00434 m of 4.34 mm. Het is altijd belangrijk voor een ingenieur om je resultaat te verifiëren, dus laten we dezelfde nummers aansluiten op SkyCiv's Gratis Balk Calculator:
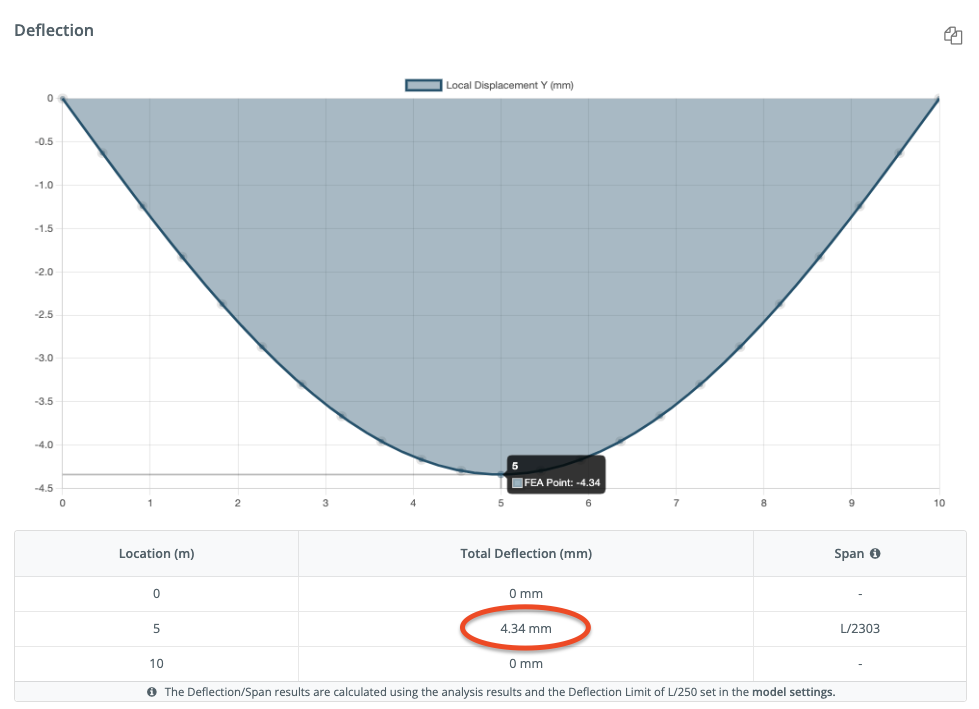
Het is de moeite waard om te vermelden dat dit een heel eenvoudig voorbeeld is en dat er in de praktijk, erschillende andere factoren in aanmerking moeten worden genomen zoals de effecten van temperatuurverandering, live load, eigen gewicht en vele andere zaken, in een reële situatie zou, een constructief ingenieur deze factoren in overweging nemen bij het berekenen van de doorbuiging van een balk.
SkyCiv Balk Software
SkyCiv Balk Analyse Software stelt gebruikers in staat om balkconstructies eenvoudig en nauwkeurig te analyseren. Je kunt binnen enkele seconden een analyse van je balkelement krijgen, inclusief reacties, dwarskracht, buigmoment, doorbuiging, en spanningen.
Als je het eerst wilt proberen, onze GRATIS Balk Doorbuiging Calculator een geweldige manier om te beginnen, of meld je vandaag nog gratis aan!

 Bron:
Bron: 
