Een volledig uitgewerkt voorbeeld van NBCC 2015 sneeuwbelasting berekeningen
Ophoping van sneeuw op constructies kan zeer gevaarlijk zijn voor dakelementen of andere blootgestelde structurele elementen. De Nationale bouwcode van Canada (2015) Divisie B – Sectie 4.1.6 geeft een gedetailleerde berekening van de sneeuwbelasting en de bijbehorende regenbelasting. Deze richtlijn gebruiken this, we zullen demonstreren hoe we de sneeuwbelasting kunnen berekenen met behulp van een voorbeeld Structurele 3D (S3D) magazijnmodel, zoals hieronder weergegeven:
Figuur 1: Voorbeeld S3D magazijnmodel

Figuur 2: Voorbeeld locatie locatie met Google Maps (alleen ter illustratie).
Tafel 1: Gebouwgegevens die nodig zijn voor onze sneeuwlastberekening.
| Plaats | Ogden, Calgary, Alberta (alleen ter illustratie) |
| Bezetting | Magazijn of opslag van materialen |
| Dimensies | 19.508 m x 31.70 m voor elke structuur Dakrandhoogte van kleiner gebouw 9.144 m Tophoogte van kleiner gebouw 11.941 m Het verschil tussen boven- en onderdak is: 3.50 m Dakhellingshoek 16° |
| aanvullende details | Dak heeft een glad oppervlak Kloof tussen structuren is 2.30 m |
Van tafel 1, de opgegeven sneeuwbelasting:, \(S), kan worden berekend met behulp van de formule:
\(S = {I}_{s}[{S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{een} +{S}_{r}]\) (1)
Waarbij:
\({I}_{s}\) = belangrijkheidsfactor voor sneeuwbelasting, Tabel 4.1.6.2-A
\({S}_{s}\) = 1-in-50 jaar sneeuwbelasting op de grond, kPa, onderafdeling 1.1.3
\({C}_{b}\) = basis sneeuwbelastingsfactor voor daken, 4.1.6.2 (2)
\({C}_{w}\) = windblootstellingsfactor gebaseerd, 4.1.6.2 (3) en (4)
\({C}_{s}\) = hellingsfactor, 4.1.6.2 (5), (6), en (7)
\({C}_{een}\) = accumulatiefactor, 4.1.6.2 (8)
\({S}_{r}\) = 1-in-50 jaar gerelateerde regenbelasting, kPa, onderafdeling 1.1.3, maar niet groter dan \({S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{een}\)
Elke parameter zal afzonderlijk worden onderzocht in de volgende secties:. De volgende gevallen van sneeuwbelasting worden berekend:: uitgebalanceerde en ongebalanceerde sneeuwbelasting op elk dak (wind normaal tot kam), evenals de drift die op het onderste dak wordt gegenereerd, rekening houdend met accumulatie door glijden.
Belang Factor:, \({I}_{s}\)
Het eerste dat wordt bepaald, is de belangrijkheidsfactor, \({I}_{s}\), die wordt gevonden met behulp van Tabel 4.1.6.2-A zoals waarnaar wordt verwezen. Aangezien de structuur een opslaggebouw is dat bij storing een lage directe impact heeft op het menselijk leven, de belangrijkheidscategorie is Laag. Bovendien, de berekening bevindt zich in de uiterste grenstoestand (ULS). dus van Tabel 4.1.6.2-A, \({I}_{s}\) is gelijk aan 0.80.
| Belang categorie | Belang Factor:, \({I}_{s}\) | |
|---|---|---|
| ULS | SLS | |
| Laag | 0.8 | 0.9 |
| Normaal | 1.0 | 0.9 |
| hoog | 1.15 | 0.9 |
| Post-ramp | 1.25 | 0.9 |
Sneeuwbelasting op de grond, \({S}_{s}\), en bijbehorende regenbelasting, \(({S}_{r})\)
De sneeuwbelasting op de grond, \({S}_{s}\), en bijbehorende regenbelasting, \(({S}_{r})\), waarden worden getabelleerd in Bijlage C, Divisie B van NBCC 2015 afhankelijk van locatie en provincie. Voor dit voorbeeld, de overeenkomstige \({S}_{s}\) en \(({S}_{r})\) in Calgary, Alberta is gelijk aan 1.10 kPa en 0.1 kPa, respectievelijk.
Moeite hebben met het zoeken naar de grondsneeuw en de bijbehorende regenbelasting voor NBCC 2015? Proberen de SkyCiv Free Load Generator Tool om uw zoekopdracht te versnellen en de bijbehorende te krijgen \({S}_{s}\) en \({S}_{r}\) op basis van de locatie van uw structuur.
Windblootstellingsfactor, \({C}_{w}\)
Voor de windblootstellingsfactor, \({C}_{w}\), het is toegestaan gelijk te zijn aan 1.0 te krijgen op basis van 4.1.6.2 (3). Deze factor kan nog worden verlaagd zolang de omstandigheden 4.1.6.2 (4) is tevreden. Voor dit voorbeeld, \({C}_{w}\) zal gelijk zijn aan 1.0 aangezien de locatie geen open terrein is dat de structuur volledig aan de wind blootstelt.
Basis sneeuwbelastingsfactor voor daken, \({C}_{b}\)
De basissneeuwbelastingsfactor op het dak:, \({C}_{b}\), kan worden berekend met behulp van de volgende formules:, zoals vermeld in 4.1.6.2 (2):
\({C}_{b} = 0.8\) (2) voor \({l}_{c} ≤ (70/{{C}_{w}}^{2})\) en
\({C}_{b} = (1/{C}_{w}) [1 – (1 – 0.8{C}_{w})exp(-0.01({l}_{c}{{C}_{w}}^{2} – 70))] \) (3) voor \({l}_{c} > (70/{{C}_{w}}^{2})\)
Waarbij:
\({l}_{c}\) = karakteristieke lengte van het bovenste of onderste dak gedefinieerd als: \(2w -{w}^{2}/l\)
\(l\) = grotere bovenafmeting van het dak
\(w\) = kleinere bovenafmeting van het dak
Voor dit voorbeeld,\(l\) en \(w\) is gelijk aan 31.7 m en 19.51 m, respectievelijk, Vandaar, \({l}_{c}\) is gelijk aan 27.01. Sinds \({l}_{c}\) is minder dan \((70/{1.0}^{2})\), de basissneeuwbelasting op het dak, \({C}_{b}\), is gelijk aan 0.8.
Hellingsfactor, \({C}_{s}\)
De berekening van de hellingsfactor is \({C}_{s}\) gedetailleerd in 4.1.6.2 (5), (6), en (7) wordt hieronder weergegeven:.
Voor onbelemmerd glad dak:
\({C}_{s} = 1.0\) voor \(α ≤ 15°\)
\({C}_{s} = 0\) voor \(een > 60°\)
\({C}_{s} = (60° – een)/45°\) voor \(15° < α ≤ 60°\)
Voor andere gevallen::
\({C}_{s} = 1.0\) voor \(α ≤ 30°\)
\({C}_{s} = 0\) voor \(een > 70°\)
\({C}_{s} = (70° – een)/40°\) voor \(30° < α ≤ 70°\)
Specifiek gewicht van sneeuw, \(γ\)
Het soortelijk gewicht van sneeuw wordt gespecificeerd in: 4.1.6.13 en zal worden genomen als:
\(= 0.43{S}_{s} + 2.2 kN/{m}^{3} ≤ 4.0kN/{m}^{3}\) (4)
Voor dit voorbeeld, \(γ\) is gelijk aan \(2.673 kN/{m}^{3}\).
Accumulatiefactor, \({C}_{een}\)
Accumulatiefactor, \({C}_{een}\), ik ik 4.1.6.2 (8). ik.
Opgegeven sneeuwbelasting, \(S)
In deze sectie, de gespecificeerde sneeuwbelasting, \(S), zal worden berekend voor de gebalanceerde en afgedreven gevallen.
Evenwichtige/ongestuurde behuizing
Voor de gebalanceerde/ongestuurde behuizing, de accumulatiefactor \({C}_{een}\) is gelijk aan 1.0. Bovendien, ik \(α\) is \(16°\) en het dakoppervlak wordt verondersteld onbelemmerd glad te zijn, de hellingsfactor, \({C}_{s}\), voor ons voorbeeld is gelijk aan 0.978. Met behulp van vergelijking (1), de opgegeven sneeuwbelasting:, \(S), voor gebalanceerde/ongestuurde koffer is:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa
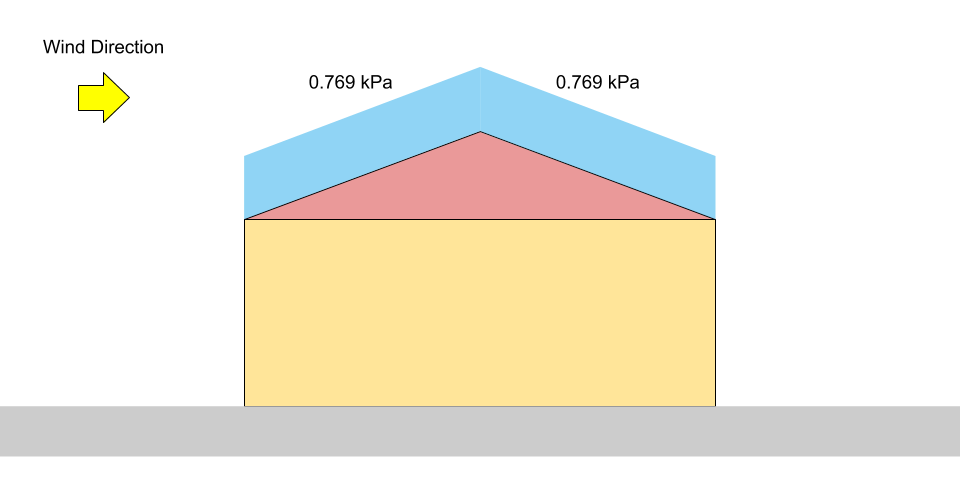
Figuur 3: Belastingsdiagram voor evenwichtige sneeuwbelasting op een zadeldak.
Ongebalanceerde/afgedreven behuizing
Wind die normaal tot richel werkt
Omdat de constructies zadeldaken hebben, de onevenwichtige sneeuwbelasting (wind die normaal op de nok staat) accumulatiefactor \({C}_{een}\) wordt gevonden met behulp van 4.1.6.9:
\({C}_{een, tegen de wind in} = 0\)
\({C}_{een, benedenwinds} = 0.25 +α/20\) voor \(15° ≤ α ≤ 20°\)
\({C}_{een, benedenwinds} = 1.25\) voor \(20° < α ≤ 90°\)
Omdat beide constructies een dakhellingshoek hebben die gelijk is aan 16°, de accumulatiefactoren \({C}_{een, tegen de wind in}\) en \({C}_{een, benedenwinds}\) zijn gelijk aan 0 en 1.05, respectievelijk. Bovendien, ik \(α\) is \(16°\) en het dakoppervlak wordt verondersteld onbelemmerd glad te zijn, de hellingsfactor, \({C}_{s}\), voor ons voorbeeld is gelijk aan 0.978.
In het ongebalanceerde/afgedreven geval loodrecht op de nok, \({C}_{een}\) wordt berekend op basis van 4.1.6.9 voor een zadeldakgeval. Uit de bovenstaande berekening, \({C}_{een, tegen de wind in} = 0\) en \({C}_{een, benedenwinds} = 1.05\). Vandaar, de opgegeven sneeuwbelastingen voor elke zijde zijn::
\({S}_{tegen de wind in} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({p}_{1}\)
\({S}_{benedenwinds} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({p}_{2}\)
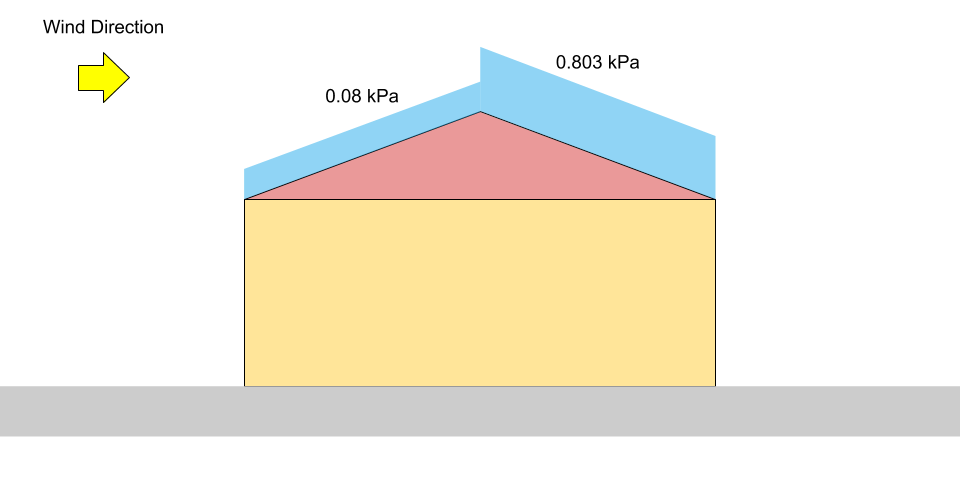
Figuur 4: Belastingsdiagram voor ongebalanceerde sneeuwbelasting op een zadeldak (niet op schaal).
Wind parallel aan de kam – Geval I – Wind van boven naar beneden dak
Wanneer de wind evenwijdig aan de nok werkt, er zal hoogstwaarschijnlijk een sneeuwbank ontstaan op het onderste dak. ik accumulatiefactor \({C}_{een}\), de volgende formules van 4.1.6.2 (8) worden gebruikt:
\({C}_{een} ={C}_{a0} – ({C}_{a0} – 1)(X/{X}_{d})\) voor \(0 ≤ x ≤ {X}_{d}\)
\({C}_{een} = 1.0\) voor \(X > {X}_{d}\)
Waarbij:
\({C}_{a0}\) = piekwaarde van \({C}_{a0}\) bij x = 0
\(x\) = afstand vanaf dakstap
\({X}_{d}\) = lengte van de drift zoals weergegeven in figuur 3 hieronder

Figuur 5: Illustratie van dakafmetingsparameters

Figuur 6: Overeenkomstige driftbelasting op het onderste dak op basis van: Afbeelding 4.1.6.5-A.
\({C}_{a0}\) en \({X}_{d}\) kan worden berekend met behulp van de volgende formules::
\({C}_{a0} = frac{h}{{C}_{b}{S}_{s}}\) of \({C}_{a0} = frac{F}{{C}_{b}}\) (5), wat minder is
\({X}_{d} = 5 \frac{{C}_{b}{S}_{s}}{c}({C}_{a0} – 1)\) (6)
\(F = 0.35β\sqrt{\frac{c({l}_{cs} – 5{{h}_{p}}^{‘})}{{S}_{s}}} +{C}_{b}\) maar \(F ≤ 5\) voor \({C}_{ws} = 1.0\) (7)
\({h}^{‘} = h – \frac{{C}_{b}{C}_{w}{S}_{s}}{c}\) (8)
\({{h}_{p}}^{‘} ={h}_{p} – \frac{0.8{S}_{s}}{c}\) maar \(0 ≤ {{h}_{p}}^{‘} ≤ \frac{{l}_{cs}}{5}\) (9)
Waarbij:
\({h}_{p}\) = hoogte borstwering op bovendak (0 in dit geval omdat er geen borstwering is)
\(h ) = hoogteverschil tussen bovenste en onderste dakniveau
\({C}_{ws}\) = waarde van \({C}_{w}\) van toepassing op de bron van drift
\({l}_{cs}\) = karakteristieke lengte van het brongebied gedefinieerd als: \(2{w}_{s} -{{w}_{s}}^{2}/{l}_{s}\)
\({l}_{s}\) = grotere plandimensie van het brongebied zoals weergegeven in figuur 7 en 8, hieronder weergegeven
\({w}_{s}\) = kleinere plandimensie van het brongebied zoals weergegeven in figuur 7 en 8, hieronder weergegeven
\(β\) = 1.0 voor geval I, en 0.67 voor Case II en III.
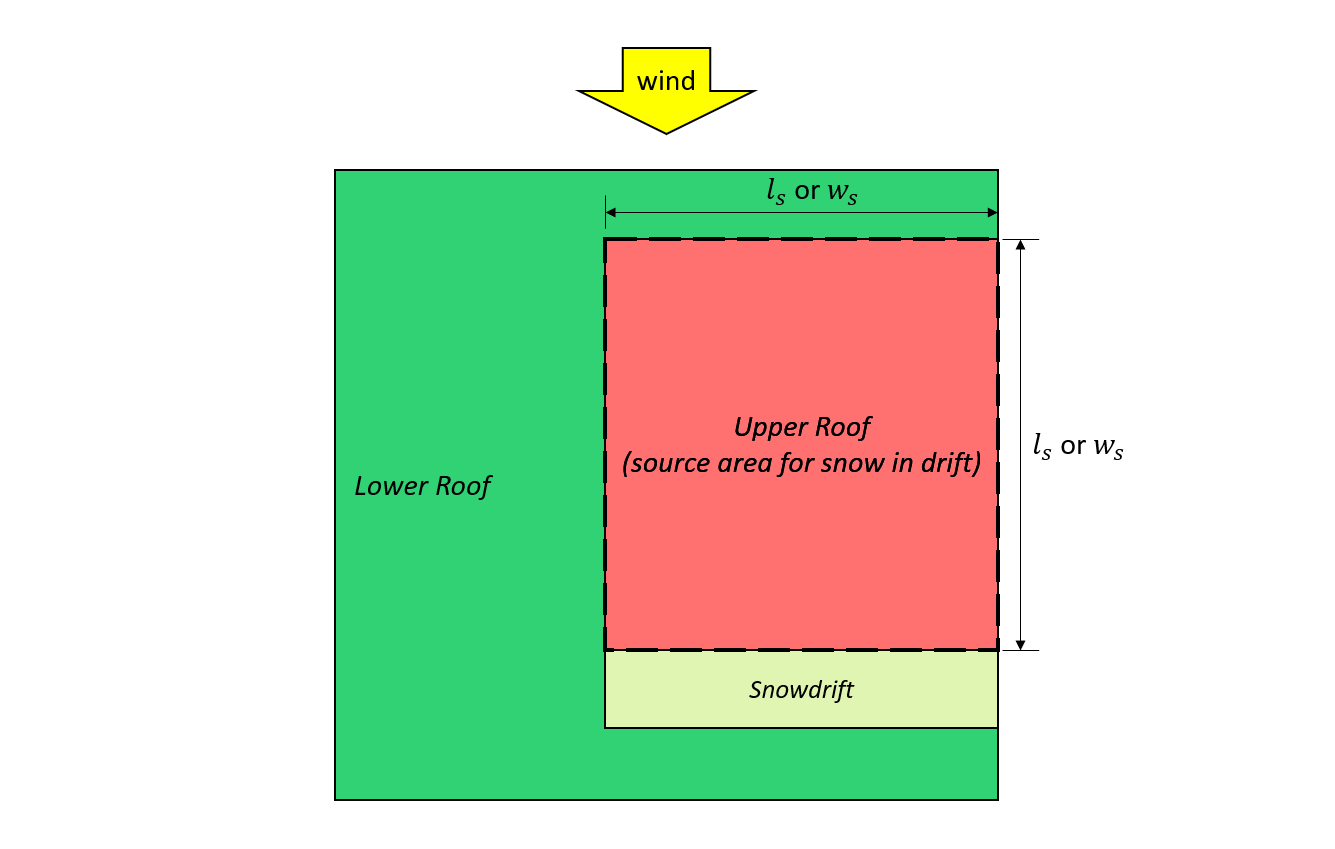
Figuur 7: Geval I – sneeuwbank gevormd door de wind afkomstig van het bovenste dak op basis van Afbeelding 4.1.6.5-B.
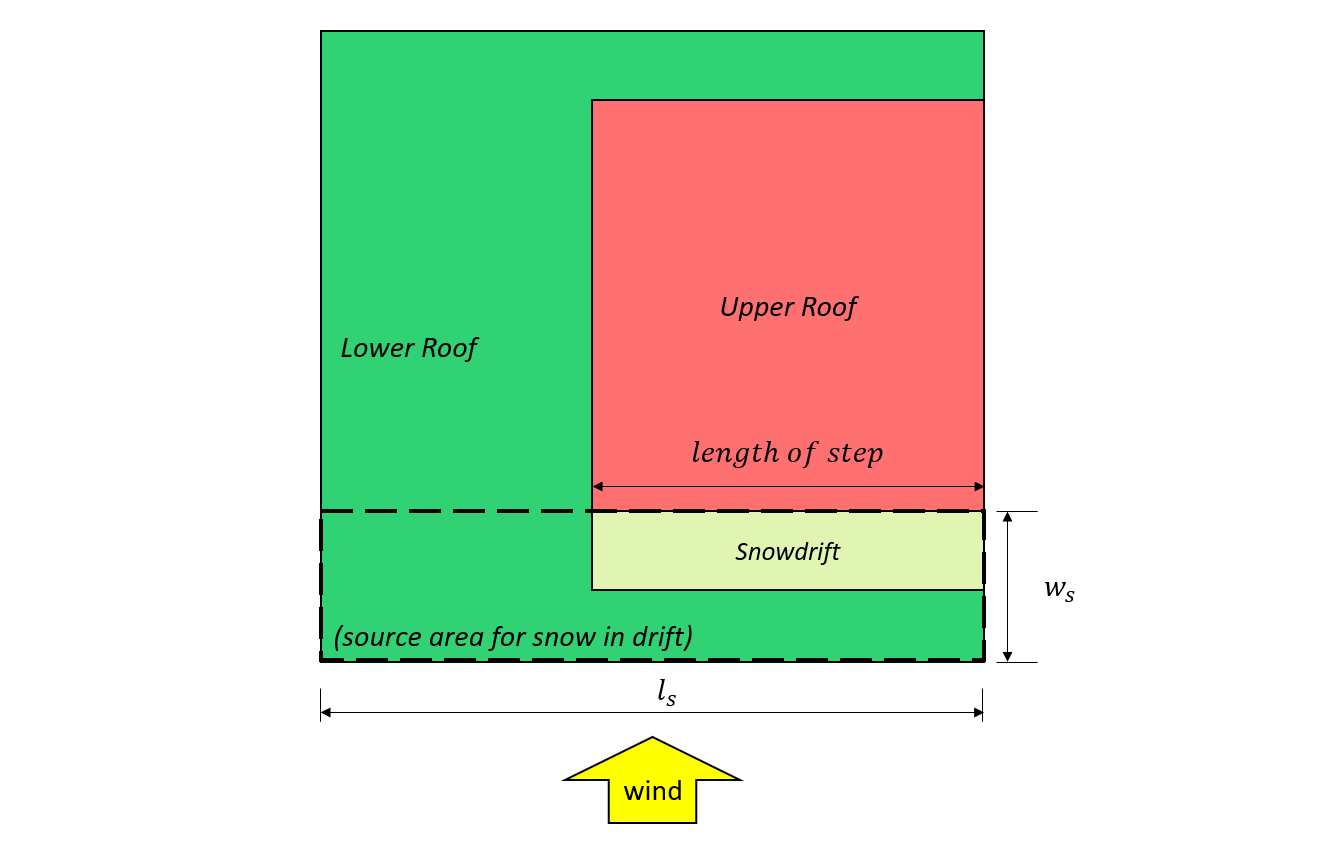
Figuur 8: Geval II – sneeuwbank gevormd door de wind afkomstig van het onderste dak op basis van: Afbeelding 4.1.6.5-B.
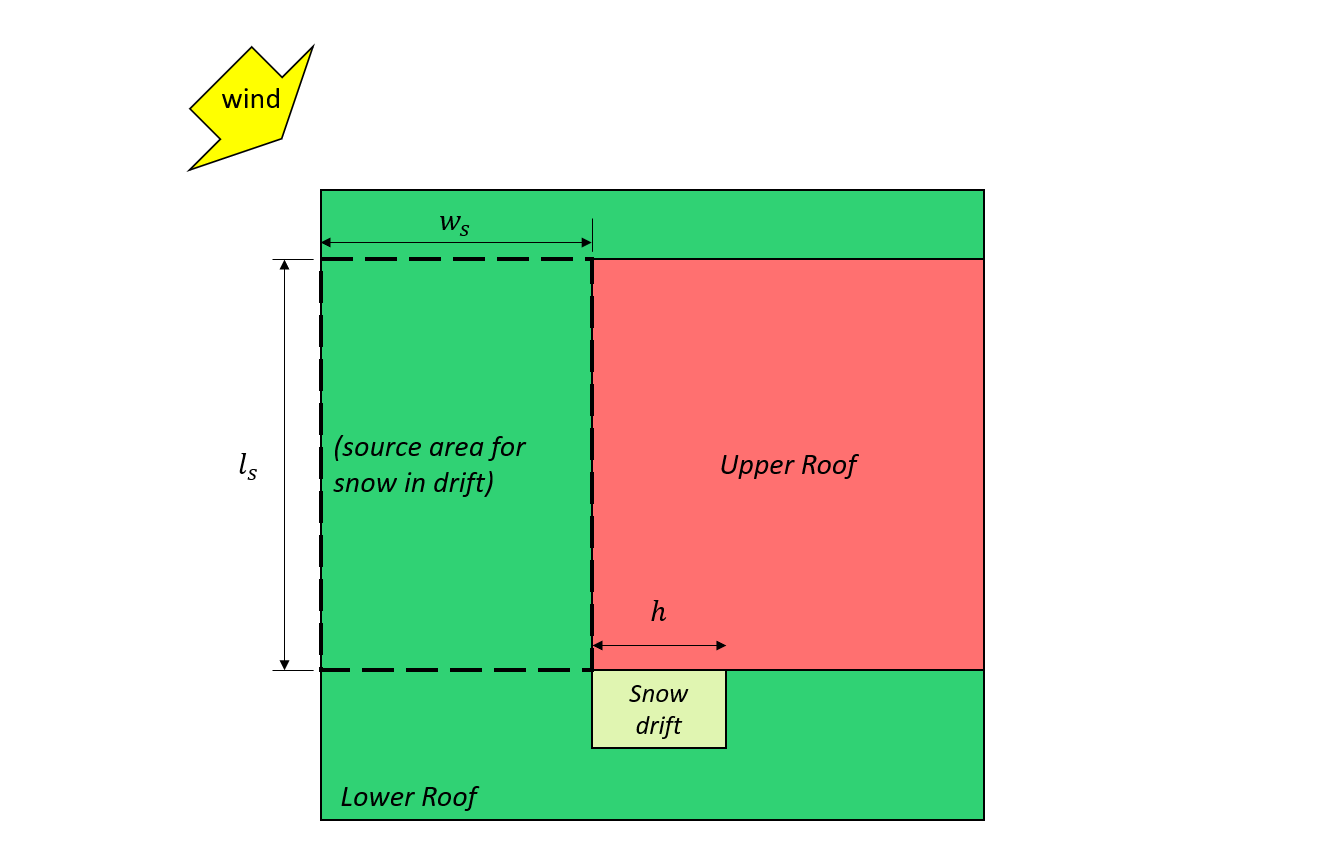
Figuur 7: Geval III – gedeeltelijke sneeuwbank gevormd door de wind afkomstig van het onderste dak op basis van: Afbeelding 4.1.6.5-B.
Voor dit voorbeeld, Gevallen I en II zullen worden overwogen.
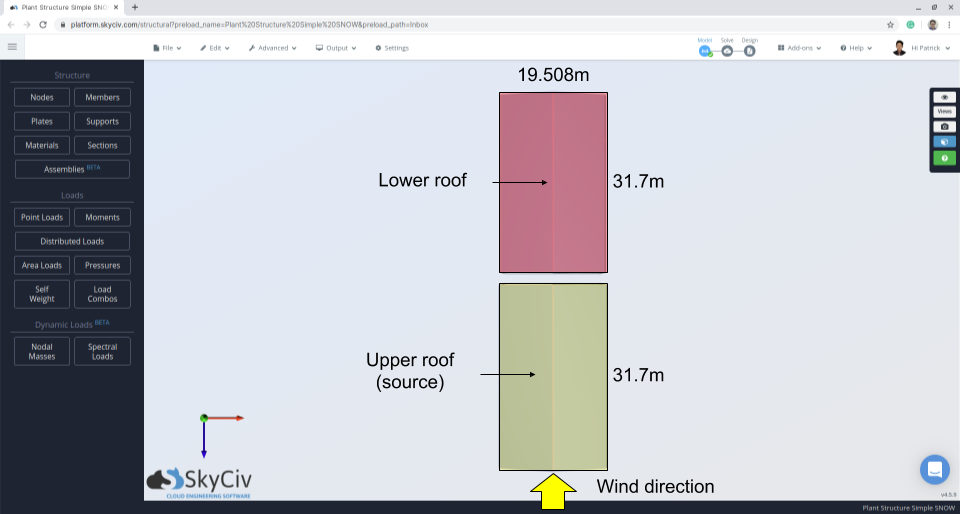
Figuur 10: Structuurplan met aanduiding van windrichting en brongebied.
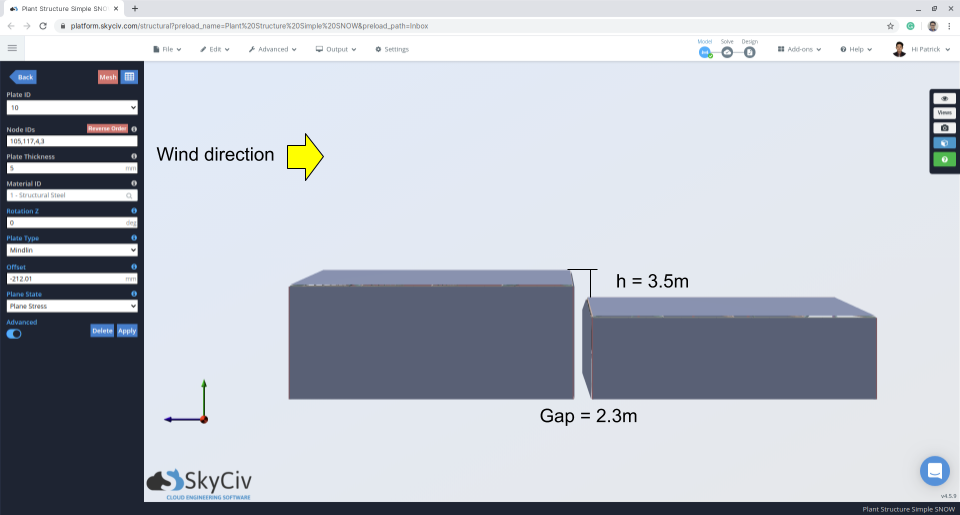
Figuur 11: Hoogteweergave die de opening en het verschil tussen het bovenste en onderste dak aangeeft.
Voor de ongebalanceerde/afgedreven behuizing evenwijdig aan de nok, \({C}_{een}\) wordt berekend voor Case I en Case II op basis van: 4.1.6.5 voor het dak met meerdere niveaus. Voor geval I, deze volgende parameters moeten eerst worden berekend met behulp van de verschillende vergelijkingen die eerder in dit voorbeeld zijn genoemd::
\(= 1.0\)
\({h}^{‘} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 [object Window])
\({h}_{p} = 0\)
\({{h}_{p}}^{‘} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 [object Window])
\(F = 0.35(1.0)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) of \({C}_{a0} = frac{3.66}{0.8} = 4.544\)
\({C}_{a0} = 4.544\)
\({X}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 [object Window])
Van deze parameters, de accumulatiefactor, \({C}_{een}\), kan worden berekend door de waarde van te vervangen \({C}_{a0}\) bij elk \(x\) afstand. Houd er rekening mee dat we moeten berekenen \({C}_{een}\) Bij \(x = a\) waar \(een) is de afstand tussen het dak, aangezien de dakspleet kleiner is dan 5 m zoals gespecificeerd in 4.1.6.6.
Bij \(x = 0\): \({C}_{een} =4,544 – (4.544 – 1)(0/5.835) = 4.544\)
Bij \(x = a\): \({C}_{een} =4,544 – (4.544 – 1)(2.3/5.835) = 3.147\)
Bij \(x = {X}_{d}\): \({C}_{een} =1.0\)
Bij \(x = 10{h}^{‘}\): \({C}_{een} =1.0\)
ik ik ik, \({C}_{s} = 1.0\). Bovendien, bij het vinden van de gespecificeerde sneeuwbelasting op het bovenste dak, de accumulatiefactor, \({C}_{een}\), en hellingsfactor, \({C}_{s}\), zijn beide gelijk aan 1.0. Vandaar, de grootte van de gespecificeerde sneeuwbelastingen op elke locatie zijn:
Bij \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa\)
Bij \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
Bij \(x = {X}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
op bovenste dakniveau: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)
Wind parallel aan de kam – Geval II – Wind van onder naar boven dak
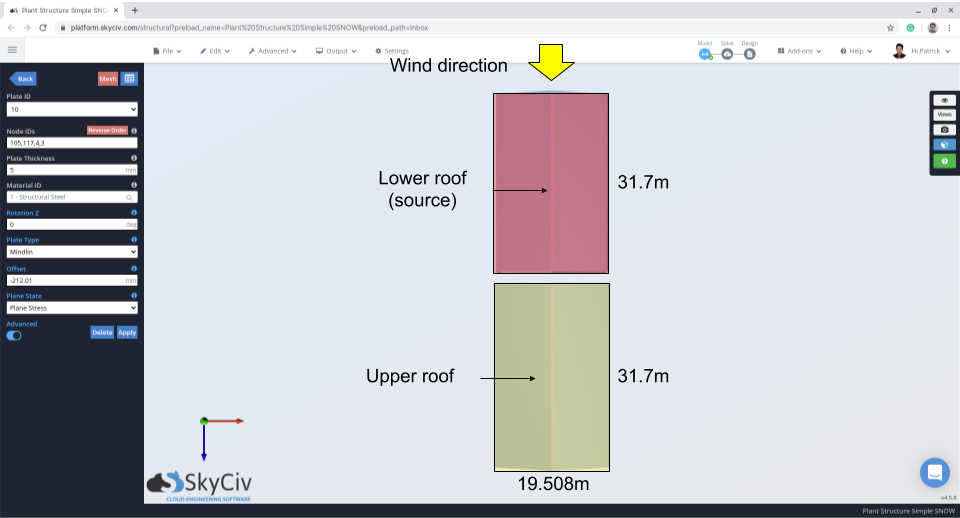
Figuur 12: Structuurplan met aanduiding van windrichting en brongebied – wind van onderdak naar boven.
Voor geval II, de berekening is vergelijkbaar met Case I, maar heeft een andere \(= 0.67\):
\(= 0.67\)
\({h}^{‘} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 [object Window])
\({h}_{p} = 0\)
\({{h}_{p}}^{‘} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 [object Window])
\(F = 0.35(0.67)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) of \({C}_{a0} = frac{2.70}{0.8} = 3.375\)
\({C}_{a0} = 3.375\)
\({X}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 [object Window])
Bij \(x = 0\): \({C}_{een} =3.375 – (3.375 – 1)(0/3.909) = 3.375\)
Bij \(x = a\): \({C}_{een} =3.375 – (3.375 – 1)(2.3/3.909) = 1.978\)
Bij \(x = {X}_{d}\): \({C}_{een} =1.0\)
Bij \(x = 10{h}^{‘}\): \({C}_{een} =1.0\)
Bij \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa\)
Bij \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
Bij \(x = {X}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
op bovenste dakniveau: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)
Ter illustratie:, de overeenkomstige \({p}_{1}\), \({p}_{2}\), en \({p}_{3}\) worden getoond in Figuren 13 en 14 hieronder voor zowel Case I als II, respectievelijk.
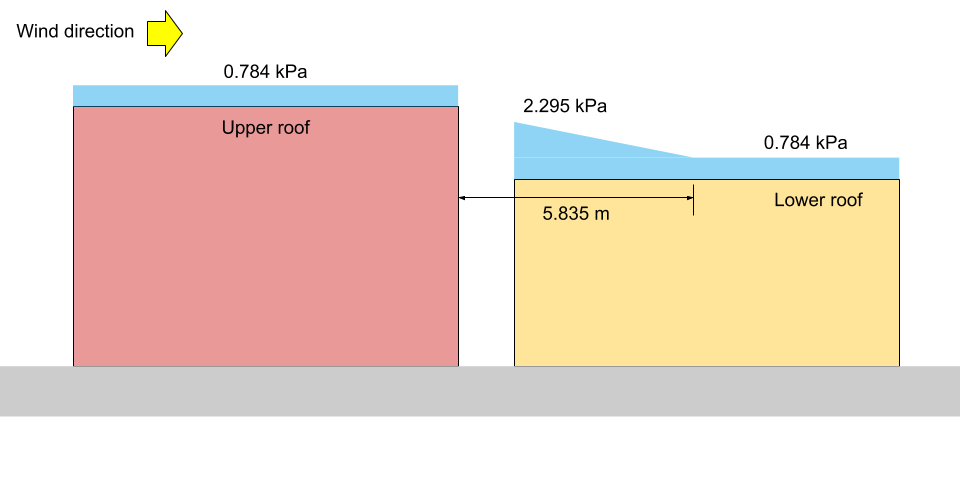
Figuur 13: Illustratie sneeuwbelasting voor Case I (niet op schaal).
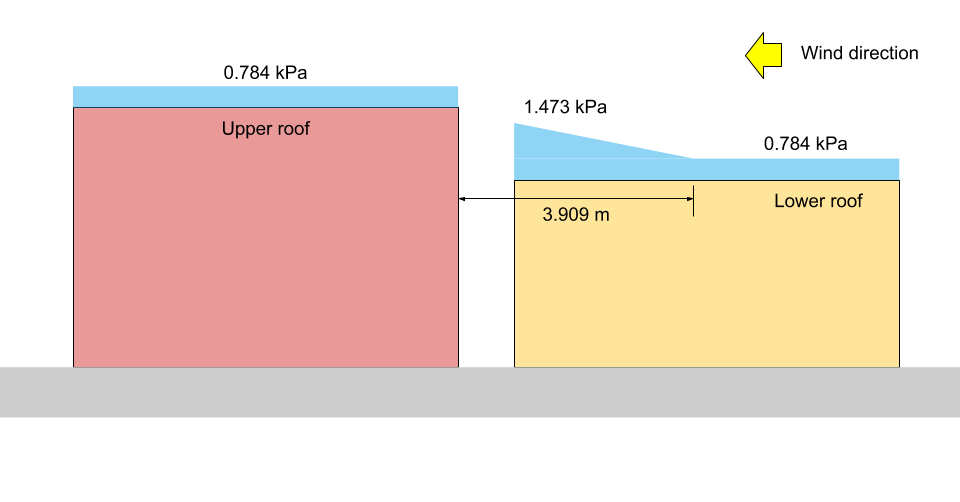
Figuur 14: Illustratie sneeuwbelasting voor Case II (niet op schaal).
Voltooi deze berekeningen automatisch in minuten
Dat was een lange rekensom, wat kun je als ingenieur doen om dit proces te versnellen voor je toekomstige projecten?? Onlangs heeft SkyCiv Snow Load Generator uitgebracht en geautomatiseerd als onderdeel van de SkyCiv Load Generator, die ook windbelastingen kan genereren. Om de sneeuwbelasting van het getoonde voorbeeld te vinden, het kost slechts een paar klikken om de tool te gebruiken:
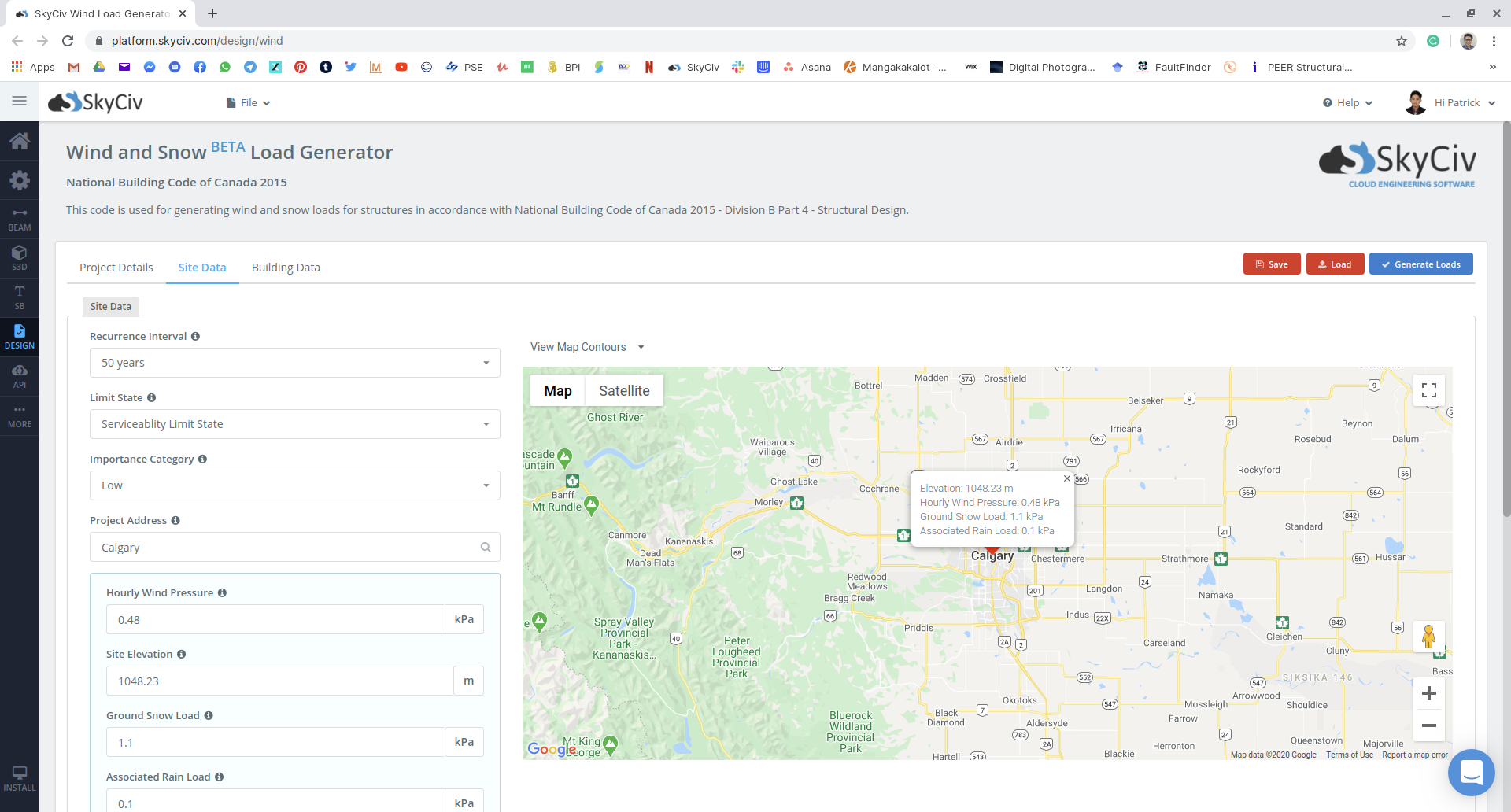
Figuur 15: Sitegegevensinvoer op SkyCiv Load Generator-module met behulp van ons voorbeeld.
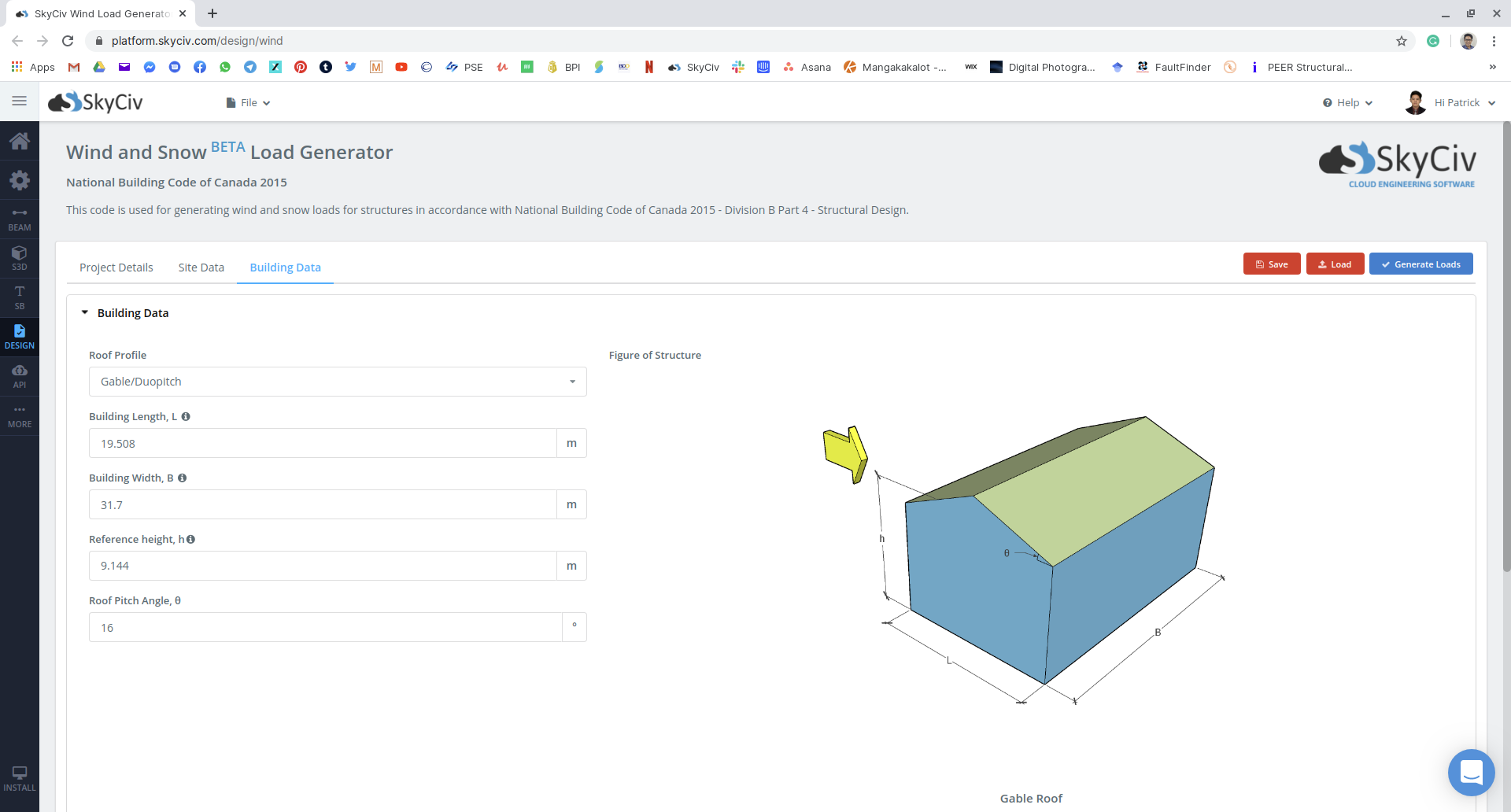
Figuur 16: Gebouw- en sneeuwparameterinvoer op SkyCiv Load Generator-module met behulp van ons voorbeeld.
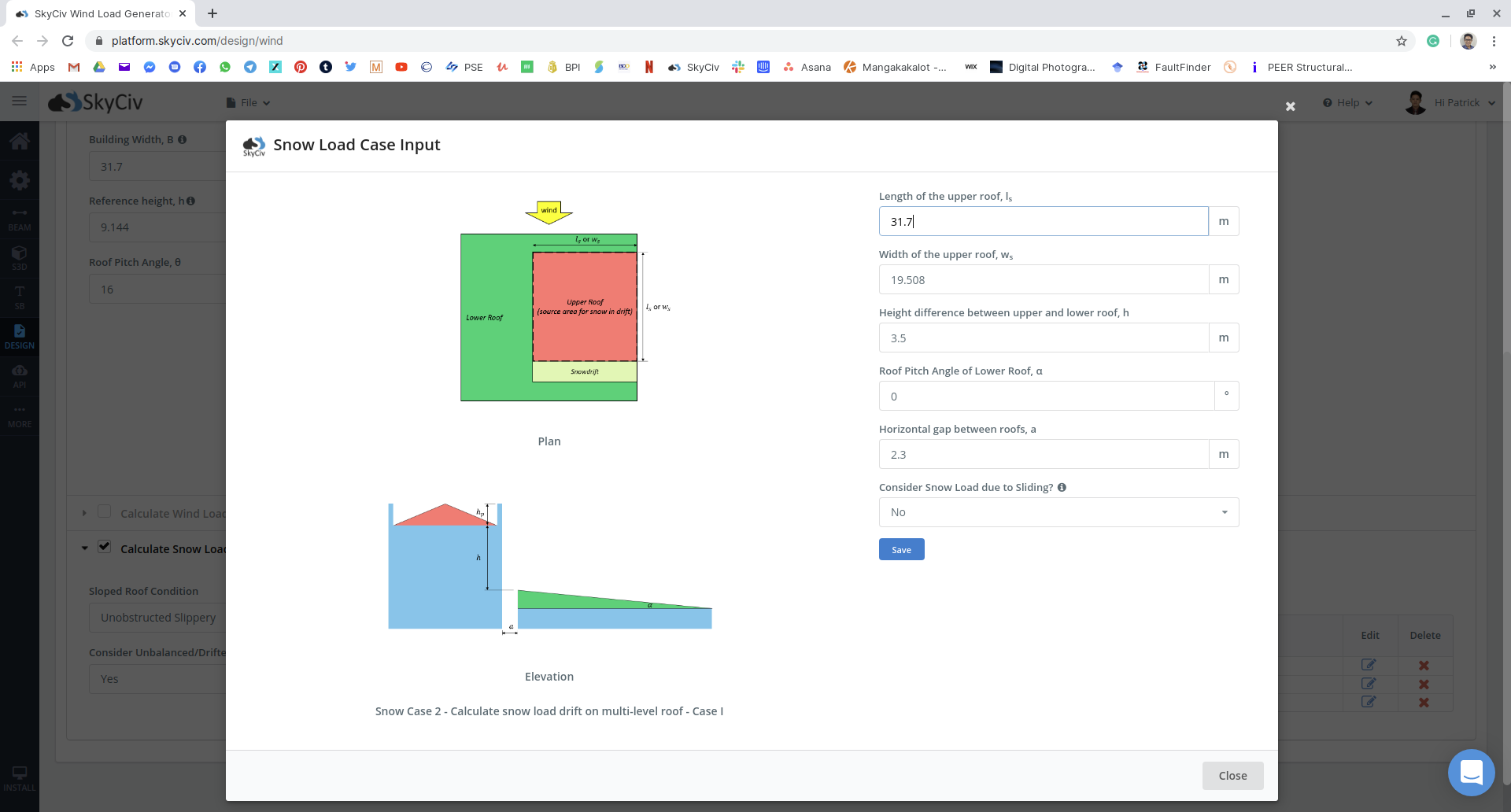
Figuur 17: Sneeuwbelastinginvoer voor meerdere ongebalanceerde gevallen voor het voorbeeld.
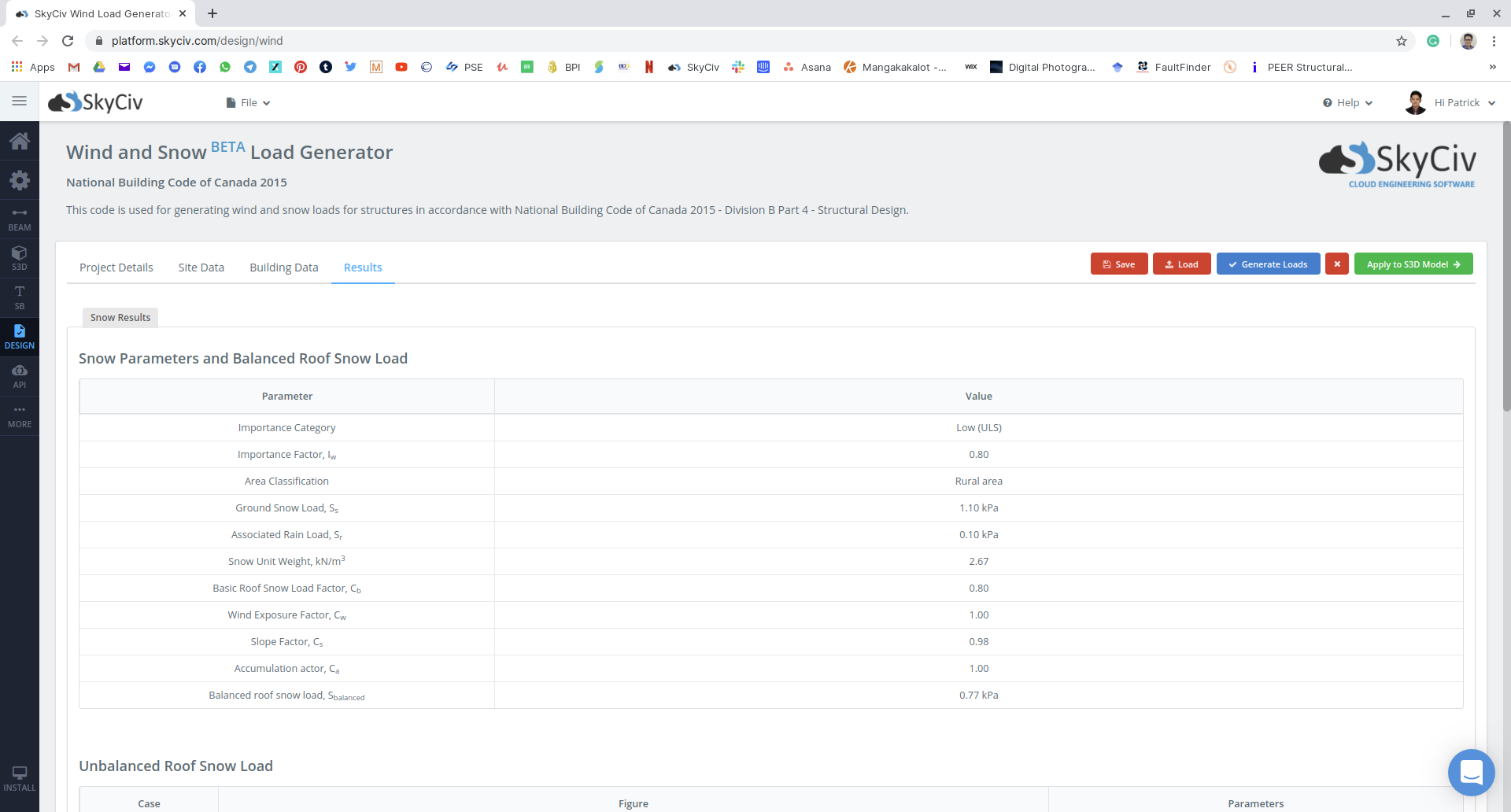
Figuur 18: Samenvatting van de gebruikte parameters voor sneeuwbelasting en de uitgebalanceerde sneeuwbelasting die op de constructie moet worden toegepast.
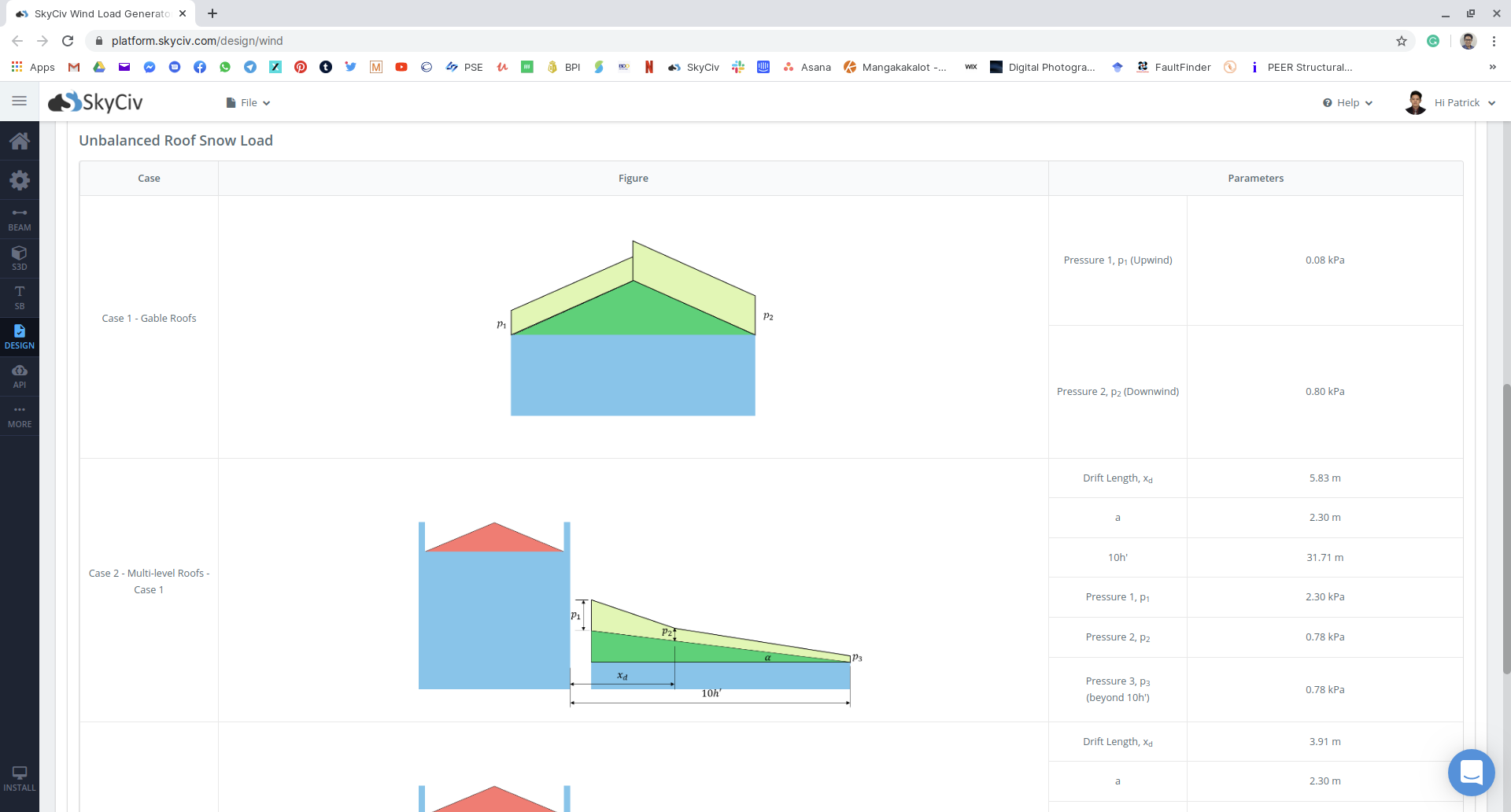
Figuur 19: Samenvatting van de resultaten van ongebalanceerde sneeuwbelasting.
Sneeuwbelastingberekeningen in de SkyCiv Load Generator-module worden ondersteund door referentiecodes zoals ASCE 7-10, 7-16, IN 1991-1-3, NBCC 2015, en AS/NZS 1170.3, en is beschikbaar op de Standalone (Alleen generator laden) en Professioneel rekeningen. Bekend met programmeren en API's? Deze functionaliteit kan worden geautomatiseerd met behulp van de SkyCiv API.
Bouwkundig ingenieur, Product ontwikkeling
MS Civiele Techniek
Referenties:
- Nationale Onderzoeksraad van Canada. (2015). Nationale bouwcode van Canada, 2015. Nationale Onderzoeksraad van Canada.
Notitie:
- NBCC-codereferentie voor de “Basis sneeuwbelastingsfactor voor daken” — zoeken 4.1.6.2 Zin (2)
- NBCC-codereferentie voor de “Windblootstellingsfactor” — zoeken 4.1.6.2 Zinnen (3) en (4)
- NBCC-codereferentie voor de “Hellingsfactor” — zoeken 4.1.6.2 Zinnen (5), (6), en (7)
- NBCC-codereferentie voor de “Accumulatiefactor” — zoeken 4.1.6.2 Zin (8), 4.1.6.5 voor daken met meerdere niveaus, 4.1.6.6 voor daken met spleet, en 4.1.6.9 voor zadeldaken



