Enkelpolig ontwerp volgens ACI 318 (2014)

Palen zijn lange en slanke elementen die de lasten van de bovenbouw overbrengen naar diepere grond of op een rots met voldoende draagvermogen. Materialen die voor palen worden gebruikt, kunnen hout bevatten, staal, en beton. Installatie van de paal in de grond kan worden geheid, geboord, of opgevijzeld die vervolgens worden verbonden met paalkappen. Veel factoren, zoals locatievoorwaarden, grondsoort, het overbrengen van lasten, worden beschouwd om het type en de installatie van palen te classificeren. Dit artikel richt zich op het ontwerpen van een betonnen paal in overeenstemming met het American Concrete Institute (ACI) 318 – 2014.

SkyCiv Foundation Design-module omvat het ontwerp van palen in overeenstemming met het American Concrete Institute (ACI 318) en Australische normen (NET ZO 2159 & 3600).

Wil je de Foundation Design-software van SkyCiv proberen?? Met onze gratis tool kunnen gebruikers lastdragende berekeningen uitvoeren zonder download of installatie!

Stichting ontwerp rekenmachine

Draagkracht van een paal

Over het algemeen, verticale belastingen op palen worden gedragen door het eindlager van de paal, en de huidwrijvingsweerstand ontwikkelde zich over de lengte ervan. Het ultieme draagvermogen (Q_U) wordt weergegeven door een vergelijking (1). Er wordt een veiligheidsfactor toegepast om het toelaatbare draagvermogen te berekenen (Q_EEN).

\({Q}_{u} = {Q}_{p} + {Q}_{s}\) (1)

Q_U = Ultiem draagvermogen

Q_P. = Eindlagerweerstand

Q_S = Huidwrijvingsweerstand

\({Q}_{EEN} = frac{{Q}_{U}}{FOS} \) (2)

Q_EEN = Toelaatbaar draagvermogen

FOS = Veiligheidsfactor

Voor een meer gedetailleerde gids, bekijk ons ​​artikel over rekenen de huidwrijvingsweerstand en het einddraagvermogen.

Structurele sterkte van een enkele paal

Palen worden ook onderworpen aan axiale krachten, afschuifkracht, en buigend moment, daarom zijn ze structureel vergelijkbaar met kolommen ontworpen. Sectie 10.5.1.1 stelt dat alle in rekening gebrachte belasting de overeenkomstige ontwerpsterkten niet mag overschrijden.

\( {øP}_{N} ≤ {P.}_{U} \) (3een)

\( {ontstoken}_{N} ≤ {M}_{U} \) (3b)

\( {øV}_{N} ≤ {V }_{U} \) (3c)

P._U, M_U, V _U = Axiaal gefactoreerd, buigend moment, schuifbelastingen

P._N, M_N, V _N = Nominaal axiaal, buigend moment, schuifbelastingen

ø = Krachtreductiefactoren (Tafel 1)

Krachtverminderingsfactoren(φ)
Axiaal	0.65-0.90
buigzaam	0.65-0.90
Schuintrekken	0.75

Tafel 1: Krachtverminderingsfactoren (Tafel 21.2.1, ACI 318-14)

Afschuifcapaciteit van een enkele paal (øV_N)

De nominale afschuifsterkte is gelijk aan de gecombineerde bijdragen van de afschuifcapaciteiten van beton- en staalwapening.

Afschuifsterkte van beton (V _c)

De bijdrage van beton aan de afschuifcapaciteit wordt berekend zoals weergegeven in de vergelijking (4) die is gedefinieerd op Sectie 22.5.5.1 van ACI 318-14.

\( {V }_{c} = 0.17 × λ × sqrt{fc’} × b × d \) (4)

λ = Concrete wijzigingsfactor = 1 (Normaal gewicht beton, Tafel 19.2.4.2)

fc’ = Sterkte van beton

b = paalbreedte of -diameter

d = 0.80 × paaldiepte (Sectie 22.5.2.2)

Afschuifsterkte van stalen staven (V _s)

De bijdrage van laterale afschuifwapening aan de afschuifcapaciteit wordt berekend als het minimum tussen de vergelijkingen (5) en (6).

\( {V }_{s} = 0.066 × sqrt{fc’} × b × d \) (5)

\( {V }_{s} = frac{{EEN}_{v} × {f}_{jt} × d }{s} \) (6)

EEN_V = Oppervlakte van de afschuifwapeningsstaven

f_jt = Vloeigrens van de afschuifwapeningsstaven

s = Hart op hart afstand van afschuifwapeningsstaven

Nominale afschuifsterkte (øV_N)

De uitvoer van de vergelijking optellen 4-6 resulteren in de nominale afschuifsterkte van de paal. Kracht reductie factor (O) zal gelijk zijn aan 0.75 zoals gedefinieerd in de tabel 22.2.1 van ACI 318-14.

\( {øV}_{N} = ø × ({V }_{c} + {V }_{s}) ≤ {øV}_{U} \) (7)

Stichting ontwerp rekenmachine

Axiale en buigcapaciteiten van een enkele paal (øP_N, ontstoken_N )

Axiale en buigcapaciteiten worden gecontroleerd met behulp van een interactiediagram. Dit diagram is een visuele weergave van het gedrag van de buig- en axiale capaciteiten veroorzaakt door een toename van de belasting vanaf het zuivere buigpunt totdat een evenwichtspunt is bereikt.

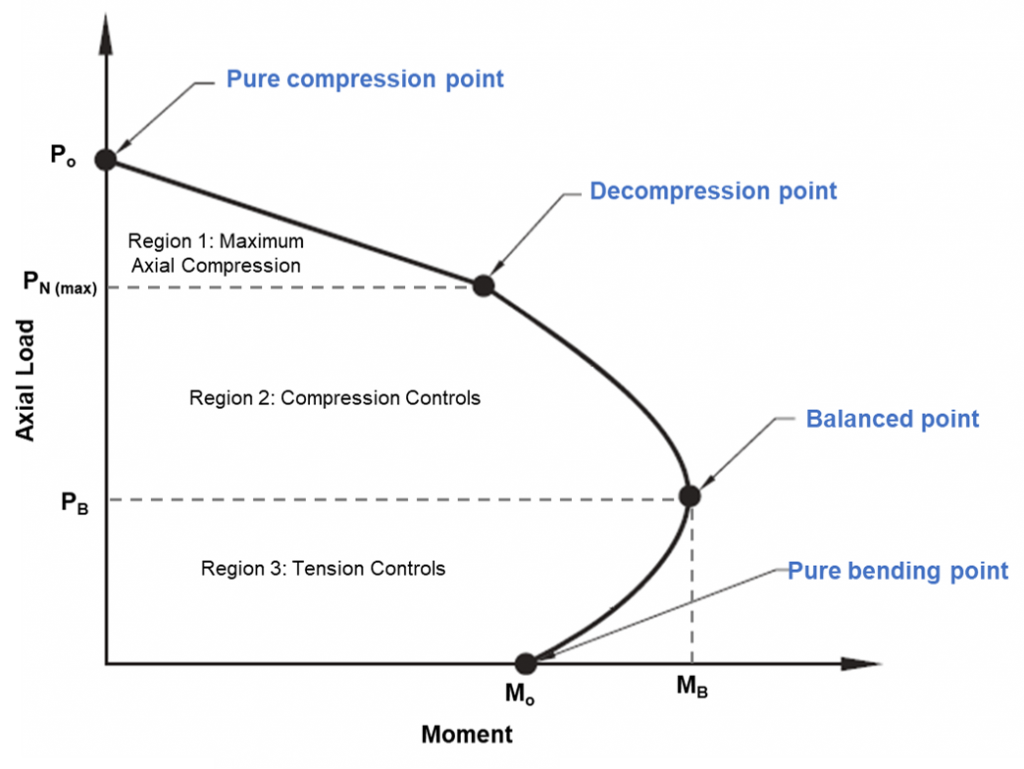
Figuur 1: Kolom-interactiediagram

Kolom interactie diagram

Het pure compressiepunt in het diagram is waar de paal puur niet zal worden samengedrukt. Op dit punt, de axiale belasting wordt uitgeoefend op het kunststof zwaartepunt van de sectie om samengedrukt te blijven zonder te buigen. De sterkte van de paal tussen het pure compressiepunt en de decompressiepunten kan worden berekend door lineaire interpolatie. Het decompressiepunt is waar de betonspanning bij de extreme drukvezel gelijk is aan 0.003, en de spanning in de vezel met extreme treksterkte is nul. Zuiver buigpunt is waar de axiale belastingscapaciteit nul is. Tussen de overgang van decompressiepunt naar puur buigpunt, een evenwichtige toestand wordt bereikt. Op dit punt, de betonspanning is aan zijn limiet (e_c=0.003), en de buitenste staalstam bereikt opbrengst (e_s=0,0025). Elke combinatie van axiale belasting en buigmoment buiten het diagram zal falen veroorzaken.

Maximale nominale axiale druksterkte voor ontwerp (øP_N)

De ontwerpaxiale sterkte van een sectie zal slechts worden beperkt tot 80-85% van de nominale axiale sterkte om rekening te houden met toevallige excentriciteit.

\( {øP}_{N} = ø × {P.}_{De} \) (8een)

\( {P.}_{De} = F × [0.85 × {f}_{c} × ({EEN}_{g} – {EEN}_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak}) + ({f}_{en} × {EEN}_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak}) ] \) (8b)

F = 0.80 (Stropdassen)

F = 0.85 (Spiraal)

EEN_G = Bruto oppervlak van de paaldoorsnede

EEN_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak} = Totale oppervlakte van de stalen langsstaven

f_en = Rekgrens van stalen staven

Nominale buigsterkte (ontstoken_N)

De constructie van het interactiediagram voor de kolom omvat het plotten van een reeks waarden van P_N en M_N. Waarden voor P_N moet gelijk zijn aan de som van de trek- en drukkrachten, zoals getoond in figuren 2a en 2b, terwijl de corresponderende M_N wordt berekend door deze krachten om de neutrale as op te lossen. Deze krachten omvatten de drukkracht die op het drukgebied inwerkt en de krachten die worden uitgeoefend door elk van de wapeningsstaven, die zowel druk- als trekkrachten kunnen zijn.. Hieronder wordt een algemene procedure voorgesteld om een ​​interactiediagram te construeren met behulp van de gepresenteerde vergelijkingen.

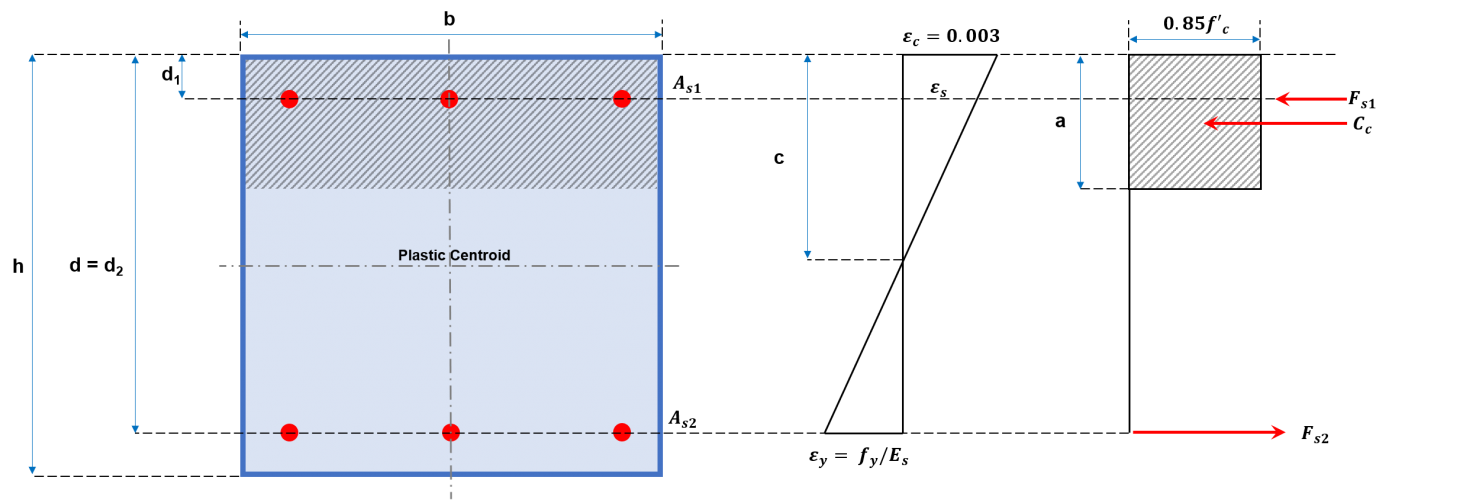
Figuur 2a: Rechthoekige kolomdoorsnede

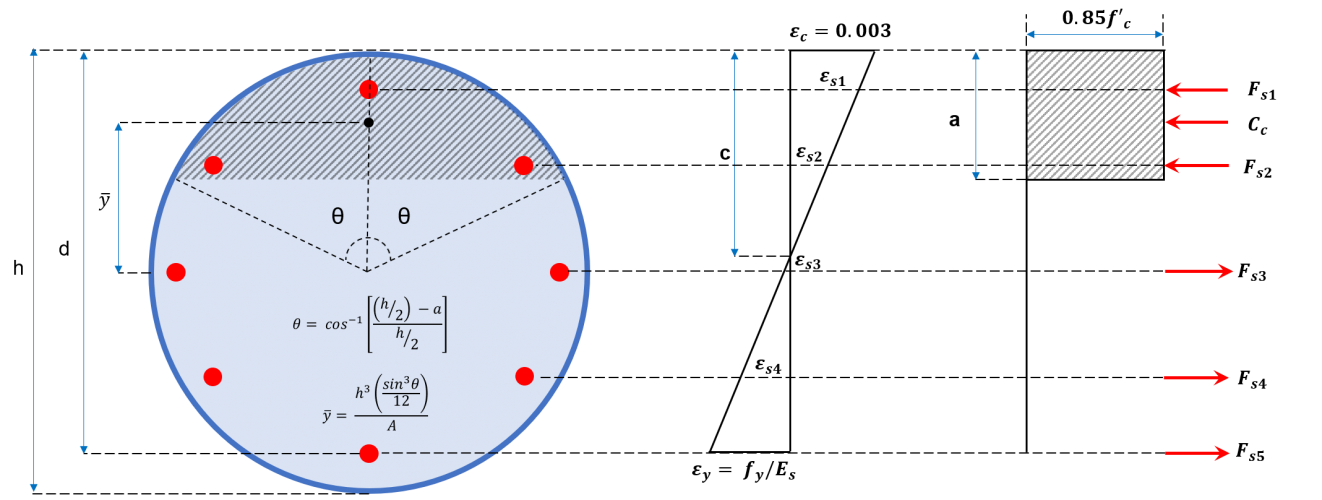
Figuur 2b: Cirkelvormige kolomdoorsnede

Algemene procedure voor interactiediagram van een kolom

(1) Bereken voor de waarde van P_De en P_N (vergelijkingen 8a en 8b).

(2) Bepaal c en de spanningen in de wapeningen.

\( c = 0.003 × frac{{d}_{1}}{0.003 + (MET + {e}_{en})} \) (9)

c = Neutrale asdiepte

e_en = Spanning van staal = f_en/E_s

Z = Willekeurige waarde (0, -0.5, -1.0, -2.5)

Een reeks gevallen wordt overwogen door verschillende locaties van de neutrale as te selecteren, c. Om de locaties van de neutrale as in te stellen, verschillende staalspanningen moeten worden geselecteerd door een willekeurige waarde Z te vermenigvuldigen met de vloeigrens van het staal. Er is een breed scala aan waarden voor Z. Echter, er zijn slechts vier verplichte punten om te gebruiken voor het interactiediagram.

• Z = 0: op dit punt, de rek bij de uiterste spanningslaag is nul. Dit punt markeert de overgang van een overlappende compressieverbinding die is toegestaan ​​op alle langsstaven naar een overlappende spanningsverbinding.
• Z = -0.5: deze spanningsverdeling is van invloed op de lengte van de trekoverlapping in een kolom & wordt gewoonlijk uitgezet op een interactiediagram.
• Z = -1: dit markeert het punt van een evenwichtige toestand. Deze spanningsverdeling markeert de verandering van compressiefouten die ontstaan ​​door het samendrukken van het compressieoppervlak van de sectie naar spanningsfouten die worden geïnitieerd door de vloei van de langswapening.
• Z = -2.5: dit punt komt overeen met de spanningsgestuurde spanningslimiet van 0.005.

(3) Bereken voor de spanningen in de wapeningslagen.

\({f}_{En} ={e}_{En} × {E}_{s} \) (10)

f_En = Spanning in staal

e_En = Spanning in staal

\({e}_{En} = frac{c -{d}_{ik}}{c} × 0.003 \) (11)

E_s = Elasticiteitsmodulus van staal

(4) Bepaal de hoogte van het drukspanningsblok, een.

\(a = {b}_{1} × c \) (a ≤ h)(12)

Voor f’c ≤ 4000 psi (28 MPa):

b₁ = 0.85

Voor f'c > 4000 psi (28 MPa):

\( {b}_{1} = 0.85 – \frac{0.05 × (f'c – 4000)}{1000} \) (Imperial)

\( {b}_{1} = 0.85 – \frac{0.05 ×(f'c – 28)}{7} \) (Metriek)

(5) Bereken de krachten in beton en staal.

Gebied van het drukspanningsblok:

\({EEN}_{c} = een × b \) (Rechthoekige doorsnede)

\({EEN}_{c} ={h}^{2} × frac{θ – sinθ cosθ}{4} \) (Cirkelvormige doorsnede)

Drukkracht in beton:

\({C}_{c} = (0.85 × f’c) × {EEN}_{c}\) (14)

Trekkracht in staal (d_ik≤ een):

\({F}_{En} = {f}_{En} × {EEN}_{En} \) (15)

Drukkracht in staal (d_ik > een):

\({F}_{En} = [{f}_{En} – (0.85 × f’c)] × {EEN}_{En} \) (16)

(6) Bereken voor de axiale capaciteit (P._N).

\({P.}_{N} = {C}_{c} + S {F}_{En} \) (17)

(7) Bereken voor de buigcapaciteit (M_N).

\({M}_{N} = [{C}_{c} × (\frac{h}{2} – \frac{een}{2})]+ S [{F}_{En} × (\frac{h}{2} – {d}_{ik}) \) (18)

(8) Bereken voor de waarde van de sterktereductiefactor (O).

Zoals weergegeven in de tabel 1, de sterktereductiefactor voor zowel axiaal als buiging varieert van 0.60 naar 0.90. Sectie 21.2 van ACI 318-14 bewijst voorlopig zijn waarde, axiale kracht, of gecombineerd moment en axiale kracht, zoals weergegeven in de tabel 2 hieronder.

Classificatie	Spiraal	Gebonden
Compressie gecontroleerd	0.75	0.65
Overgang van compressie naar spanning	0.75 + [50 × (et – 0.003) ]	0.65 + [(250/3) × (et – 0.003) ]
Spanning gecontroleerd	0.90	0.90

Tafel 2: Krachtverminderingsfactoren voor axiaal, moment of combineer axiaal en moment (Tafel 21.2.2, ACI 318-14)

(9) Herhaal de stappen 2-8 met verschillende waarden voor Z.

(10) Plot in het diagram de waarden van øP_N en øM_N.

Ontwerp van betonnen palen met SkyCiv Free Foundation Calculator

SkyCiv Gratis Foundation-calculator helpt u bij het ontwerpen van betonpalen en andere taken zoals het ontwerpen van funderingen en betonpalen. Bekijk het nu om te ontdekken hoe onze calculator u kan helpen met uw betonpaalproject!

Stichting ontwerp rekenmachine

Referenties

• • Bouwvereisten voor constructief beton (2014). AC! 318-14 Amerikaans Betoninstituut.
  • Hsiao, JK. (2012). Buig-aseffecten op belastingsmoment (P.M) Interactiediagrammen voor ronde betonnen kolommen met een beperkt aantal longitudinale wapeningsstaven. Elektronisch tijdschrift voor bouwtechniek 12 (1). Opgehaald van http://www.ejse.org