Inhoudsopgave
- Soorten ondersteuningen en hun reacties
- Een stapsgewijze handleiding voor het bepalen van de ondersteuningsreacties in balken
- SkyCiv Beam-software
Soorten ondersteuningen en hun reacties
Het is belangrijk om ook de verschillende soorten ondersteuningen te begrijpen en welke reacties ze produceren in uw analysemodel. Hieronder vindt u een kort spiekbriefje van de verschillende ondersteuningstypes en hun reacties:
| Type ondersteuning | Vertaling | Rotatie | Opmerkingen |
|---|---|---|---|
Vaste ondersteuning |
Gefixeerd in alle richtingen Reacties in X,EN,MET |
Gefixeerd in alle richtingen Reacties in X,EN,MET |
FFFFFF – Reacties in alle vrijheidsgraden |
Horizontale rolsteun |
Vast in Y Reacties alleen in Y-richting |
Vrijgegeven in alle richtingen Geen rotatiereacties |
RFFRRR – Reacties zijn alleen in de Y-richting |
Vastgezette of scharnierende ondersteuning |
Vast in X,EN,MET Reacties in X,EN,MET |
Vrijgegeven in alle richtingen Geen rotatiereacties |
FFFRRR – Reacties in alle vertalingen, geen in rotatie |
| Vrijdragende ondersteuning |
Gefixeerd in alle richtingen Reacties in X,EN,MET |
Gefixeerd in alle richtingen Reacties in X,EN,MET |
Hetzelfde als vast |
Een stapsgewijze handleiding voor het bepalen van de ondersteuningsreacties in balken:
Het bepalen van reacties op steunen is altijd de eerste stap bij het analyseren van een liggerconstructie, en het is over het algemeen het gemakkelijkst. Het omvat het berekenen van de reactiekrachten op de steunen (ondersteunt A en B in het onderstaande voorbeeld) vanwege de krachten die op de balk werken. U moet dit weten om door te gaan en te berekenen buigmoment diagrammen (BMD's) en dwarskracht diagrammen (SFD's); een belangrijk onderdeel van uw statica en structurele hbo / universitaire opleidingen. SkyCiv biedt een krachtig Gratis reactiecalculator waarmee u elke straal kunt modelleren en deze handberekeningen voor u kunt laten zien, maar het is ook een belangrijk concept om te begrijpen.
Video uitleg: Bepaal de reacties bij de steunen
Bij het oplossen van een dergelijk probleem willen we eerst onthouden dat de straal statisch is; wat betekent dat het niet beweegt. Van eenvoudige natuurkunde, dit betekent dat de som van de krachten in de y-richting gelijk is aan nul (d.w.z. de totale neerwaartse krachten zijn gelijk aan de totale opwaartse krachten). Een tweede formule om te onthouden is dat de som van de momenten op een bepaald punt gelijk is aan nul. Dit komt doordat de straal statisch is en dus niet roteert.
Om de reacties op steunen te bepalen, volg deze eenvoudige stappen:
1. Som van momenten (ΣM = 0)
Alles wat we in dit stadium over momenten moeten weten, is dat ze gelijk zijn aan de kracht vermenigvuldigd met de afstand vanaf een punt (d.w.z. de kracht x afstand vanaf een punt). Beschouw een eenvoudig voorbeeld van een 4 meter lange balk met een pinsteun bij A en een rolsteun bij B. Het free-body-diagram wordt hieronder weergegeven, waarbij Aen en Ben zijn de verticale reacties op de steunen: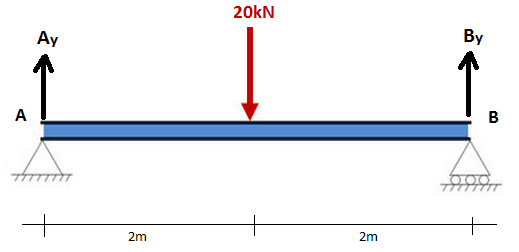
We willen eerst de som van momenten rond punt B bekijken en deze gelijk aan nul stellen. We hebben punt B gekozen om te bewijzen dat dit aan beide uiteinden van de balk kan worden gedaan (mits het pin ondersteund). Echter, je zou net zo goed vanuit punt A kunnen werken. Zo, nu tellen we de momenten rond punt B op en laten we de som gelijk zijn 0:
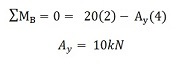
NOTITIE: De tekenconventie die we hebben gekozen, is dat momenten tegen de klok in positief zijn en momenten met de klok mee negatief zijn. Dit is de meest voorkomende tekenconventie, maar het is aan jou. U moet tijdens de hele opgave ALTIJD dezelfde tekenconventie gebruiken. Gebruik altijd vanaf het begin dezelfde tekenconventie. We hebben nu onze eerste vergelijking. We moeten nog een vergelijking oplossen om B te vindenen (de verticale reactiekracht op steunpunt B).
2. Som van horizontale krachten (ΣFen = 0)
Tel de krachten in de y op (verticaal) richting en laat de som gelijk zijn aan nul. Denk eraan om alle krachten op te nemen, inclusief reacties en normale belastingen zoals puntbelastingen. Dus als we de krachten in de y-richting optellen voor het bovenstaande voorbeeld, we krijgen de volgende vergelijking:
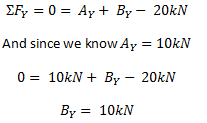
NOTITIE: Opnieuw hielden we vast aan een tekenconventie die opwaartse krachten moest opnemen (onze reacties) als positieve en neerwaartse krachten (de puntbelasting) als negatief. Onthoud dat de tekenconventie aan jou is, maar je moet ALTIJD dezelfde tekenconventie gebruiken tijdens het hele probleem.
Dus daar hebben we het, we hebben de twee bovenstaande vergelijkingen gebruikt (som van momenten is gelijk aan nul en som van verticale krachten is gelijk aan nul) en berekend dat de reactie op drager A is 10 kN en de reactie op drager B 10kN. Dit is logisch aangezien de puntbelasting precies in het midden van de balk ligt, wat betekent dat beide steunen dezelfde verticale krachten moeten hebben (d.w.z. het is symmetrisch).
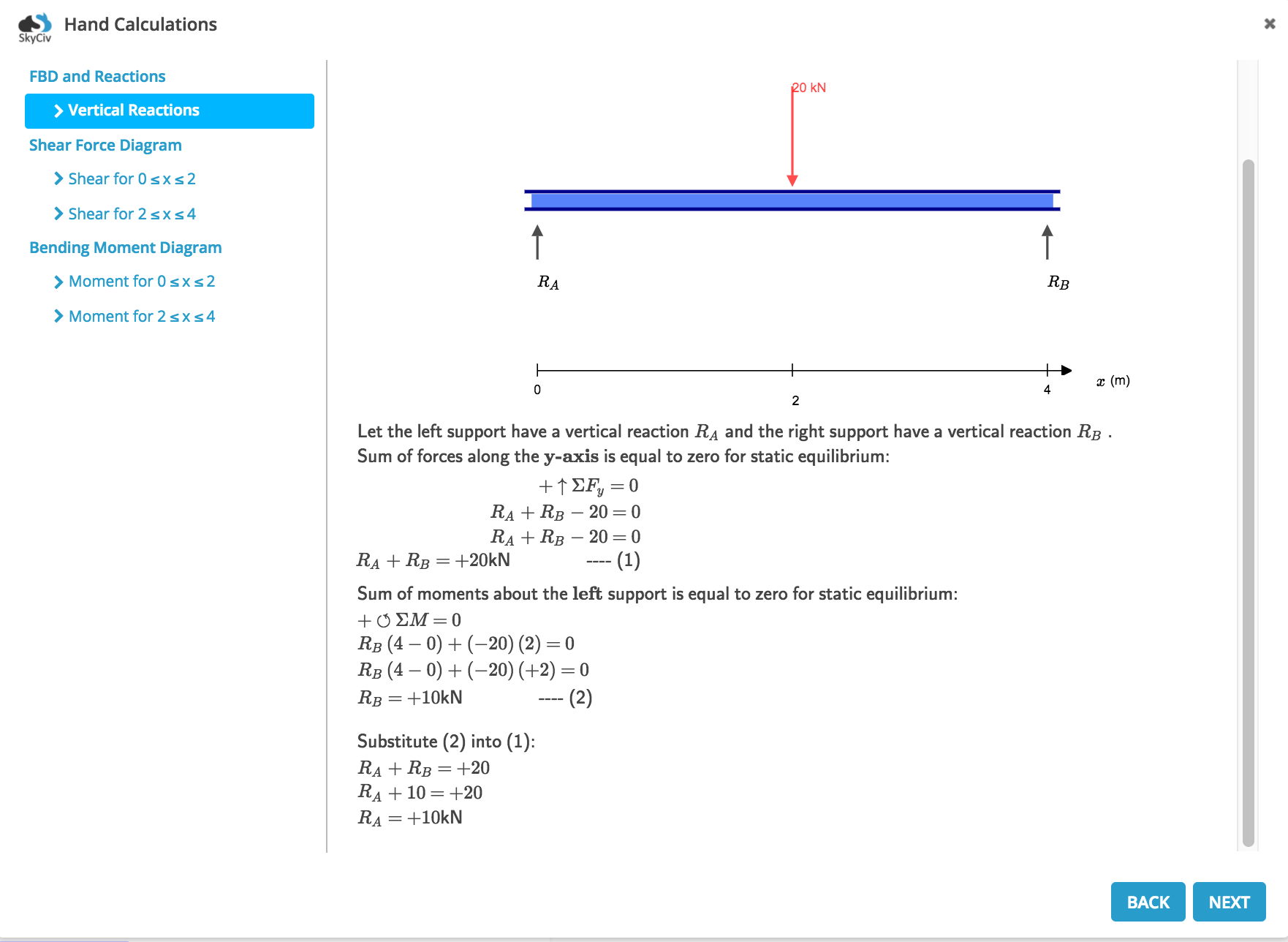
samengevat, hier zijn de volledige hand berekeningen gemaakt door SkyCiv Beam:
SkyCiv Beam-software
Via dit artikel, je hebt het concept van reactiekrachten op de steunen geleerd. SkyCiv Beam-analysesoftware stelt gebruikers in staat om balkstructuren gemakkelijk en nauwkeurig te analyseren. U kunt een analyse van uw ligger krijgen, inclusief reacties, afschuifkracht, buigend moment, afbuiging, benadrukt, en onbepaalde liggers in een kwestie van seconden.
Als je het eerst wilt proberen, Gratis Beam Calculator is een geweldige manier om te beginnen, of meld je vandaag nog gratis aan!
