Overzicht

Buigspanning is een van de belangrijkste waarden bij constructief ontwerp, Zoals voor de meeste horizontale balken is dit typisch een kritisch of bepalend ontwerp. Omdat een horizontale balk wordt belast, het genereert buigmoment spanningen in de bovenste en onderste vezels van de sectie, waardoor de sectie overbelast kan raken, waardoor deze kan bezwijken of volledig kan bezwijken.

Bij het berekenen van buigspanning, Het is belangrijk om het volgende te overwegen:

1. Traagheidsmoment van uw sectie – heeft rechtstreeks invloed op de buigspanning
2. Waar op de balk u controleert – de buigspanning neemt doorgaans toe naarmate u zich verder van de neutrale as van de sectie verwijdert (vandaar dat de spanningen bovenaan en onderaan de sectie het grootst zijn)
3. De materiaaleigenschappen – sterkere materialen (hogere vloeigrens bijvoorbeeld) is bestand tegen hogere spanningen en kan in bepaalde ontwerpen geschikter zijn
4. Vormen van dwarsdoorsneden – zoals bij punt (1) bovenstaande – verschillende secties zijn goed geschikt om hogere buigspanningen te weerstaan, gezien hun hogere traagheidsmomentwaarden
5. Richting van de spanning – buiging kan optreden in zowel de hoofd- als de nevenas van een sectie, afhankelijk van de richting van de belasting.
6. Vaak, deze buigspanningen kunnen worden gecombineerd met schuif- of axiale spanningen (door krachten in andere richtingen), het verhogen van de algehele spanning in een balk

In de volgende gids zullen we vooral onderzoeken hoe we de buigspanning kunnen berekenen (vooral in een I Beam), maar het is belangrijk om de bovenstaande context in gedachten te houden bij het leren van deze principes.

Hoe bereken je buigspanningen in balken?

Het begrijpen van buigspanningen is belangrijk omdat balkbuiging een cruciale rol speelt in het ontwerp van balken. Deze tutorial laat zien hoe je buigspanningen in een balk kunt berekenen met een formule. Deze formule relateert de longitudinale spanningsverdeling in een balk aan het interne buigmoment dat werkt op de doorsnede van de balk. We gaan ervan uit dat het materiaal van de balk lineair-elastisch is (d.w.z. De wet van Hooke is van toepassing).

1. Bereken Buigspanningen Met de Hand Met Buigspanningsformules (Vergelijkingen)

Laten we een voorbeeld bekijken. Overweeg de getoonde I-balk hieronder:

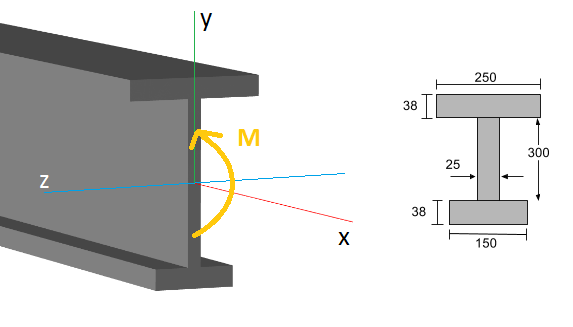
Op een specifiek punt langs de lengte van de balk (de x-as), bestaat er een intern buigmoment (M), dat normaal wordt bepaald met behulp van een buigmomentdiagram. De algemene buigspanningsformule (of normale spanning) op de sectie staat:

Wanneer we een specifieke sectie van een balk beschouwen, wordt het duidelijk dat de buigspanning zijn maximale waarde zal bereiken op een specifieke afstand van de neutrale as (j). Dus, de maximale buigspanning zal optreden aan de boven- of onderkant van de balksectie, afhankelijk van welke afstand groter is:

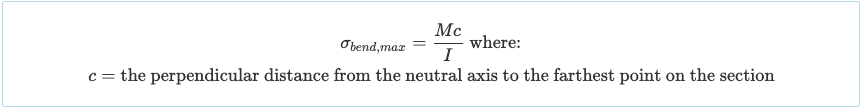
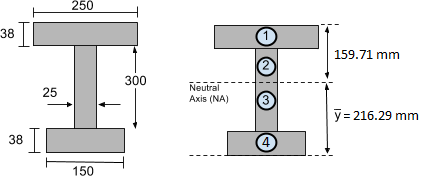
Laten we het werkelijke voorbeeld van onze I-balk hierboven bekijken. In onze vorige traagheidsmoment-tutorial, hebben we al het traagheidsmoment rond de neutrale as gevonden, dat I = 4,74×10⁸ mm⁴. Bovendien, hebben we in de zwaartepunt tutorial, het zwaartepunt en daarmee de locatie van de neutrale as bepaald op 216.29 mm van de onderkant van de sectie. Dit wordt hieronder weergegeven:

Het is meestal nodig om de maximale buigspanning te bepalen die door een sectie wordt ervaren. Bijvoorbeeld, laten we bijvoorbeeld aannemen dat we, uit het buigmomentdiagram, hebben bepaald dat de balk een maximaal buigmoment van 50 kN-m of 50,000 Nm (na het omzetten van de buigmoment-eenheden).

Dan moeten we bepalen of de bovenkant of onderkant van de sectie verder van de neutrale as af is. Duidelijk, is dat de onderkant van de sectie een grotere afstand heeft, namelijk c = 216.29 mm. Met deze informatie, we kunnen doorgaan met het berekenen van de maximale spanning door de hierboven gegeven buigspanningsformule te gebruiken:

Evenzo, kunnen we de buigspanning aan de bovenkant van de sectie vinden, aangezien we weten dat deze y = 159.71 mm van de neutrale as is (NA):

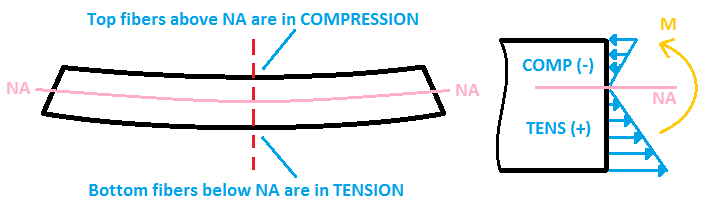
De laatste overweging omvat het bepalen of de balkspanning compressie of trekspanning veroorzaakt in de vezels van de sectie.

• Als de balk doorbuigt in de vorm van een “U” vorm, ondergaan de bovenste vezels compressie (negatieve spanning), terwijl de onderste vezels trekspanning ondergaan (positieve spanning).
• Als de balk doorbuigt in een omgekeerde “U” vorm, is de situatie omgekeerd: de onderste vezels worden aan compressie onderworpen, terwijl de bovenste vezels trekspanning ondergaan.

2. Bereken Buigspanningen met Software

In het bovenstaande gedeelte is de buigspanningsformule voor handmatige berekening besproken, maar je hoeft het niet langer zelf handmatig te doen als de SkyCiv Beam Calculator kan u helpen met één klik schuif- en buigspanningen in een balk te vinden. Door eenvoudigweg de balk te modelleren, steunpunten op te nemen, en belastingen toe te passen, kun je de maximale spanningen vinden met deze buigspanningscalculator. De onderstaande afbeelding toont een voorbeeld van een I-balk die buigspanningen ondervindt:

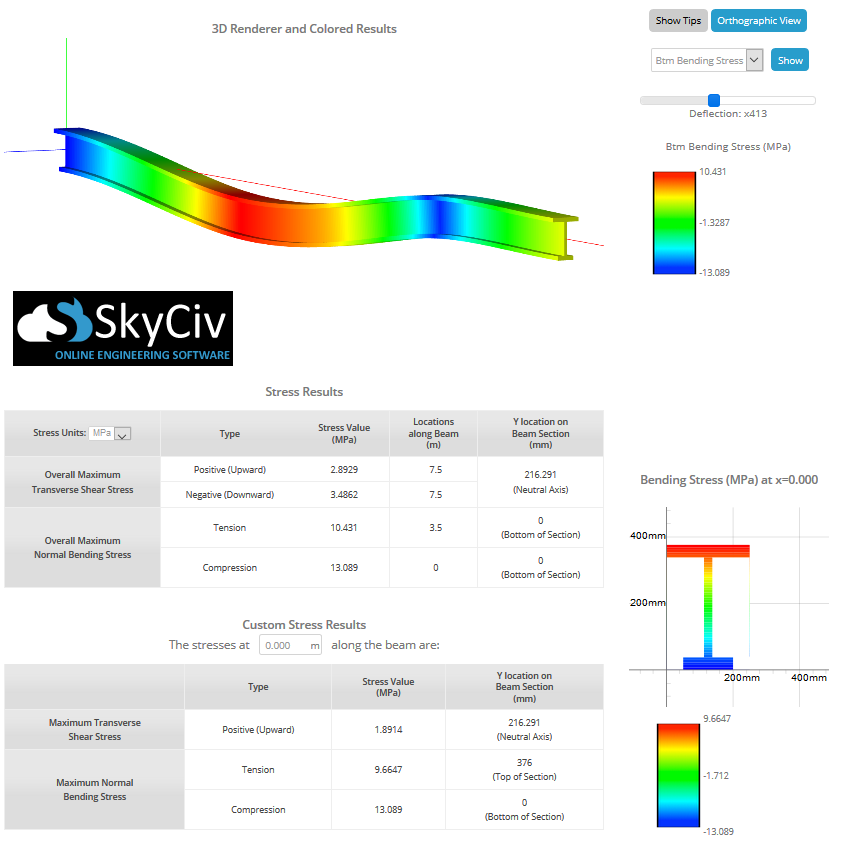
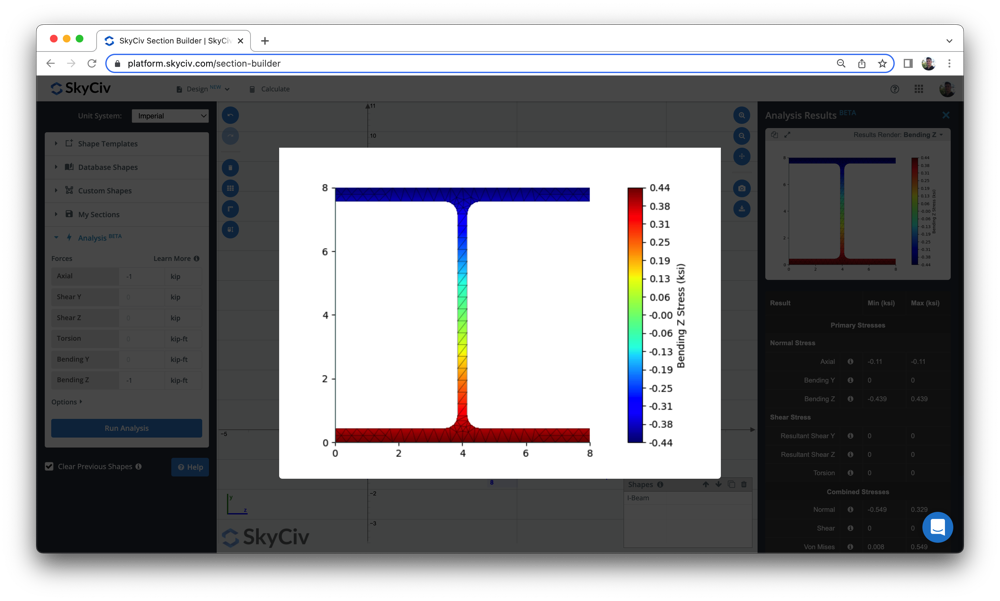
Gebruikers kunnen ook de volgende Balkspanningssoftware gebruiken om de buigspanning en andere spanningen in balken te berekenen, met behulp van een eenvoudig sectie-bouwgereedschap. Bekijk onze balktool hierboven of meld je vandaag nog aan om de software gratis uit te proberen!

Ga gratis aan de slag

Voor meer documentatie over balken, bekijk onze artikelen over het berekenen van de buigspanning van een balksectie, hoe je buigmomenten kunt vinden, de reacties bij de steunpunten kunt bepalen, en en de doorbuiging van balken kunt berekenen.