Zelfstudie: Hoe een truss-structuur op te lossen met behulp van de sectiemethode

In deze tutorial, we zullen de voordelen onderzoeken en leren van het gebruik van de methode van secties om uw truss-structuur op te lossen. Wat zijn trossen? Als u hier niet zeker van bent, bezoek onze Wat is een truss artikel. De methode van secties wordt gebruikt om grotere truss-structuren snel op te lossen, eenvoudige manier. Het omvat het nemen van een ‘snee’ door een aantal leden om hun axiale krachten te evalueren en dit als onze basis te gebruiken om de rest van de truss-structuur op te lossen.

Het mooie is, SkyCiv Truss doet dit automatisch voor je. Modelleer uw eigen spanten en de software zal interactieve stap-voor-stap uitwerken van de methode van secties laten zien!

Bekijk de video-tutorial

Voorbeeldvraag

Voor ons uitgewerkte voorbeeld, we zullen de volgende vraag bekijken::

Vraag: Met behulp van de methode van secties, bepaal de krachten in leden 10, 11, en 13 van de volgende truss-structuur:

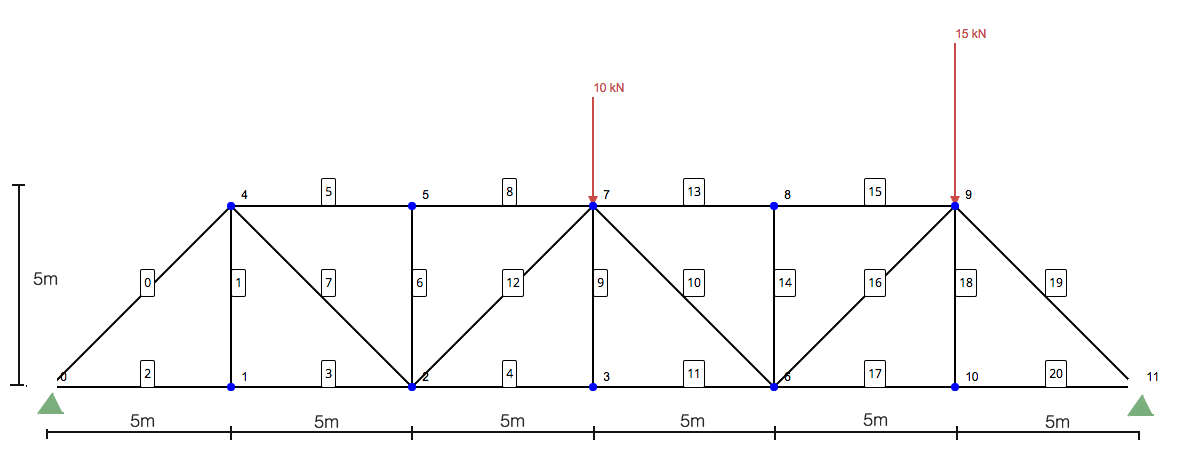
Stap 1: Bereken de reacties op de steunen

Zoals de meeste statische structurele analyses, we moeten eerst beginnen met het lokaliseren en oplossen van de eacties bij steunpunten. Dit geeft ons de randvoorwaarden die we nodig hebben om vooruitgang te boeken bij het oplossen van de truss-structuur. Vereenvoudiging van de structuur door alleen de belastingen en steunen op te nemen:

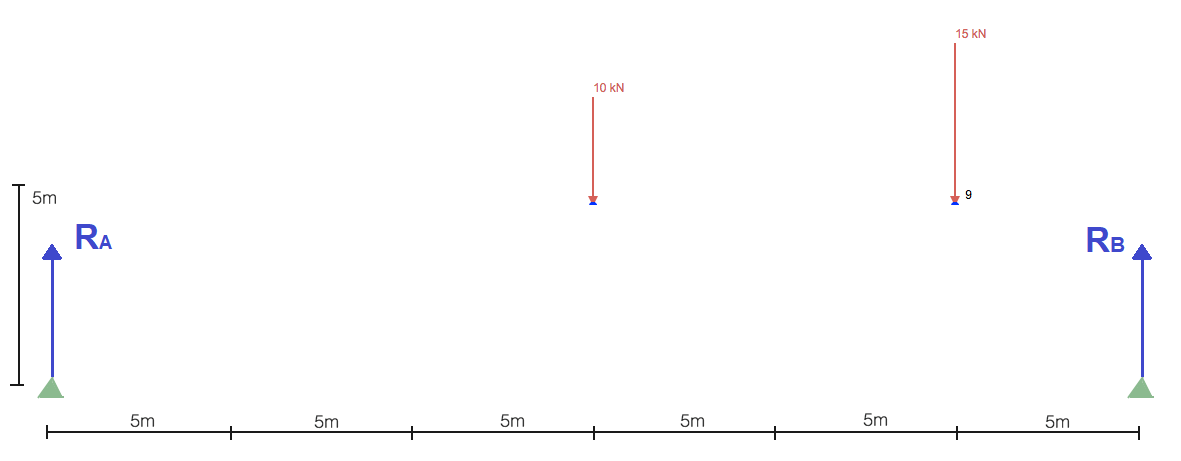
Zonder al te veel tijd te besteden aan het berekenen van de reacties, je begint over het algemeen met de som van momenten over een punt. Door de som van momenten over de linkse steun te nemen, krijgen we ons:

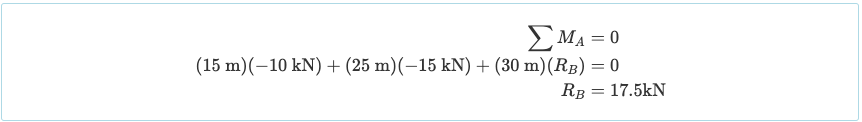
Dus de reactie bij de juiste ondersteuning (R_B) is 17.5 kN in opwaartse richting. Nu, het nemen van de som van de krachten in de y geeft ons de reactie R_A als 7,5 kN in opwaartse richting:

Stap 2: Maak een snee langs de leden van belang

Hier komt het belangrijkste onderdeel van het oplossen van een truss met behulp van de methode van secties:. Het gaat om het doorsnijden van de leden die u wilt oplossen. Deze methode van structurele analyse is uitermate handig wanneer u probeert om enkele staven op te lossen zonder de hele constructie op te lossen met behulp van de verbindingsmethode. Dus, in ons voorbeeld zou hier onze plak zijn:

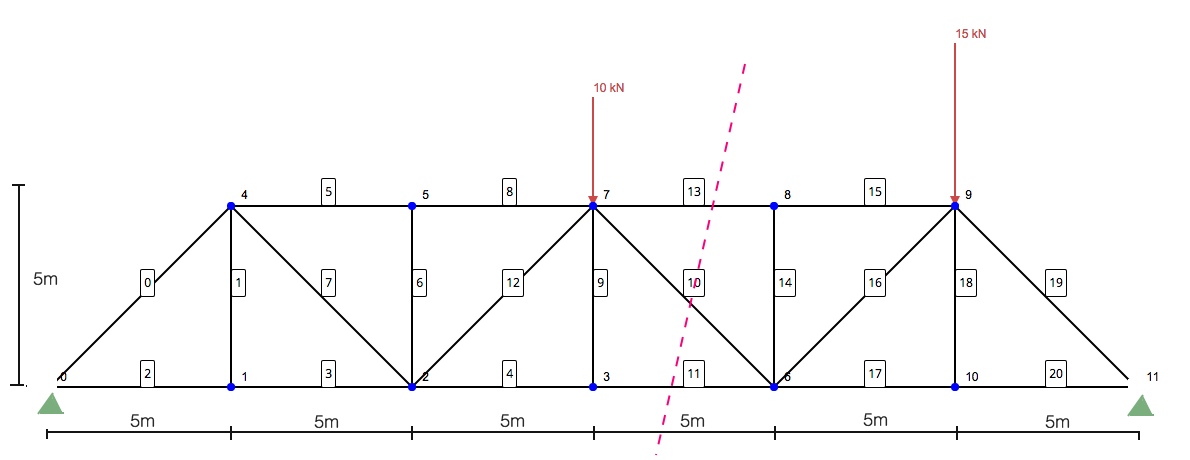
Alleen aan de linkerkant scherpgesteld, je blijft achter met de volgende structuur:

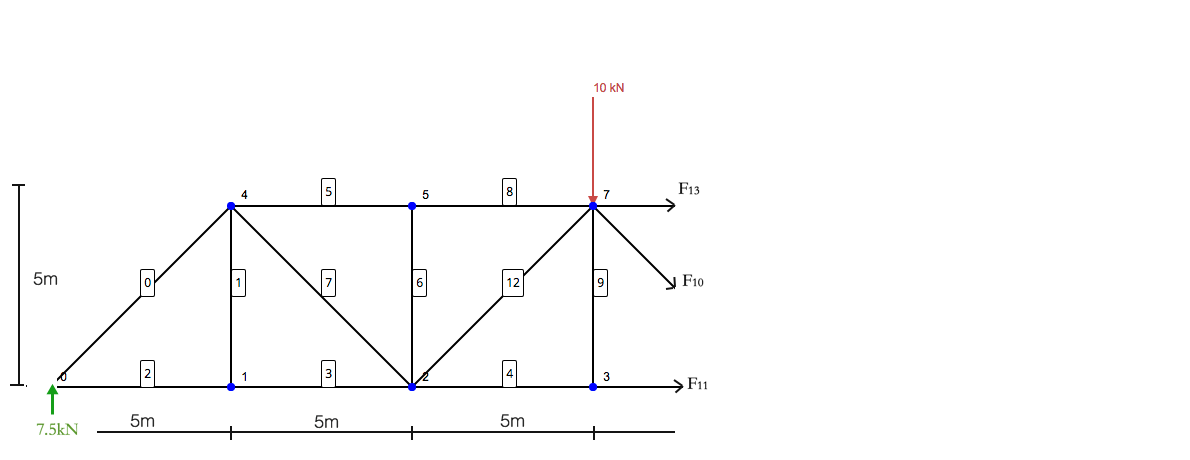
Beschouw deze structuur nu als een enkele staande structuur. De wetten van de statica zijn nog steeds van toepassing – dus de som van momenten en krachten moet allemaal gelijk zijn aan nul. De leden met pijlen (F₁₃, F₁₀, F₁₁) zijn wat de reactie en krachten die op de constructie worden uitgeoefend, stabiliseren. Merk op dat de som van de momenten wordt genomen over het knooppunt 7 – zoals de krachten van leden zou uitsluiten 13 en 10 – het verlaten van F₁₁ geïsoleerd te zijn.

Met behulp van het bovenstaande Free Body-diagram, we kunnen de volgende formules verkrijgen:

Som van krachten in de y-richting:

[wiskunde]
\beginnen{uitlijnen}
+\pijl omhoog tekst{ } \som{F_y} &= 0\\
7.5\tekst{ kN} – 10 \tekst{ kN} – F_{10}zonder(45^{\omg}) &= 0\\
F_{10} &= -3.536 \tekst{ kN}
\einde{uitlijnen}
[wiskunde]

Som van momenten over knooppunt 7:

[wiskunde]
\beginnen{uitlijnen}
+\cirkelpijllinks text{ } \som{M_7} &= 0\\
-(15 \tekst{ m})(7.5 \tekst{ kN}) + (5 \tekst{ m})F_{11} &= 0\\
F_{11} &= 22.5 \tekst{ kN}
\einde{uitlijnen}
[wiskunde]

Som van krachten in de x-richting:

[wiskunde]
\beginnen{uitlijnen}
+\pijl naar rechts tekst{ } \som{F_x} &= 0\\
F_{13} + F_{11} + F_{10}omdat(45^{\omg}) &= 0\\
F_{13} &= -F_{11} – F_{10}omdat(45^{\omg}) \\
F_{13} &= – (22.5 \tekst{ kN}) – (-3.536 \tekst{ kN})omdat(45^{\omg}) \\
F_{13} &= -22.5 \tekst{ kN} + (3.536 \tekst{ kN})omdat(45^{\omg}) \\
F_{13} &= -20 \tekst{ kN}
\einde{uitlijnen}
[wiskunde]

Uiteindelijke oplossing

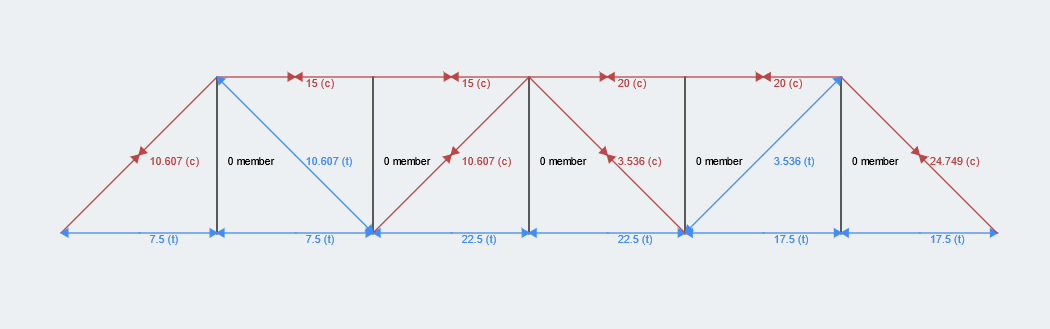
We kunnen deze resultaten gebruiken om de resterende leden in de truss-structuur op te lossen. We hopen dat dit voorbeeld van een truss-berekening nuttig is geweest en voel je vrij om hieronder je vragen te stellen. Als een referentie, de resultaten voor de gehele Truss-constructie vindt u hieronder (met behulp van onze Spant Calculator) wat geweldig is om uw antwoorden te controleren!

Samenvatting van stappen

• Begin altijd met het berekenen van reacties op ondersteuningen
• Snijd door de leden die u wilt oplossen
• Behandel de halve structuur als zijn eigen statische truss
• Los de truss op door de som van de krachten = te nemen 0
• Neem het moment over een knooppunt van meer dan één onbekend lid

SkyCiv Truss-software

We hopen dat je deze tutorial nuttig vond voor je projecten. Bezoek onze truss-tutorials voor meer nuttige informatie over truss en vergeet niet om onze gids voor het oplossen van truss door Method of Joints.

SkyCiv Truss kan de methode van secties automatisch voor u berekenen. Of probeer onze Gratis Truss Calculator die je het definitieve antwoord zal geven (geen handberekeningen).

Om meer functionaliteit van SkyCiv-software te verkennen, meld je vandaag nog aan om te beginnen!

Ga gratis aan de slag