Inhoudsopgave
- Wat is een cantileverbalk?
- Vrijdragende balkvergelijkingen en handmatige berekeningen
- Ontwerp met vrijdragende balk
- Cantilever Beam-software
Cantilever Beam-definitie: Wat is een cantileverbalk?
Een vrijdragende balk is een structureel element dat zich horizontaal uitstrekt en slechts aan één uiteinde wordt ondersteund. Het niet-ondersteunde uiteinde staat bekend als de cantilever, en het reikt verder dan het steunpunt. Vrijdragende balken worden vaak gebruikt in de bouw om balkons te ondersteunen, daken, en andere overhangen. Ze kunnen ook worden gebruikt in bruggen en andere constructies om het dek uit te breiden over een waterweg of ander obstakel.
Vrijdragende liggers zijn staven die slechts aan één zijde worden ondersteund – meestal met vaste ondersteuning. Om ervoor te zorgen dat de structuur statisch is, de steun moet zo worden bevestigd dat hij alle krachten en momenten in alle richtingen kan dragen. Een vrijdragende ligger wordt meestal zo gemodelleerd, waarbij het linkeruiteinde de steun is en het rechteruiteinde het vrijdragende uiteinde:

Cantilever Beam-vergelijkingen
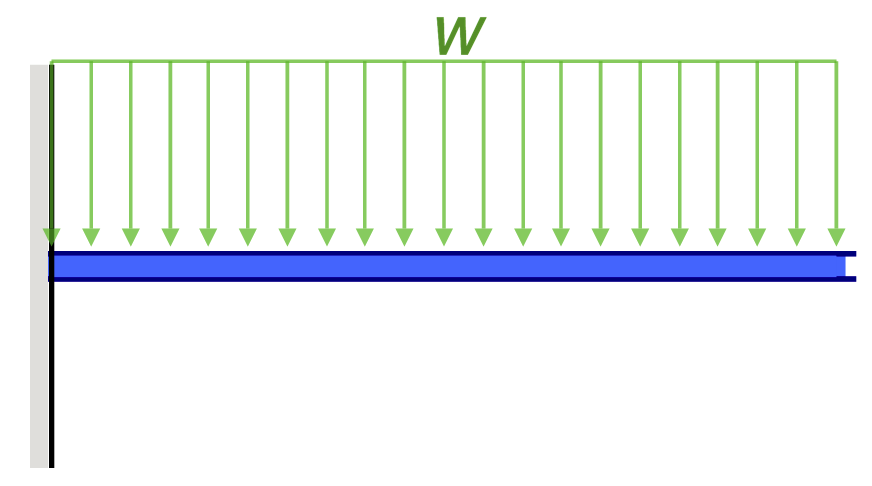
Er is een reeks vergelijkingen voor het berekenen van vrijdragende liggerkrachten en doorbuigingen. Deze kunnen worden vereenvoudigd tot een eenvoudige vrijdragende liggerformule, gebaseerd op het volgende::
Vrijdragende straalafbuigingen
Genomen uit onze formule en vergelijking van straalafbuiging pagina. Cantilever Beam-vergelijkingen kunnen worden berekend met de volgende formule, waar:
- W = belasting
- L = Lengte staaf
- E = Young's Modulus
- I = het traagheidsmoment van de straal
 |
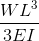 |
 |
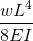 |
 |
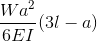 |
Cantilever Beam-momenten
Dus hoe berekenen we de maximale buigmomentkracht van een vrijdragende ligger? U kunt dit op dezelfde manier doen als in onze hoe het buigend moment in een balk te berekenen artikel. Echter, er zijn korte handvergelijkingen die u kunt gebruiken. Bijvoorbeeld, de vergelijking voor het buigend moment op elk punt x langs een vrijdragende balk wordt gegeven door:
\(M_x = -Px)
waar:
\(M_x \) = buigend moment in punt x
\(P. \) = belasting aangebracht aan het einde van de uitkraging
\(X \) = afstand vanaf het vaste uiteinde (steunpunt) naar een interessant punt langs de lengte van de straal.
Voor een verdeelde belasting, de vergelijking zou veranderen in:
\(M_x = – ∫wx) over de lengte (x1 tot x2)
waar: w = verdeelde belasting x1 en x2 zijn de integratiegrenzen.
Deze vergelijking is geldig voor een eenvoudige vrijdragende balk met een puntbelasting of een gelijkmatig verdeelde belasting op het vrije uiteinde van de balk. Er moet rekening mee worden gehouden dat vrijdragende liggers complexe belastings- en randvoorwaarden kunnen hebben, zoals meervoudige puntbelastingen, variërende verdeelde lasten, of zelfs schuine lasten, in die gevallen is de bovenstaande vergelijking mogelijk niet geldig, en een meer complexe aanpak kan nodig zijn, het is waar de FEA van pas komt.
Cantilever Beam Stress
Hoe spanning in een vrijdragende balk te berekenen? Cantilever Stress wordt berekend op basis van de buigkracht en is afhankelijk van de dwarsdoorsnede van de balk. Bijvoorbeeld, als een lid vrij klein is, er is niet veel dwarsdoorsnede waar de kracht zich over kan verspreiden, dus de stress zal behoorlijk hoog zijn. De belasting van de cantileverbalk kan worden berekend op basis van onze tutorial hoe de balkspanning te berekenen of gebruikend SkyCiv Balk Software – die de spanningen van uw balk zal laten zien.
Het is handig om op te merken dat vrijdragende balken meestal resulteren in spanning op de bovenste vezels van de balk. Dit betekent dat in het geval van een betonnen uitkragende ligger, primaire trekwapening is typisch vereist langs het bovenoppervlak. Dit in tegenstelling tot een conventionele betonnen balk die aan beide uiteinden wordt ondersteund, waar primaire trekwapening typisch aanwezig zou zijn langs het onderoppervlak van de balk.
Cantilever Beam-reactiekrachten
Uitkragingen buigen meer af dan de meeste soorten balken, omdat ze slechts vanaf één uiteinde worden ondersteund. Hierdoor is er minder steun voor de over te dragen last. Doorbuiging van de vrijdragende balk kan op een paar verschillende manieren worden berekend, inclusief het gebruik van vereenvoudigde vrijdragende liggervergelijkingen of vrijdragende liggerrekenmachines en software (meer informatie over beide vindt u hieronder). De vergelijking voor de reactie bij een vaste ondersteuning van een vrijdragende balk wordt eenvoudigweg gegeven door:
Reactiekracht in Y \( = R_y = P)
Momentkracht over Z \( = {F}_{j} = Px\)
waar:
\(F_y \) = reactiekracht in de Y-richting op steunpunt A (de vaste steun)
\(M_z \) = reactiemoment rond Z op steunpunt A (de vaste steun)
\(P. \) = de belasting aan het einde van de vrijdragende balk
\(X \) = afstand puntbelasting vanaf steunpunt
Deze vergelijking is van toepassing wanneer de belasting een puntbelasting op een uitkraging is. Wanneer de last is verdeeld, het is de som van alle krachten in verticale richting die nul moet zijn. De vergelijking wordt:
\(∑F_x = 0\)
Waarbij de reactiekracht de algebraïsche som zou zijn van alle verticale krachten die op de constructie werken. Deze vergelijking gaat ervan uit dat de ondersteuning een vaste ondersteuning is, wat betekent dat het geen rotatie of translatie heeft. Als de ondersteuning enkele vrijheidsgraden heeft, de vergelijking zou veranderen en complexer worden. Het is belangrijk om in gedachten te houden dat deze vergelijking slechts één stap is in het analyseren van een structuur, in het ontwerpproces van een echte constructie, verschillende overwegingen, zoals belastingscombinaties, veiligheidsfactoren, materiaaleigenschappen:, enzovoort. worden in aanmerking genomen alvorens een ontwerp te finaliseren.
Ontwerp met vrijdragende balk
Bij het ontwerpen van een vrijdragende constructie, verschillende belangrijke factoren moeten worden overwogen:
- Ladingen: De uitkraging moet de toegepaste belastingen kunnen dragen, inclusief het gewicht van de constructie zelf en eventuele extra belastingen zoals wind, sneeuw, en seismische belastingen. De belastingen moeten worden geanalyseerd en op de juiste manier over de constructie worden verdeeld.
- Kracht en stijfheid: De cantilever moet sterk en stijf genoeg zijn om doorbuiging te weerstaan, knikken, en andere soorten mislukkingen. De eigenschappen van de gebruikte materialen, zoals de elasticiteitsmodulus en de rekgrens, zal de sterkte en stijfheid van de structuur beïnvloeden.
- Spanningsconcentratie: Bij het ontwerp moet rekening worden gehouden met de spanningsconcentratie aan het vaste uiteinde van de uitkraging om falen te voorkomen. Spanningsconcentratie kan worden verminderd door grotere doorsneden te gebruiken of door afrondingen of afgeronde hoeken te gebruiken.
- Doorbuiging: De doorbuiging van de cantilever onder belasting moet worden geanalyseerd om ervoor te zorgen dat deze binnen aanvaardbare grenzen blijft, zowel om structurele veiligheid als om esthetische redenen.
- Duurzaamheid: De constructie moet ontworpen zijn om de beoogde levensduur te behouden met minimaal onderhoud. Hierbij wordt rekening gehouden met factoren als corrosie, vermoeidheid, en de effecten van verwering.
- Veiligheidsfactoren: Veiligheidsfactoren moeten in overweging worden genomen en in het ontwerp worden opgenomen om ervoor te zorgen dat de constructie bestand is tegen onverwachte belastingen of andere onvoorziene omstandigheden.
- Bouw methoden: Bij het ontwerp dient rekening te worden gehouden met de toe te passen constructiewijze, of het prefab is, ter plaatse gegoten, enzovoort. Dit heeft invloed op het type verbindingen en de algehele lay-out van de structuur.
- projecten duurden meestal een paar dagen/weken om ontwerpen om te draaien: Bij het ontwerp moet rekening worden gehouden met zowel de initiële kosten als de onderhoudskosten op de lange termijn.
- Bouwvoorschriften en voorschriften: Het ontwerp moet voldoen aan de relevante bouwvoorschriften en voorschriften in het rechtsgebied waar de constructie zal worden gebouwd. Bijvoorbeeld, als de balk van staal is en in de VS is gevestigd, het moet voldoen aan de vereisten van AISC 360 Ontwerpcontroles
Het is belangrijk om in gedachten te houden dat dit geen uitputtende lijst is, en de specifieke vereisten en overwegingen voor een vrijdragend ontwerp kunnen variëren, afhankelijk van de specifieke structuur en het beoogde gebruik. Een bouwkundig ingenieur met expertise in vrijdragend ontwerp zou met al deze factoren en meer rekening houden, om ervoor te zorgen dat het ontwerp veilig en effectief is.
Cantilever Beam-software
SkyCiv Balk Analyse Software stelt gebruikers in staat om vrijdragende balkconstructies eenvoudig en nauwkeurig te analyseren. U kunt een vereenvoudigde analyse van uw ligger krijgen, inclusief reacties, dwarskracht, buigmoment, doorbuiging, benadrukt, en onbepaalde stralen in een kwestie van seconden. Pas elke combinatie van belastingen toe en voltooi een volledig ontwerp volgens Amerikaan, Europese, Australisch, Canadese normen, om er een paar te noemen!
Als je het eerst wilt proberen, Gratis Online Balk Calculator een geweldige manier om te beginnen, of meld je vandaag nog gratis aan!


