Algemene beschrijving
SkyCiv heeft een robuuste en geavanceerde module voor het ontwerp van gewapende betonplaten. Om toegang te krijgen tot deze functie:, je moet eerst een model op SkyCiv S3D hebben gebouwd en vervolgens de module aanroepen voor automatische berekening met verschillende bouwcodes zoals ACI-318, Europese en Australische normen, enzovoorts. Het voornaamste doel van de module bij het plaatontwerp is het verschaffen van de hoeveelheid wapeningsstaven langs de plaat.
Figuur 1. SkyCiv plaatontwerpmodule
Als je nieuw bent bij SkyCiv, Meld u aan en test de software zelf!
SkyCiv-documentatie biedt uitstekende inhoud, inclusief voorbeelden en analysegevallen, zowel om te leren of u nieuw bent bij de modules, als om de resultaten van de plaatontwerpmodule te vergelijken met handmatige berekeningen. Bekijk gerust onze ontwerpvoorbeelden volgens ACI-318, Eurocode, en AS3600.
We raden u aan dit artikel te lezen voordat u complexe plaatsystemen diepgaand analyseert. Hier, je leert hoe de buigmomenten verschillen afhankelijk van de afmetingen van het plaatplan. Er zijn twee studiegevallen, eenrichtings- en tweerichtingsplaten. Dus, laten we beginnen met lezen!
Eenrichtings- versus tweerichtingsplaatgedrag
Laten we het plaatvoorbeeld in de volgende afbeelding bekijken, waarbij er steun is op elke plaatrand, en we stellen vast dat dit zich zal gedragen als een tweerichtingsplaat, dat is, met een buigmoment in de twee hoofdplanrichtingen.
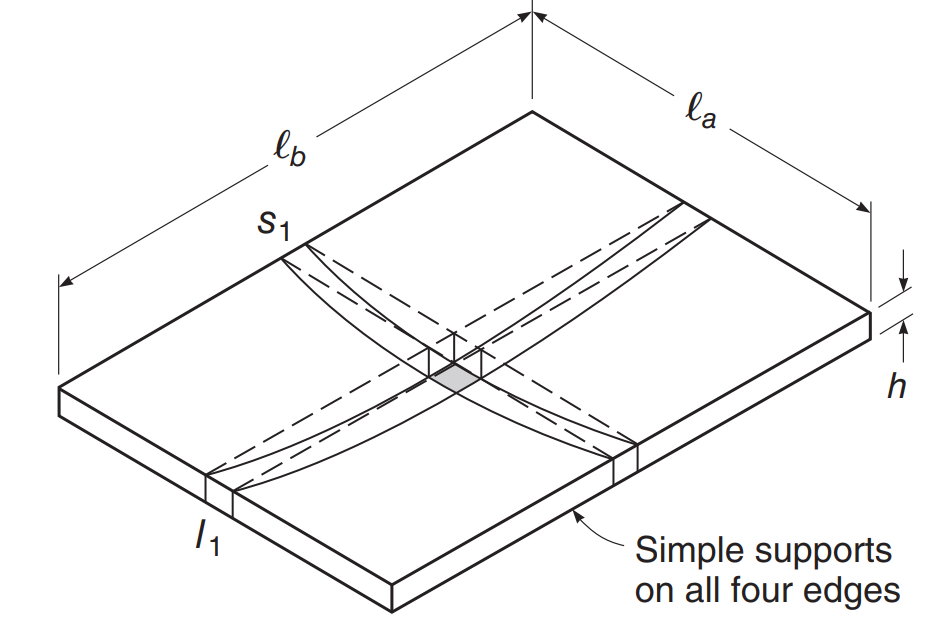
Figuur 2. Eenvoudig tweerichtingsplaatvoorbeeld over buigen. (David Darwin, Charles W.Dolan, Arthur H. Nilson, “Ontwerp van betonconstructies,” Vijftiende editie, McGraw-Hill-onderwijs)
We kunnen de verticale verplaatsing definiëren als (\(la < pond \)):
\(\Delta_a = \frac{{5}{w_a}{l_a^4}}{384{E}{I}}\)
\(\Delta_b = \frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
Omdat de plaat een doorlopend systeem is, beide verticale doorbuigingen zullen dezelfde waarde hebben. We kunnen de vergelijkingen vergelijken om een relatie uit te drukken tussen de belasting die door elke richting wordt gedragen als een functie van de planafmetingen.
\(\Delta_a = \Delta_b \to \frac{{5}{w_a}{l_a^4}}{384{E}{I}} = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
\(\frac{w_a}{w_b} = {(\frac{pond}{la}})^ 4 \)
Alle verwijzingen naar gewapend beton voor plaatontwerp zijn onderverdeeld in eenrichtings- en tweerichtingsverkeer als het quotiënt van \(\frac{pond}{la}\) groter of kleiner is dan een waarde van 2, respectievelijk.
Met behulp van de bovenstaande vergelijkingen, wanneer \(\frac{pond}{la}=2\), de belasting gedragen door de korte richting is gelijk aan \(w_a = {16}{w_b}\) en wanneer de waarde is \(\frac{pond}{la}=1), de belasting wordt gelijkmatig in beide richtingen verdeeld \(w_a ={w_b}\).
Eenrichtingsplaten momenten
Dus, we kunnen dat zien wanneer het quotiënt van dimensies groter is dan 2, praktisch, alle belastingen en buigmomenten zullen alleen in de korte richting geconcentreerd zijn. In dit geval is er sprake van eenrichtingsplaatgedrag, en het maximale buigmoment kan worden verkregen als een eenvoudig ondersteunde balk met een eenheidsbreedte.
\(M_{max,1,D}= frac{{w_a}{1 m}{l_a^2}}{8}\)
Tweerichtingsplatenmomenten
De oplossing van het geval van de tweerichtingsplaat is een complex en uitdagend probleem in de structurele mechanica. Je kunt in de onderstaande figuur zien dat de algemene analyse bestaat uit een plaat met volledige krachten en momenten in elke richting.
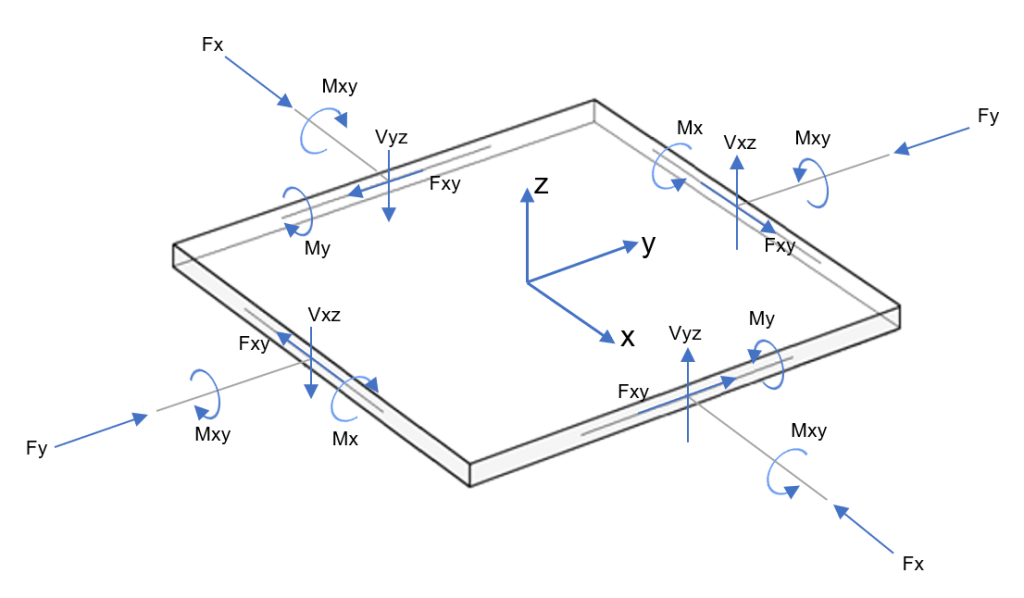
Figuur 3. Acties op plaatelement (buig- en torsiemomenten; normaal- en schuifkrachten)
Deze moeilijkheid komt voort uit het eigenlijke probleem dat moet worden opgelost: een partiële differentiaalvergelijking van de vierde orde waarbij buiging in twee richtingen nodig is. De vorm van deze vergelijking is:
\(\frac{\gedeeltelijk^4{w}}{{\gedeeltelijk}{x^4}} + {2}\frac{{\gedeeltelijk^4}{w}}{{{\gedeeltelijk}{x^2}}{{\gedeeltelijk}{j^2}}}+\frac{\gedeeltelijk^4{w}}{{\gedeeltelijk}{x^4}}-\frac{f_z}{D} = 0\)
Waar de plaatstijfheid (gebruikmakend van de elastische mechanische en geometrische eigenschappen) is \(D=\frac{{E}{t^3}}{{12}{(1-\nee^2)}}\).
De analytische oplossing van deze vergelijking is alleen beschikbaar voor eenvoudige ondersteuningsomstandigheden. De enige manier om een mogelijke oplossing te verkrijgen voor praktische en actuele gevallen is via numerieke methoden zoals de Eindige Elementenmethode.
SkyCiv gebruikt deze aanpak om plaatanalyse op te lossen. Op de volgende links, u krijgt toegang tot tutorials om meer te leren over de kenmerken van het SkyCiv-platform: Plaatontwerp in S3D en Hoe platen te modelleren? .
Als je nieuw bent bij SkyCiv, Meld u aan en test de software zelf!


