Definitie van frequentieanalyse?
Bij het ontwerpen van gebouwen, er zijn er twee soorten ladingen overwegen: statisch en dynamisch. Voor de eerste, het is alleen nodig om de directe respons van de constructie op de permanente belastingen in termen van verplaatsing en spanningen te berekenen. Dit kan worden bereikt met behulp van de stijfheid of de eindige-elementenmethode.
In het geval van dynamische analyse, het is een grotere uitdaging om rekening te houden met het bereik van mogelijke variaties in de reactie van de constructie als gevolg van tijdafhankelijke belastingen. Daarom, sommige nieuwe tools of functies worden essentieel om in de analyse op te nemen. Dus, frequentie analyse, een fundamentele methode in trillingsmechanica, ontstaat.
Deze methode verkrijgt de variatie in de tijd van de beweging van de constructie als gevolg van de uitgeoefende dynamische belastingen. Specifieker, dit houdt in dat de natuurlijke eigenschappen van trillingen van het structurele systeem worden gebruikt om interne krachten te berekenen, verplaatsingen, stabiliteitsproblemen, enzovoort.
Voor meer informatie over het onderwerp, we raden u aan een SkyCiv-artikel te lezen waarin in het kort wordt uitgelegd hoe u een Dynamische frequentieanalyse gebruik makend van SkyCiv-software voor structurele analyse.
Waarom is de frequentieanalyse relevant voor ontwerp??
De beste manier om het belang van frequentieanalyse in een ontwerp te meten, is kijken naar het geval van sommige structuren die zijn mislukt vanwege slecht dynamisch gedrag. Een beroemde brug in Noord-Amerika is de Tacoma Narrows, die uiteindelijk instortte na door de wind veroorzaakte aanhoudende periodieke trillingen. De volgende afbeeldingen tonen de grotere verplaatsing langs de brug net voor instorting, voornamelijk gericht op de rijbaan:

Figuur i. Laterale torsietrillingen in Tacoma Narrows Bridge

Figuur ii. Verhoogde verplaatsing op de brug vóór de ineenstorting.

Figuur iii. Catastrofale instorting van de brug
In deze casus, er is geen juiste frequentieanalyse uitgevoerd en de constructie was niet adequaat ontworpen om rekening te houden met de natuurlijke frequentie van de constructie.
eenvoudige slinger
De frequentieanalyse bestudeert de verschillende vormen die een structuur ontwikkelt wanneer deze wordt onderworpen aan externe dynamische acties. Dit is waarom je er verschillende krijgt modi. Gebruik dan deze formulieren, we kunnen de elementafmetingen van de structuur bepalen door de interne krachten die nodig zijn om het evenwicht te garanderen.
Voordat we dieper ingaan op technische en wiskundige overwegingen voor frequentieanalyse:, bekijk het volgende eenvoudige systeem van een slingerkolom getoond in figuur iv.
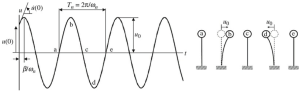
figuur iv. De dynamische respons van een vrij trillingspendulesysteem
Met behulp van een eenvoudige analyse zoals aangegeven in de laatste afbeelding, we kunnen elke keer de beweging van de topmassa voor de slingerkolom definiëren. Het belangrijkste doel van dit artikel is om de frequentieanalyse voor twee typische gevallen te behandelen:, enkele en meerdere vrijheidsgraden.
Enkele vrijheidsgraad
Dit specifieke geval is het eenvoudigst voor dynamische analyse. Het gedrag wordt beschreven met behulp van de evenwichtswet van D'Alembert, een uitbreiding van de tweede wet van Newton.
De volgende afbeelding toont de elementen van het SDOF-systeem:, stijfheid (k), demping (c), en massabron (m) voor traagheidskrachten. De in de tijd variërende externe kracht die op de massa wordt uitgeoefend, wordt weergegeven door \({p(t)}\).
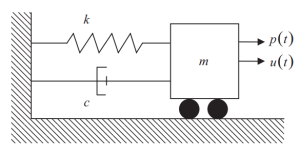
Figuur 1. Enkele vrijheidsgraad (SDOF) Systeem. (Schaal, 2017, pagina 56)
Alle elementen moeten voldoen aan de dynamische evenwichtsvoorwaarde:
\({m}{\punt{u}}+{c}{\punt{u}}+{k}{u}={p(t)}\)
Dit is een lineaire differentiaalvergelijking van de tweede orde, en de oplossing ervan heeft twee componenten::
\({u(t)}={u}_{h}(t)+{u}_{p}(t)\)
Waarbij:
- \({u(t)}\) is de absolute verplaatsing.
- \({u}_{h}(t)\) is de homogene oplossing, over het algemeen met betrekking tot het geval van gratis trillingen;.
- \({u}_{p}(t)\) is de specifieke oplossing volgens de toegepaste excitatie?.
We zullen ons alleen concentreren op de homogene oplossing om trillingsgedrag te beschrijven en de meest kritische dynamische kenmerken die een structuur heeft.
Laten we de volgende termen definiëren::
\({\zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt{n}}={\sqrt(\frac {k}{m})}\) Hoekfrequentie
\({\xi}={\frac{c}{{2}{m}{\omega_n}}}={\frac{c}{{2}{\sqrt(\frac {k}{m})}}}\) Fractie van kritische demping
Wanneer de fractie kritische demping kleiner is dan 1, de trillingskast wordt ondergedempt; dat is, er zullen voltooide cycli zijn voordat de beweging stopt.
De oplossing heeft de volgende algemene vorm:
\({u_h}={e^{{-\xi}{\zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt{n}}{t}}}{[{A}{omdat}{\omega_d}{t}+{B}{zonder}{\omega_d}{t}]}\)
Waarbij:
- A en B zijn integratieconstanten die afhankelijk zijn van de beginvoorwaarden van beweging.
- \({\omega_d}={\omega_n}{\sqrt({{1}-{\xi^2}})}\) is de gedempte hoekfrequentie
Na evaluatie van A- en B-constanten, de algemene oplossing voor de ongedempte behuizing is:
\({u_h}={e^{{-\xi}{\zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt{n}}{t}}}{[{u_0}{omdat}{\omega_d}{t}+{\frac{{\punt{u_0}}+{\xi}{\omega_n}{u_0}}{\omega_d}}{zonder}{\omega_d}{t}]}\)
Waarbij:
- \({u_0}\) is de initiële massaverplaatsing
- \(\punt{u_0}\) is de beginsnelheid van de massa
Als we de oplossing plotten met enkele waarden van beginvoorwaarden, we zullen de volgende figuur verkrijgen:.
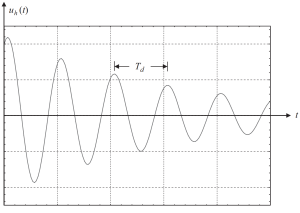
Figuur 2. Verplaatsing resulteert in een homogeen deel van de oplossing in een subkritisch gedempt geval. (Schaal, 2017, pagina 58)
In het andere geval, het is cruciaal om te analyseren wat er gebeurt als de fractie kritische demping een waarde heeft van 1. \({\xi}=1). Deze toestand impliceert een structuur met volledige demping.
De te gebruiken vergelijking is
\({u_h}={e^{{-\zodat ingenieurs precies kunnen nagaan hoe deze berekeningen zijn gemaakt{n}}{t}}}{\{u_0+({\punt{u_0}}+{\omega_n}{u_0}){t}}\}\)
En hun grafiek met verschillende gevallen van beginvoorwaarden staat in de volgende afbeelding:.
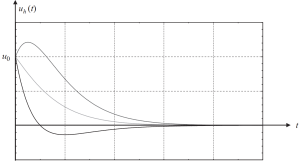
Figuur 3. Verplaatsing resulteert in een homogeen deel van de oplossing in een kritisch gedempte behuizing. (Schaal, 2017, pagina 58)
Responsparameters
De vorige sectie heeft ons geholpen om de oplossing voor gratis dynamische trillingen in een SDOF-systeem te definiëren. De twee belangrijkste parameters zijn natuurlijke frequentie \(\omega_n\) die aangeeft hoe de structuur uit zichzelf zal trillen, en de fractie kritische demping \(\xi), die de snelheid definieert in afnemende trillingen.
Over het algemeen, constructies hebben een lage demping met een maximale waarde van \(\xi)=10 %. Als we de gedempte eigenfrequentie evalueren met behulp van deze waarde, het resultaat is \({\omega_d}= 0,995{\omega_n}\). Dus, het wordt aanbevolen om te gebruiken \({\omega_d}{\dikongeveer}{\omega_n}\).
We kunnen de dynamische eigenschappen samenvatten in de volgende tabel:.
| Hoekfrequentie (rad/s) | Natuurlijke frequentie (Hz) | Natuurlijke periode (s) | |
|---|---|---|---|
| Hoekfrequentie \({\omega_n}\) | \({\omega_n}\) | \(2{\pi}{f_n}\) | \(\frac{2{\pi}}{T_n}\) |
| Natuurlijke frequentie \({f_n}\) | \(\frac{\omega_n}{2{\pi}}\) | \(f_n\) | \(\frac{1}{T_n}\) |
| Natuurlijke periode \({T_n}\) | \(\frac{2{\pi}}{\omega_n}\) | \(\frac{1}{f_n}\) | \(T_n\) |
Tafel 1. Relatie tussen hoekfrequentie, natuurlijke frequentie, en periode (Schaal, 2017, pagina 60)
Meerdere vrijheidsgraden
Wanneer er veel massa's in een structuur bestaan, we moeten meerdere coördinaten definiëren om de positie op elk moment voor deze massa's te beschrijven. Een specifiek en voor de hand liggend voorbeeld wordt getoond in de volgende afbeelding:, bestaande uit een complexe slinger waarbij verschillende hoeken nodig zijn om de positie op elk bewegingsmoment vast te stellen.
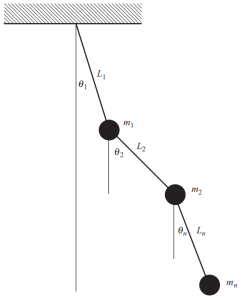
Figuur 4. Pendel met meerdere massa's. (Schaal, 2017, pagina 53)
In deze sectie, we analyseren structuren’ algemene dynamische respons met behulp van de uitbreiding van eigenschappen frequentieanalyse voor meerdere vrijheidsgraden.
Het is absoluut noodzakelijk om op de hoogte te zijn van het modelleringsproces bij het omgaan met een daadwerkelijke structuur. De volgende afbeeldingen beschrijven de vereiste stappen om een wiskundig model te construeren dat klaar is om de frequentieanalyse toe te passen om de dynamische respons te beschrijven.
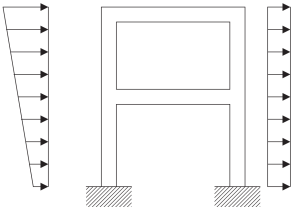
Figuur 5. Fysiek model van een continuüm structureel frame. (Schaal, 2017, pagina 23)
De eerste stap omvat het samenvoegen van massa's op elk niveau van kruising van liggers en kolommen. Elke knoop heeft drie mogelijke bewegingen, twee lineaire verplaatsingen, en één omwenteling. Consistent zijn in de analyse, massa's en polaire traagheidseigenschappen moeten worden overwogen.
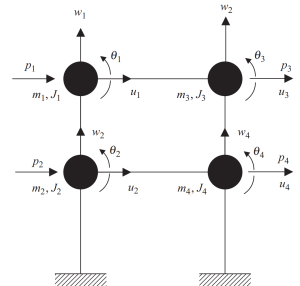
Figuur 6. Samengeklonterde massa's op knooppunten met verplaatsings- en rotatievrijheidsgraden. Discreet systeem. (Schaal, 2017, pagina 23)
De statische condensatiemethode kan de complexiteit van de analyse helpen verminderen, verwaarlozing van rotatie- en translatietraagheid.
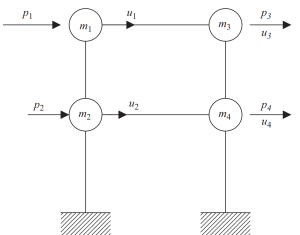
Figuur 7. Statische condensatie van de vrijheidsgraad tot alleen horizontale verplaatsing. (Schaal, 2017, pagina 23)
In de laatste stap, we kunnen de horizontale beweging voor dit framevoorbeeld in slechts twee knooppunten samenvoegen.
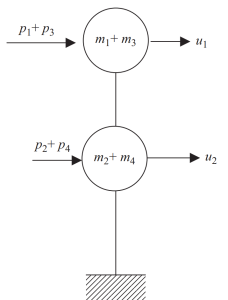
Figuur 8. Uiteindelijke statische condensatie naar twee knooppunten en vrijheidsgraad van horizontale verplaatsing. (Schaal, 2017, pagina 24)
Zoals we in de vorige sectie deden met het SDOF-systeem, we zullen de oplossing voor de bewegingsvergelijking voor meerdere vrijheidsgraden ontwikkelen.
De bewegingsvergelijking schrijft in matrixvorm als
\([M]\{\punt{u}\} + [C]\{\punt{u}\}+[K]\{jij}={p(t)}\)
Waarbij:
- \([M]\) is de massamatrix
- \([C]\) is de dempingsmatrix van Coulumb
- \([K]\) is de stijfheidsmatrix
We moeten de gratis trillingsoplossing bestuderen om de responsparameters te verkrijgen. Er wordt geen demping en kracht op het systeem uitgeoefend, alleen de beginvoorwaarden die moeten worden geëvalueerd.
\([M]\{\punt{u}\} +[K]\{jij}={0}\)
Naar analogie van het eerste geval voor een SDOF, we kunnen een sinusoïdale oplossing van de vorm testen.
\({u(t)}={\phi}{({een}{omdat}{\omega}{t}+{b}{zonder}{\omega}{t})}\)
\({\punt{u}{(t)}}={-{\omega}^ 2}{\phi}{({een}{omdat}{\omega}{t}+{b}{zonder}{\omega}{t})}\)
waarin de vector \(\phi) is een vormvector die niet tijdsafhankelijk is. de coëfficiënten “een” en “b” zijn constanten die worden verkregen bij het evalueren van beginvoorwaarden.
Na vervanging van beide uitdrukkingen voor de testoplossing in de bewegingsvergelijking, we verkrijgen het lineaire eigenwaarde-eigenvectorprobleem:
\([K]{\phi}={{\omega}^ 2}[M]{\phi}\)
Waarbij:
- \({{\omega}^ 2}\) is de verzameling eigenwaarden
- \({\phi}\) is de verzameling eigenvectoren
De oplossing voor dit klassieke probleem voor het framevoorbeeld in de nieuwste cijfers laat zien hoe massa's zullen trillen. Dit betekent dat elke massa in horizontale richting zal bewegen volgens de waarde van eigenvectoren.
Kijk naar de volgende afbeelding van dit gedrag:.
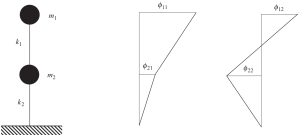
Afbeelding nr. 9. Frequentieanalyse die de resultaten van de twee eigenvectoren toont. (Schaal, 2017, Bladzijde 135)
SkyCiv Structural 3D
Voer frequentieanalyses uit voor uw constructies met SkyCiv Structural 3D. Meld u vandaag nog aan om te beginnen!
Referenties:
- Eduardo Kausel, (2017). “Geavanceerde structurele dynamiek” 1e editie, Cambridge University Press


