Een gids voor statische bepaling, onbepaaldheid, en instabiliteit
Zodra de constructie volledig is gemodelleerd en de belastingen zijn aangebracht, het is tijd om het systeem op te lossen om alle resultaten te vinden die uit de analysefase komen: reacties, Interne krachten (dwarskracht, buigmoment, axiale kracht, en torsie), verplaatsingen, en benadrukt. Soms gaan dingen niet zoals verwacht en als het om het oplossen gaat, Het kan zijn dat u een vervelende melding krijgt “Oplossen mislukt! Controleer uw structuuropstelling, omdat het model waarschijnlijk instabiel is”, en de kans is groot dat je niet precies weet wat er mis is met het model. In dit artikel wordt het concept van structurele stabiliteit uitgelegd, samen met statische bepaaldheid en onbepaaldheid, die zeer verwante onderwerpen zijn, het bevat ook enkele tips voor het oplossen van problemen met een onstabiel model.
Over het algemeen, Een constructie wordt als intern stabiel beschouwd als deze zijn vorm behoudt wanneer de steunen worden verwijderd. Omgekeerd, een constructie wordt als intern onstabiel beschouwd als deze eenmaal is losgemaakt van de steunen, de constructie kan zijn vorm niet behouden en kan grote verplaatsingen ondergaan of zelfs instorten. Dat gezegd hebbende, we zullen de statische bepalingsformule nader bekijken, zowel voor intern onstabiele als stabiele constructies. De statische bepalingsformule helpt een structuur als extern onstabiel te classificeren, statisch bepaald, of statisch onbepaald.
Statische bepaling van intern stabiele structuren
Een intern stabiele structuur kan extern als statisch bepaald worden beschouwd als al zijn steunreacties kunnen worden opgelost door de evenwichtsvergelijkingen op te lossen. Voor vlakke constructies onder belasting in het vlak, Er zijn drie ondersteunende reacties nodig om de structuur in evenwicht te brengen. Bovendien, aangezien er slechts drie evenwichtsvergelijkingen beschikbaar zijn, Er zijn maximaal drie reacties te vinden, er zouden dus precies drie reacties moeten zijn die de vlakstructuur ondersteunen. Enkele voorbeelden van extern statisch bepaalde vlakke structuren worden in de volgende afbeelding getoond:
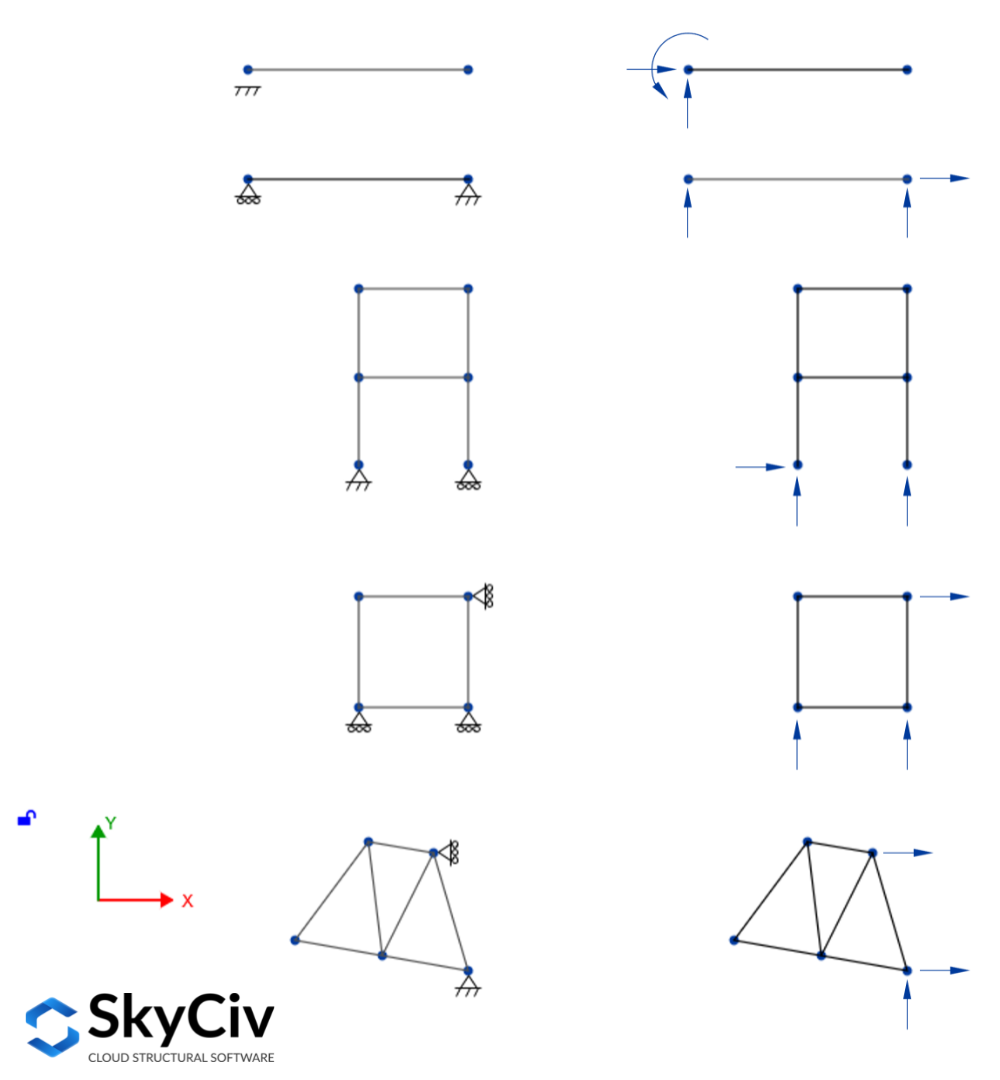
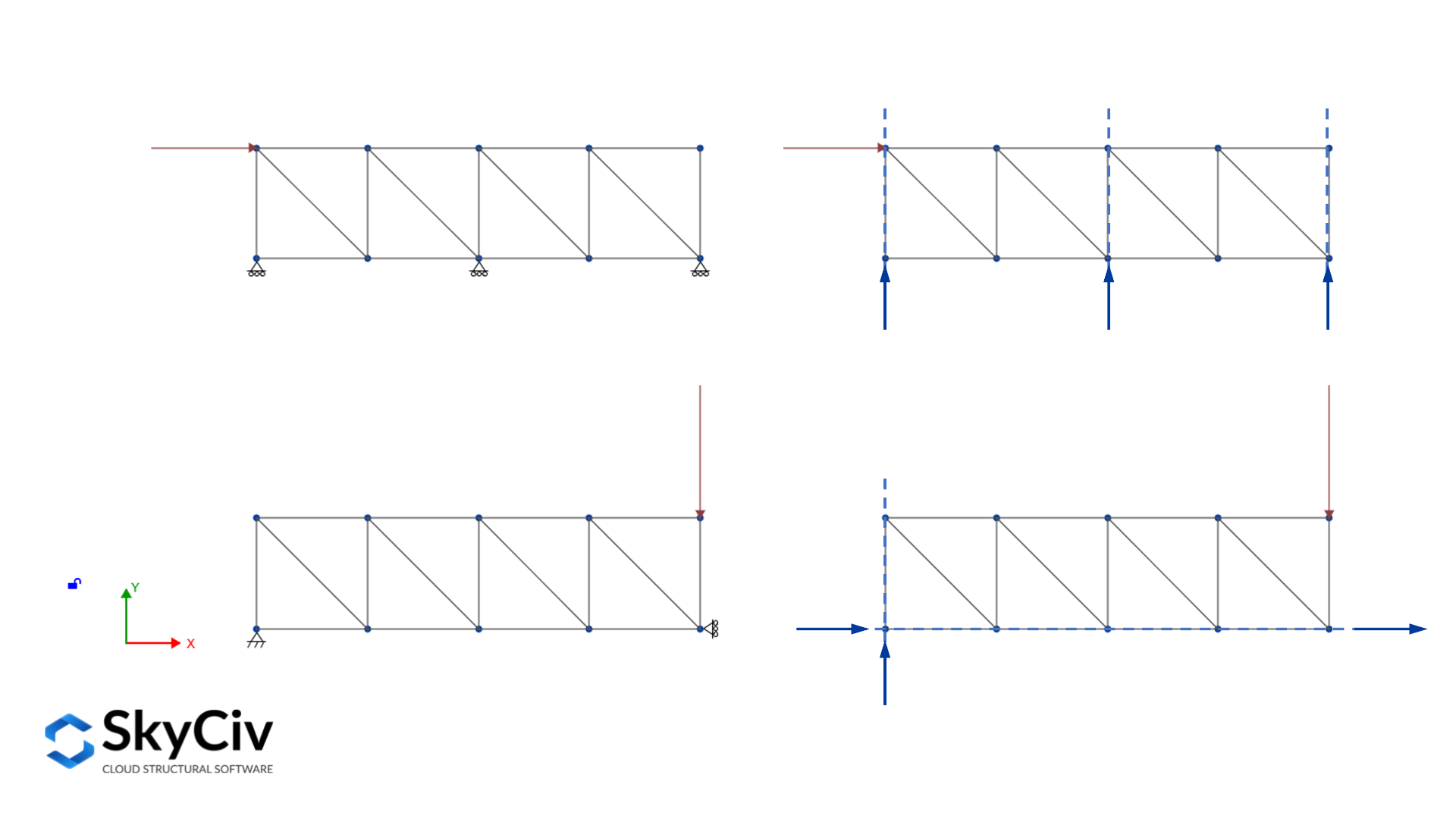
Wanneer meer dan drie reacties de structuur ondersteunen, het wordt een statisch onbepaalde externe structuur genoemd, omdat het niet mogelijk is om alle reacties op te lossen met behulp van de drie evenwichtsvergelijkingen. Deze reacties worden extern redundant genoemd en het aantal extern redundante reacties staat bekend als de mate van externe onbepaaldheid, geschreven als een vergelijking ziet het er zo uit:
\(ik_e = r – 3\)
Waarbij \(R) is het aantal reacties dat de structuur ondersteunt.
In de gevallen dat de constructie wordt ondersteund door minder dan drie steunreacties, die zijn niet genoeg om te voorkomen dat de constructie in zijn vlak beweegt, aangezien die structuur onder een algemeen systeem van belastingen niet in evenwicht zou blijven, wordt het extern statisch onstabiel genoemd. Op basis van het aantal reacties \(R), het is mogelijk om de statische bepaaldheid te bepalen, onbepaaldheid, en instabiliteit van intern stabiele structuren met behulp van de volgende criteria:
\( r begin{° en 60°} < 3, \; \tekstrm{statisch onstabiele externe structuur} \\ = 3, \; \tekstrm{statisch bepaalde externe structuur} \\ > 3, \; \tekstrm{statisch onbepaalde externe structuur} \einde{° en 60°}\)
Het is belangrijk om te vermelden dat zodra aan de laatste twee voorwaarden is voldaan, het is niet zeker dat de structuur stabiel zal zijn. Het betekent dat zelfs wanneer de constructie wordt ondersteund door meer dan drie reacties als de ondersteuningen niet goed zijn gerangschikt, de constructie nog steeds instabiel kan zijn. Dit wordt geometrische externe instabiliteit genoemd en wordt veroorzaakt door twee belangrijke redenen:
- Wanneer alle reacties’ De werkingslijnen zijn parallel omdat niet wordt verhinderd dat de structuur zich in de loodrechte richting van de reacties verplaatst
- Wanneer alle reacties’ actielijnen zijn op één punt gelijktijdig omdat de structuur rond het gelijktijdigheidspunt kan roteren
Statische bepaling van intern onstabiele structuren
Intern onstabiele constructies zijn constructies die, wanneer ze loskomen van de steunen, hun oorspronkelijke vorm niet kunnen behouden. Zonder steunen, de leden van de constructie zouden grote verplaatsingen ten opzichte van elkaar ondergaan. Om de statische bepaling te definiëren, onbepaaldheid, en externe stabiliteit van deze structuren, de vergelijkingen veranderen als gevolg van de aanvullende toestandsvergelijkingen die een rol spelen en rekening houden met de speciale verbindingen tussen leden. De speciale verbindingen zijn verbindingen die geen moment overbrengen, dwarskracht, of axiale kracht.
Als voorbeeld, bekijk de structuur in de onderstaande afbeelding (bovenste gedeelte), het wordt duidelijk ondersteund door drie reacties, maar deze zijn niet voldoende om het evenwicht te garanderen onder de uitgeoefende krachten in het vlak dankzij de aanwezigheid van het scharnier tussen de leden, het heeft een vierde niet-parallel nodig, niet-gelijktijdige reactie om evenwicht te garanderen (onderste gedeelte).
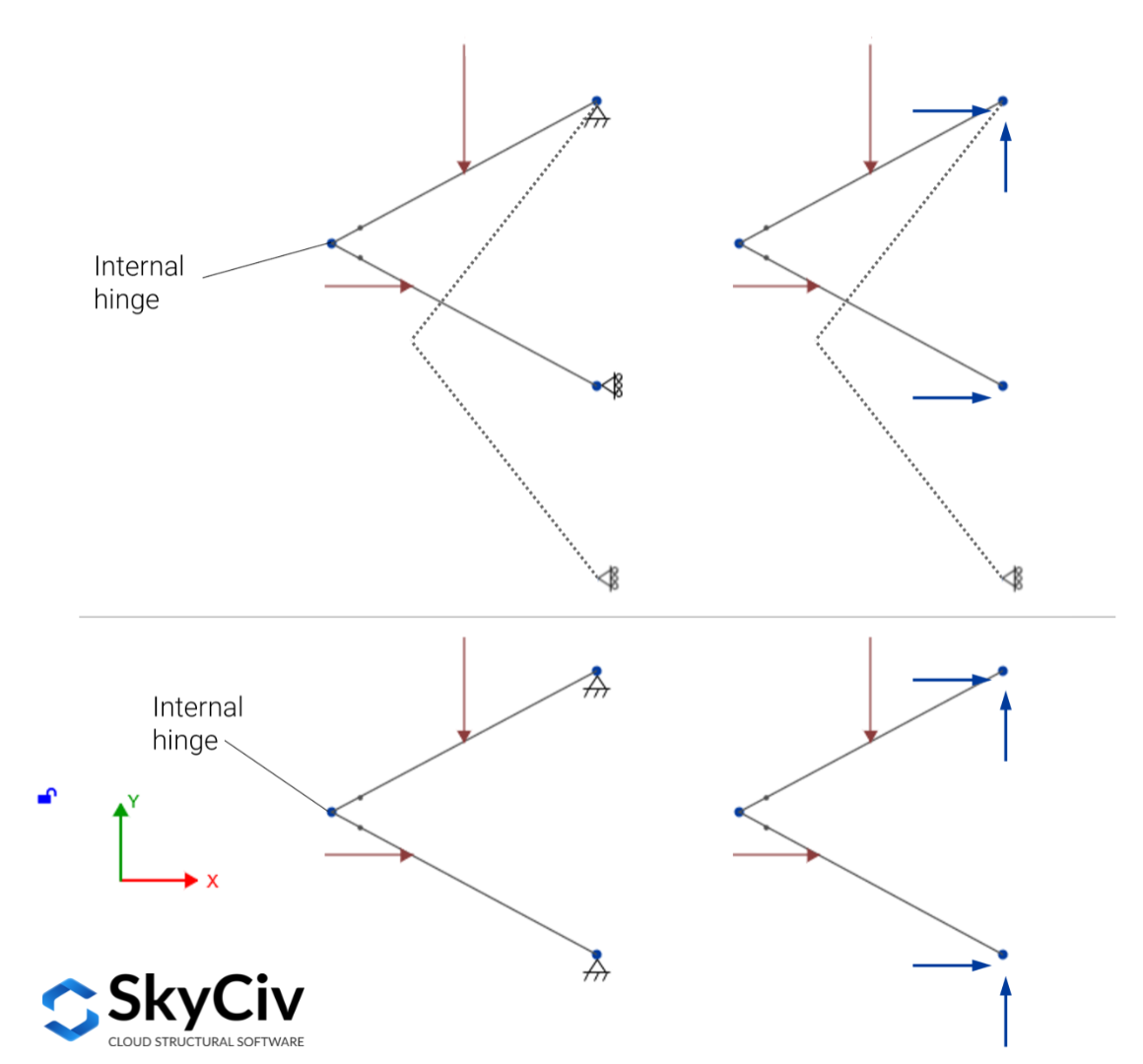
Over het algemeen, voor intern onstabiele constructies, op basis van het aantal reacties \(R) en toestandsvergelijkingen \(e_c), het is mogelijk om de statische bepaaldheid te bepalen, onbepaaldheid, en instabiliteit van intern stabiele structuren met behulp van de volgende criteria:
\( r begin{° en 60°} < 3 + e_c, \; \tekstrm{statisch onstabiele externe structuur} \\ = 3 + e_c, \; \tekstrm{statisch bepaalde externe structuur} \\ > 3 + e_c, \; \tekstrm{statisch onbepaalde externe structuur} \einde{° en 60°}\)
Voor onbepaalde extern intern onstabiele constructies, de mate van externe onbepaaldheid kan als volgt worden uitgedrukt:
\(ik_e = r – (3 + e_c)\)
Afronden
Voor vlakke structuren die intern stabiel zijn, om extern stabiel te zijn, wat betekent dat het in evenwicht blijft onder een algemeen systeem van belastingen, het volgende moet gelden:
- De structuur wordt ondersteund door drie of meer reacties
- Alle reacties kunnen niet parallel of gelijktijdig zijn
Om vlakke constructies die intern onstabiel zijn, extern stabiel te maken, wat betekent dat het in evenwicht blijft onder een algemeen systeem van belastingen, het volgende moet gelden:
- Het aantal reacties dat de structuur ondersteunt is groter dan of gelijk aan het aantal toestandsvergelijkingen plus drie
- Alle reacties kunnen niet parallel of gelijktijdig zijn
Problemen oplossen met een onstabiele structuur in S3D
Er zijn een paar dingen die u kunt proberen als het model niet oplost, en je krijgt de “Instabiele structuur” foutmelding:
- Selecteer alle leden en zorg ervoor dat ze hun eindfixaties voor leden hebben “FFFFFF”, en probeer het model uit te voeren. Als sommige leden een andere eindvastheid in het uiteindelijke model nodig hebben, begin deze één voor één te veranderen en los de structuur op om te zien welk lid of welke reeks leden precies de instabiliteit veroorzaakt.
- Selecteer alle leden en wijzig hun type van normaal naar continu, die op de juiste manier leden zou verbinden die geen knooppunt in de kruising hebben, maar die bedoeld zijn om te worden verbonden.
- Verwijder alle kabels uit de analyse, en probeer het model op te lossen. Om te leren hoe je leden kunt onderdrukken, verwijzen naar Dit artikel.
Referenties
Kassimali, Aslam. “3.4 Statische bepaling, onbepaaldheid, en instabiliteit.” Structurele analyse, Cengage leren, 2011.


