ORTHOTROPISCHE MATERIALEN
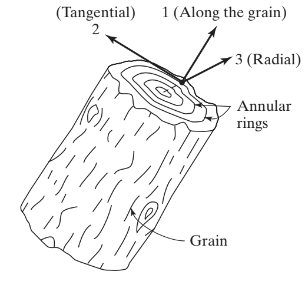
Voordat we een uitleg over orthotrope platen doornemen, laten we eens kijken naar enkele voorbeelden van orthotrope materialen. Materialen zoals kristallen van topaas en bariet zijn orthotroop (Chandrupatla, 2012). Een ander veelgebruikt orthotroop materiaal is hout. Figuur 1 toont de belangrijkste assen waarin mechanische eigenschappen voor hout zijn gedefinieerd.
Figuur 1. Hout als orthotroop materiaal (Chandrupatla & Belegundu ,2012, pagina 233)
as 1 wordt gedefinieerd langs de korrel of vezels; as 2 is tangentieel en as 3 loopt radiaal. De gegeneraliseerde wet van Hooke voor dit voorbeeld (en voor elk ander orthotroop materiaal) kan worden geschreven als
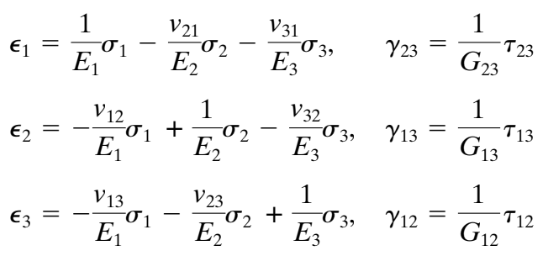
Vergelijkingen 1. Gegeneraliseerde wet van Hooke (Chandrupatla & Belegundu,2012, pagina 233)
Waarbij:
- e1, e2, e3 zijn de normale spanningen.
- c12, c13, c23 zijn de schuifspanningen.
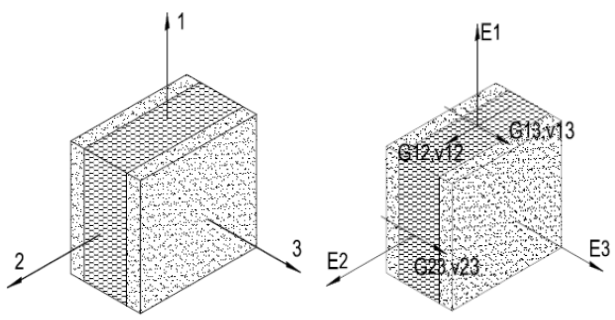
- E1, E2, en E3 zijn de Young's modulus langs de hoofdas.
- G12, G13, G23 zijn de afschuifmodulus.
- n21, n31, n12, n32, n23 zijn de verhoudingen van Poisson.
- Voor gecombineerde indexen, het eerste cijfer geeft aan waar spanning wordt uitgeoefend en het tweede waar vervorming optreedt.
Daarom, het belangrijkste verschil in een orthotroop materiaal is dat we verschillende mechanische eigenschappen hebben langs de hoofdassen, dat is, “X”, “j”, “z”.
ORTHOTROPISCHE PLATEN
Er zijn enkele veelvoorkomende use-cases voor borden bij bouwtechniek, dat we als volgt kunnen samenvatten:: isotroop vlak, composiet of sandwich en verstijfd (W. Jiang et al, 1997).
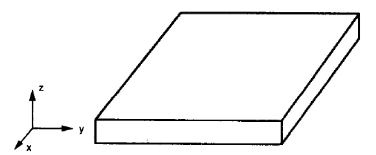
Isotrope vlakke platen zijn gewone platen (figuur nr.2), het is alleen nodig om één waarde voor de Poisson-ratio te definiëren, Jong, en afschuifmodulus omdat de mechanische eigenschappen in geen enkele richting veranderen.
Figuur nr.2. Vlakke platen zijn gewoonlijk isotroop (W. Jiang et al, 1997, pagina 106)
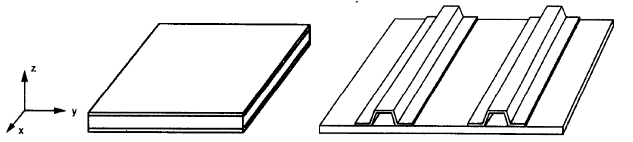
Voor de twee laatste opties, sandwich en verstijfde platen (figuur nr.3), we moeten verschillende mechanische eigenschappen in hun hoofdas definiëren. Deze verschillende waarden maken platen orthotroop.
Figuur 3. Composiet (links) en hoedenverstevigde platen (Rechtsaf) (W. Jiang et al, 1997, pagina 106)
In een orthotrope plaat, we zouden twee assen hebben met dezelfde stijfheid, figuur nr.3. Assen "x" en "y" liggen op een vlak, en "z" staat er loodrecht op.
We kunnen stellen dat (W. Jiang et al, 1997):
- EX = Ej ≠ Ez ; (EX, Ej )> Ez .
- nxz = neeyz neexy ; (nxz, nyz) >nxy
- Gxy = Gxz = Gyz
De eerder aangegeven uitdrukkingen houden in dat de stijfheid in de "x"- en "y"-richtingen hoger is dan "z". De verhoudingen van Poisson laten ook zien dat er meer vervorming is in vlakken die verband houden met de "z"-richting dan in een vlak gevormd door de "x"- en "y"-as.
VOORBEELD
Beschrijving en instellingen
Om de concepten die in eerdere secties zijn geleerd samen te vatten:, we gaan een voorbeeld ontwikkelen in SkyCiv. Het bestaat uit de analyse van een sandwichwand/plaatpaneel dat is opgebouwd uit twee spuitbetonlagen gescheiden door een polystyreenkern. We hebben de volgende referentie gekozen voor de mechanische eigenschappen die bij het modelleren moeten worden gebruikt:: Torres Villavicencio et al. (2013).

Figuur 4. Sandwichwand/plaatpaneel
Om het verschil in analyse in platen vast te leggen wanneer we de geavanceerde opties selecteren (orthotroop), we ontwikkelen een korte vergelijking van de hierboven beschreven panelensandwich en een benadering van hun mechanische eigenschappen met behulp van een isotrope benadering. Het laatste geval gebruikt waarden in mechanische eigenschappen die niet veranderen langs hun hoofdassen.
Het doel van dit voorbeeld is om de resultaten te vergelijken in termen van verticale verplaatsing. De modelopstelling wordt getoond in Figuur 5.
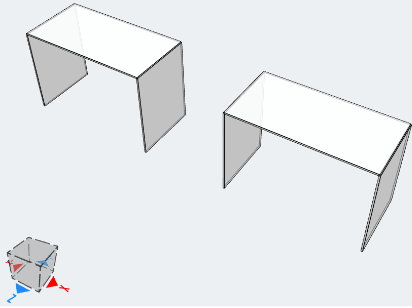 Figuur 5. Modelopstelling. Orthotroop (links), isotroop (Rechtsaf)
Figuur 5. Modelopstelling. Orthotroop (links), isotroop (Rechtsaf)
Mechanische eigenschappen
Gebaseerd op verschillende laboratoriumtestrapporten, de orthotrope eigenschappen van het paneel zijn: (Torres Villavicencio et al, 2013):
| Eigendom | Waarde |
|---|---|
| E1 (MPa) | 5613 |
| E2 (MPa) | 5613 |
| E3 (MPa) | 2807 |
| G12 (MPa) | 2245 |
| G23 (MPa) | 1123 |
| G13 (MPa) | 1123 |
| n12 | 0.2 |
| n23 | 0.25 |
| n13 | 0.25 |
Tabel nr.1. Sandwichpaneel orthotrope mechanische eigenschappen
Figuur nr.6. Hoofdassen in paneelelement (Torres Villavicencio et al, 2013).
De benadering voor het isotrope geval wordt aangegeven in de onderstaande tabel:.
| Eigendom | Waarde |
|---|---|
| E (MPa) | 5613 |
| G (MPa) | 2245 |
| n | 0.20 |
Tabel nr.2. Sandwichpaneel Isotrope Mechanische Eigenschappen Benadering
Modelleren in SkyCiv
We beschrijven nu op een zeer beknopte manier de stappen die nodig zijn om het voorbeeld te modelleren. (Voor meer details over het modelleren van platen, raadpleeg deze link SkyCiv-plaatmodellering). Ik heb SkyCiv niet geprobeerd, volg mee met Structural 3D, eenvoudig meld je hier gratis aan.
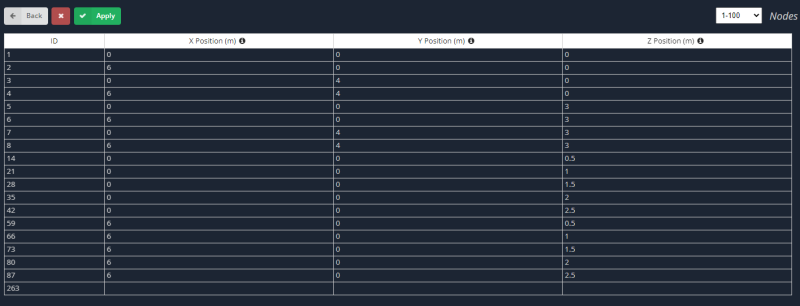
- Knooppunten: Beide gevallen maken, we definiëren eerst de knooppunten die overeenkomen met de horizontale en verticale platen.

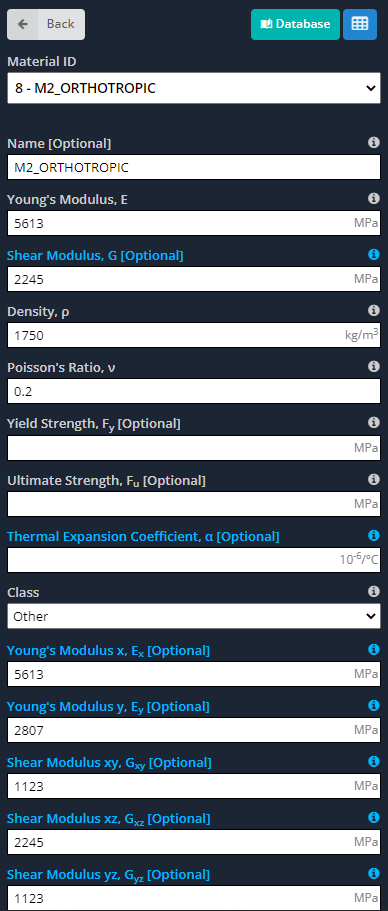
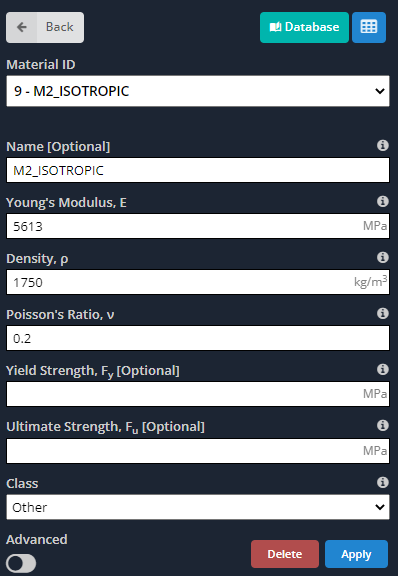
- Materialen: Zoals we al eerder zeiden, orthotrope materialen hebben verschillende eigenschappen langs hun hoofdassen. De volgende afbeeldingen geven de invoer aan die we voor het model moeten definiëren.


- Borden: Via modelknooppunten creëren we de rechthoekige platen. Twee voor de verticale wandmodellering en één voor de vloer of plaat.

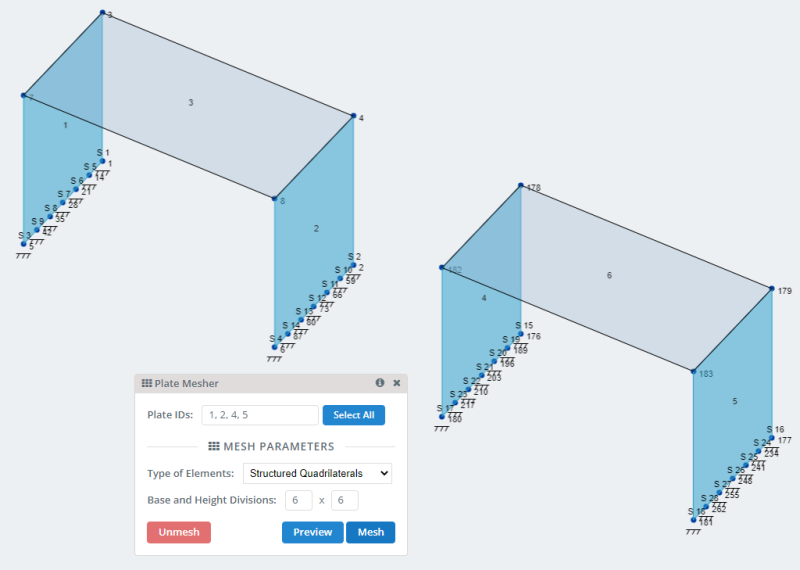
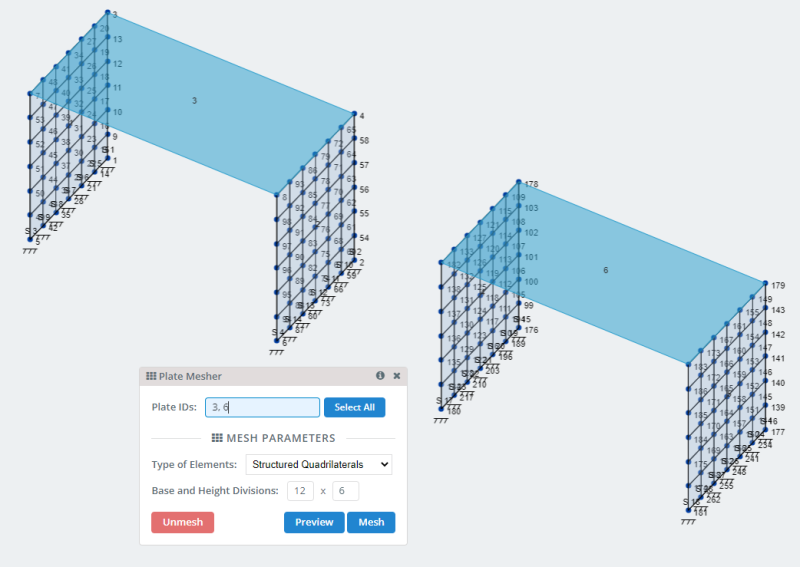
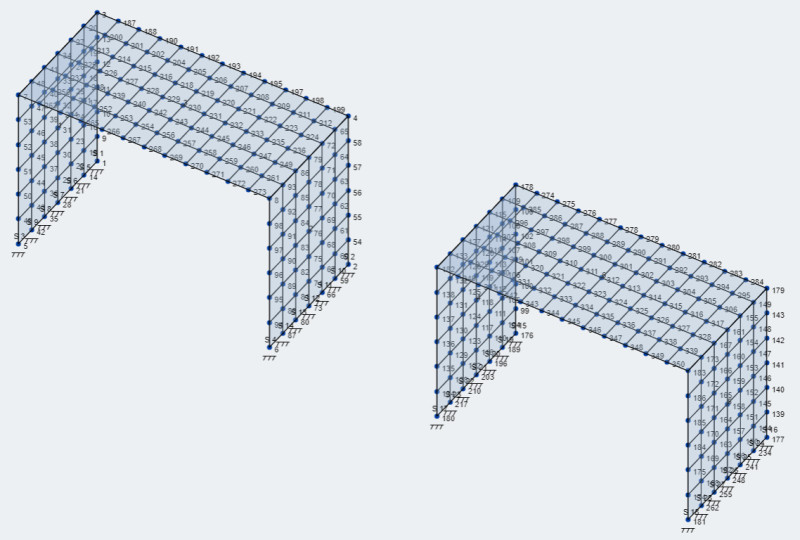
- Gaasplaten: SkyCiv heeft veel opties om platen te meshen en kan worden geraadpleegd in Je bord roosteren . Laten we voor ons model de optie van gestructureerde vierhoeken gebruiken.



- Belastinggeval met eigen gewicht definiëren: We beschouwen deze eigengewichtsbelasting alleen om het algemene structurele gedrag van de plaat vast te leggen.

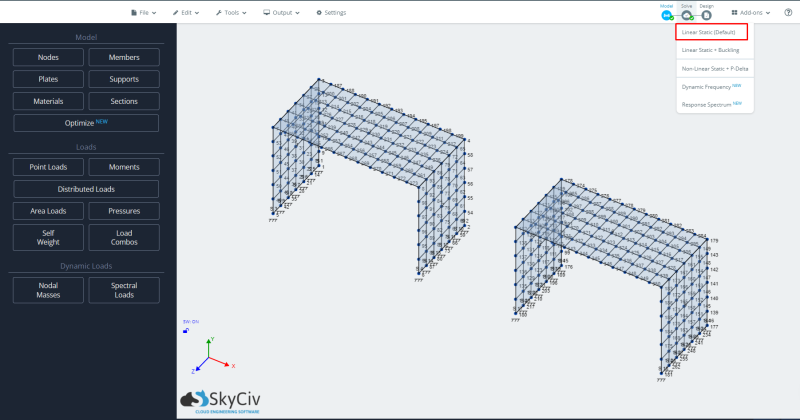
- Analyse uitvoeren: Om het model uit te voeren, selecteren we het lineaire statische analysegeval.

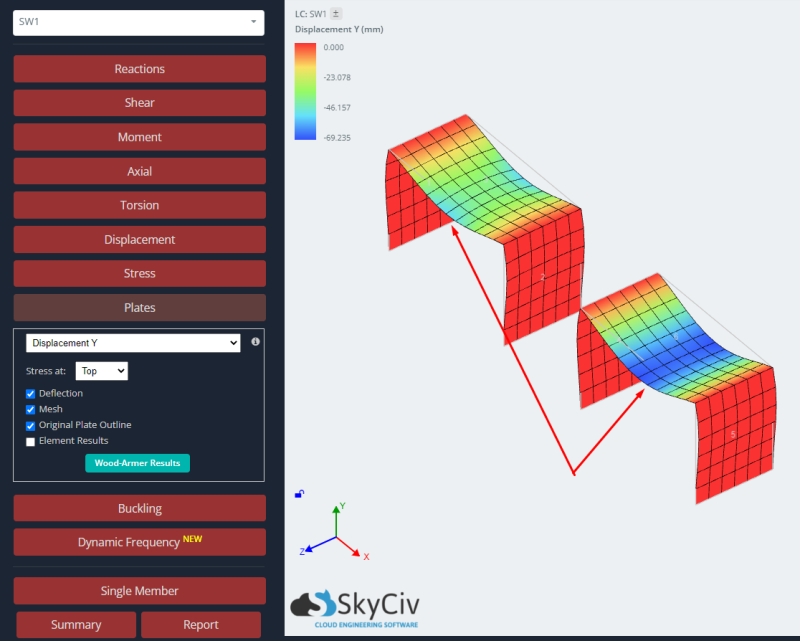
- Resultaten: Uiteindelijk, op dit punt bestuderen we de structurele respons voor beide platen, het isotrope en orthotrope geval. Voor meer details in het lezen van resultaten voor plaatanalyse, je kunt dit artikel bekijken Resultaten van plaatanalyse.

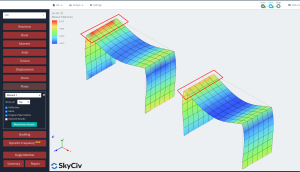
Om de reactie van beide gevallen te bestuderen, we vergelijken de resultaten van verticale verplaatsing en buigend moment. De orthotrope plaat vertoont kleinere doorbuigingen en grotere buigmomenten dan het isotrope geval. We kunnen zeggen dat het gebruik van een orthotrope benadering ons een stijver element zal geven en dit zal de globale en lokale resultaten beïnvloeden in een elastische lineaire analyse.
Ga gratis aan de slag
Uitchecken SkyCiv Structural 3D gratis vandaag om een voorproefje van onze software te krijgen!
Referenties:
- Chandrupatla, Tirupathi R & Belegundu, Ashok (2012). “Inleiding tot eindige elementen in de techniek” 4de editie, Pearson Onderwijs.
- W. Jiang en anderen (1997). “Eindige-elementenmodellering van verstijfde en niet-verstijfde orthotrope platen”, Computers & Structuren Vol.63, Nr.1, pp. 105-117, Elsevier Science Ltd.
- Torres Villavicencio et al (2013). “monografisch werk: Ontwerphulpmiddelen voor EMMEDUE-draagsystemen van gewapende betonnen panelen met E.P.S-kern (Systeem van geëxpandeerd polystyreen)”. Nationale Universiteit van Ingenieurswetenschappen.
- Alle softwarebeelden genomen van SkyCiv Structurele 3D-analysesoftware