Controleren of een kolom knikt
In deze korte tutorial, we zullen alles doornemen wat u moet weten over een eenvoudige kolom knikken analyse. Zoals we allemaal weten, kolommen zijn verticale elementen in een constructie die hoge axiale drukbelastingen ondergaan. Leden die worden onderworpen aan drukbelastingen kunnen een storingsmethode ervaren die wordt genoemd “Knikken” wat wordt beschreven als plotselinge zijwaartse afbuiging. Het is iets anders dan meegeven, maar we zullen dit tijdens de tutorial uitleggen.
Euler kniktheorie
De wiskundige Leonhard Euler onderzocht het gedrag van kolommen en leidde een eenvoudige formule af voor de belasting die nodig is om een kolom te buigen. Dit heet de kritische knikbelasting:

Dit is een vrij eenvoudige formule, echter, er zijn enkele belangrijke dingen om op te merken. Ten eerste, de doorsnede van een lid heeft twee traagheidsmomenten waarden (Iz en ikj), dus welke moet je kiezen? Nou, aangezien de formule zich bezighoudt met het vinden van de kritiek knikbelasting dan is het duidelijk dat we de laagste traagheidsmoment van de sectie, aangezien dat de laagste kritische knikbelasting oplevert (d.w.z. het zal eerder knikken). ten tweede, in plaats van de werkelijke lengte van het lid te gebruiken, L, we gebruiken in plaats daarvan de effectieve lengte van de kolom, KL. Dus wat is deze K-factor en waarom is deze nodig? We zullen dit in de volgende sectie bespreken.
Effectieve lengtefactoren (K)
Euler was een slimme kerel en hij kwam er snel achter dat de lengte van de kolom moet worden aangepast op basis van hoe deze aan beide uiteinden wordt beperkt of ondersteund. Om deze reden, we kunnen een factor gebruiken, K die de lengte aanpast om KL te geven. De theoretische en aanbevolen waarden voor de effectieve lengtefactor (K) worden gegeven in het onderstaande diagram:
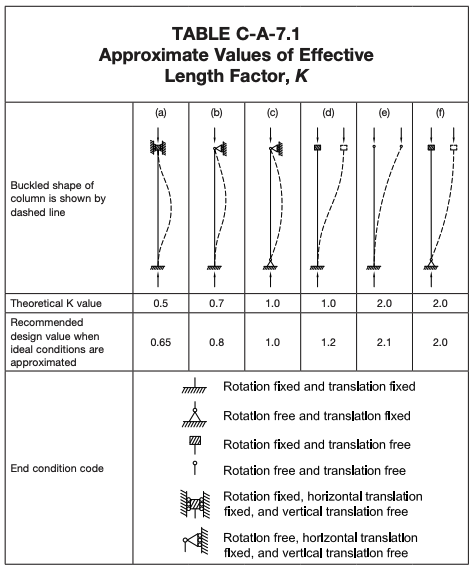
Bron: AISC 360-22: Specificatie voor constructieve stalen gebouwen
Knik versus opbrengst
Knikken en meegeven zijn twee verschillende vormen van falen. Yielding treedt op wanneer de spanning van een lid groter is dan de vloeigrens van het materiaal. Echter, knik kan optreden voordat buiging optreedt, afhankelijk van de situatie van de kolom. Bijvoorbeeld, als de kolommen’ kritische knikbelasting was 20 kN en zijn oppervlakte was slechts 1000 mm2 dan zou de kritische knikspanning zijn:
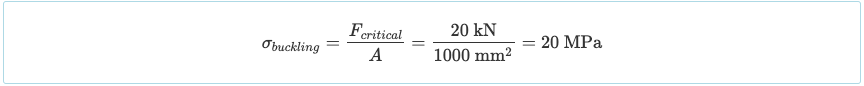
Omdat de kritische knikspanning lager is dan de vloeigrens van het materiaal (zeggen 300 MPa), dan zou het buigen voordat het bezwijkt.
Kolom knik voorbeeld
Laten we deze kennis gebruiken om een voorbeeld te doen:
Laten we zeggen dat ik een RHS-kolom van 100x20x3 mm heb die is gemaakt van constructiestaal (E = 200 GPa). Als het een lengte heeft van 3.0 meter en wordt aan de basis bevestigd en aan de bovenkant vastgemaakt, bij welke theoretische belasting zal het gaan knikken?
Met behulp van onze Gratis Traagheidsmoment Calculator we kunnen zien dat het laagste traagheidsmoment van de RHS-doorsnede I = is 45,172 mm4. Voor constructiestaal E = 200 GPa = 200 kN / mm2. Met behulp van de bovenstaande tabel kunnen we zien dat de effectieve lengtefactor voor een vastgespelde kolom K = is 0.7 en natuurlijk L = 3.0 m = 3000 mm. Daarom kunnen we de knikformule van Euler gebruiken:

Dus zodra de compressieve axiale kracht op het lid bereikt 20.22 kN en hoger zal de staaf in theorie knikken!
Ik hoop dat deze tutorial je heeft geholpen meer te begrijpen over het eenvoudig berekenen van kolomknik. Bekijk onze gratis kolomknikcalculator, Kolomcalculator of meld u vandaag nog aan om aan de slag te gaan met SkyCiv-software!


