Een volledig uitgewerkt voorbeeld van Eurocode 1 (IN 1991-1-4) berekeningen van windbelasting
In dit voorbeeld, we gaan de ontwerpwinddruk berekenen voor een magazijnstructuur in Aken, Duitsland. Onze referenties zijn de Eurocode 1 IN 1991-1-4 Actie op constructies (windlast) en DIN EN 1991-1-4 / NA:2010-12. We zullen een model van onze S3D gebruiken om te demonstreren hoe de belastingen op elk oppervlak worden toegepast.
Figuur 1. Magazijnmodel in SkyCiv S3D als voorbeeld.
Figuur 2. Site locatie (van Google Maps).
Tafel 1. Bouwgegevens nodig voor onze windberekening.
| Plaats | Aken, Duitsland |
|---|---|
| Bezetting | Diversen – Magazijnstructuur |
| Terrein | Vlakke landbouwgrond |
| Dimensies | 19.507 m (d) × 31.699 m (b) in plan Eave hoogte van 9.144 m Apex hoogte op hoogte. 10.973 m (h) Dakhelling 3:16 (10.62°) Zonder opening |
| Bekleding | Purlins op een afstand van 0.6 m Muurstijlen op afstand van elkaar 0.6 m |
De formule bij het bepalen van de ontwerpwinddruk is:
Voor basis windsnelheid:
\({v}_{b} = {c}_{aan u} {c}_{seizoen} {v}_{b,0}\) (1)
Waarbij:
\({v}_{b}\) = basis windsnelheid in m / s
\({c}_{aan u}\) = richtingsfactor
\({c}_{seizoen}\)= seizoensfactor
\({v}_{b,0}\) = fundamentele waarde van de basis windsnelheid (Nationale DIN-bijlage voor EN 1991-1-4)
Voor basissnelheidsdruk:
\({q}_{b} = 0.5 {⍴}_{lucht} {{v}_{b}}^{2} \) (2)
Waarbij:
\({q}_{b}\) = ontwerp winddruk in Pa
\({⍴}_{lucht}\) = dichtheid van lucht (1.25 kg / m3)
\({v}_{b}\)= basis windsnelheid in m / s
Voor piekdruk:
\({q}_{p}(z) = 0.5 [1 + 7 {l}_{v}(z)] {⍴}_{lucht} {{v}_{m}(z)}^{2} \) (3)
Waarbij:
\({v}_{m}(z)\) = gemiddelde windsnelheid, m / s = \({c}_{r}(z) {c}_{De}(z) {v}_{b}\) (4)
\({c}_{De}(z)\) = topografische factor
\({c}_{r}(z)\) = ruwheidsfactor:
\({c}_{r}(z) = {k}_{T} ln(\frac{z}{{z}_{0}}) : {z}_{min} ≤ {z} ≤ {z}_{max}\) (5)
\({c}_{r}(z) = {c}_{r}({z}_{min}) : {z} ≤ {z}_{min}\) (6)
Waarbij:
\({z}_{0}\) = ruwheid lengte, m
\({k}_{T}\) = terrein factor, afhankelijk van de ruwheidslengte, \({z}_{0}\) berekend met:
\({k}_{T} = 0.19 {(\frac{{z}_{0}}{{z}_{0,II}})}^{0.07} \) : \( {z}_{0,II} = 0.05\) (terreincategorie II) (7)
\({z}_{min}\) = minimale hoogte
\({z}_{max}\) = maximale hoogte genomen als 200 m.
Uit deze vergelijkingen (4) naar (7), DIN EN 1991-1-4/NA:2010-12 Bijlage B vat de formule voor elke parameter samen, afhankelijk van de terreincategorie:
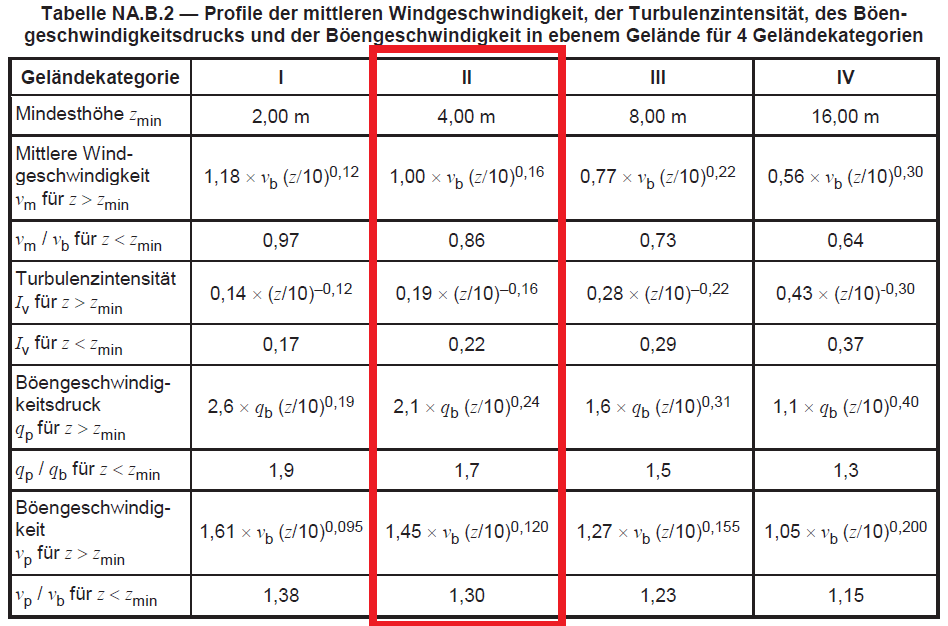
Figuur 3. Tabel NA.B.2 van DIN EN 1991-1-4 / NA:2010-12.
Elke parameter wordt hierna besproken.
Terreincategorie
De structuur is gelegen op landbouwgrond, die is geclassificeerd als Terreincategorie II zoals gedefinieerd in bijlage A van EN 1991-1-4 en tabel NA.B-1 van de nationale DIN-bijlage.
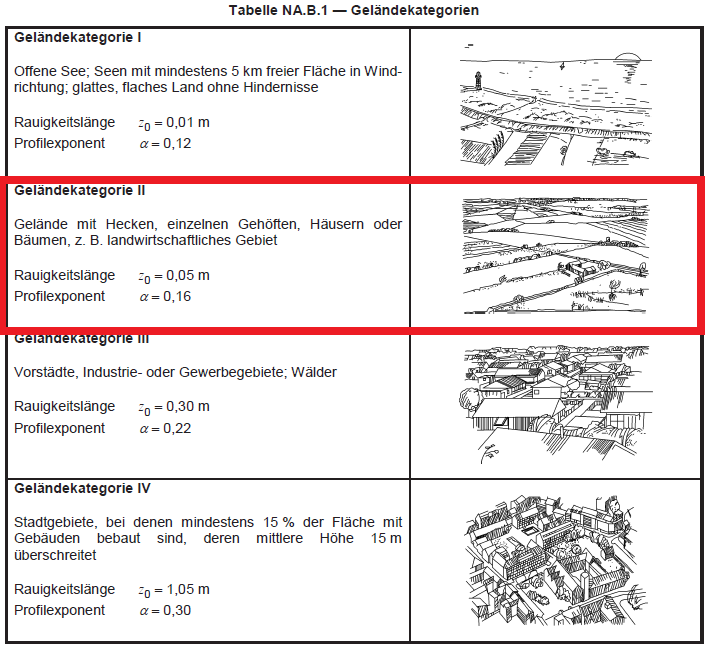
Figuur 4. Tabel NA.B.1 van DIN EN 1991-1-4 / NA:2010-12.
Richtings- en seizoensfactoren, \({c}_{aan u}\) & \({c}_{seizoen}\)
Om te berekenen voor vergelijking (1), we moeten de richtinggevende en seizoensfactoren bepalen, \({c}_{aan u}\) & \({c}_{seizoen}\). Nationale DIN-bijlage voor EN 1991-1-4 vereenvoudigt deze berekening omdat de voorgestelde waarden van deze factoren gelijk zijn aan 1.0.
Basis windsnelheid en -druk, \({v}_{b,0}\) & \({q}_{b,0}\)
Zoals eerder gezegd, windsnelheidskaart voor Duitsland kan worden gehaald uit de nationale DIN-bijlage voor EN 1991-1-4. Elk Europees land heeft een aparte nationale bijlage waarin het de voorgestelde windbelastingparameters van EN kalibreert 1991-1-4.
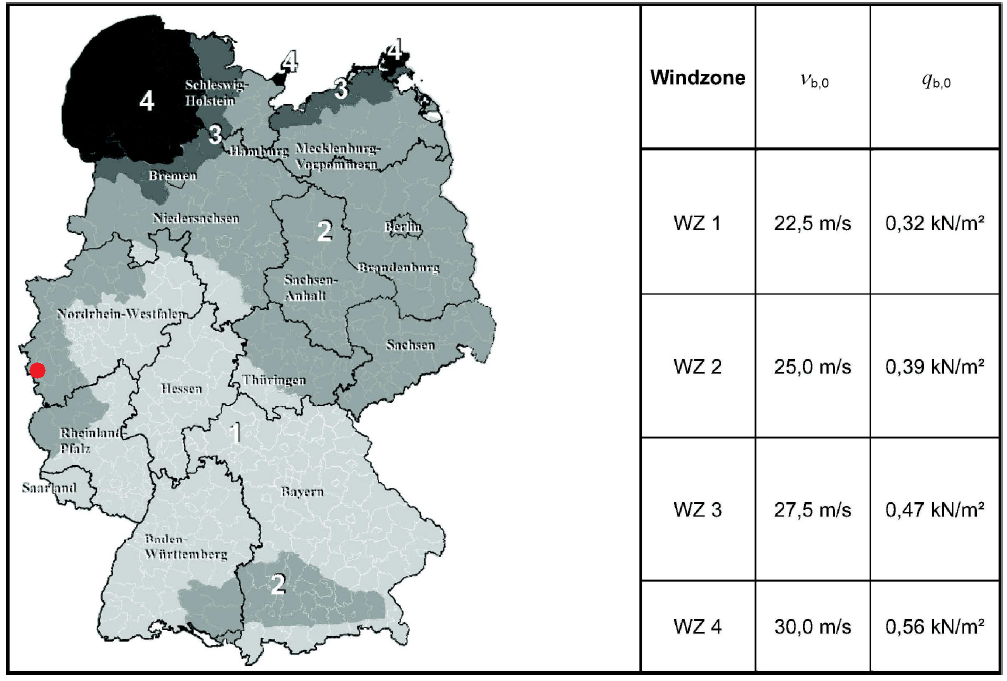
Figuur 5. Tabel NA.A.1 van DIN EN 1991-1-4 / NA:2010-12.
Voor onze sitelocatie, Aken, Duitsland ligt in WZ2 met \({v}_{b,0}\) = 25.0 Mevrouw zoals weergegeven in bovenstaande afbeelding. Van deze waarde, sinds \({c}_{aan u}\) & \({c}_{seizoen}\) zijn beide gelijk aan 1.0, kunnen we de basis winddruk berekenen, \({q}_{b,0}\), met behulp van vergelijkingen (1) en (2). Vandaar, de overeenkomstige waarde van \({q}_{b,0}\) = 0.39 kPa, ook aangegeven in de windkaart van DIN Nationale bijlage voor EN 1991-1-4.
SkyCiv automatiseert nu de detectie van het windgebied en het verkrijgen van de bijbehorende windsnelheid met slechts een paar invoer. Proberen onze SkyCiv Free Wind Tool
Gemiddelde windsnelheid, \({v}_{m}(z)\)
Om de piekdruk te berekenen, \({q}_{p}(z)\), we moeten de waarde van de gemiddelde windsnelheid bepalen, \({v}_{m}(z) \). Van figuur 3, we kunnen de gemiddelde snelheid berekenen, \({v}_{m}(z) \):
Voor \({z}_{min} ≤ {z} ≤ {z}_{max} : 1.0 {v}_{b} {(0.1z)}^{0.16} \)
Voor \({z}_{min} ≤ {z} ≤ {z}_{max} : 0.86 {v}_{b} \)
Piekdruk, \({q}_{p}(z)\)
Evenzo, de piekdruk, \({q}_{p}(z)\), kan worden opgelost met behulp van figuur 3:
Voor \({z}_{min} ≤ {z} ≤ {z}_{max} : 2.1 {q}_{b} {(0.1z)}^{0.24} \)
Voor \({z} ≤ {z}_{min} : 1.7 {q}_{b} \)
Om de piekdruk te berekenen, \({q}_{p}(z) \), we moeten de waarde van de gemiddelde windsnelheid bepalen, \({v}_{m}(z) \). Van figuur 3, we kunnen de gemiddelde snelheid berekenen, \({v}_{m}(z) \):
voor \({z}_{min} ≤ {z} ≤ {z}_{max} : 1.0 {v}_{b} {(0.1z)}^{0.16} \)
voor \({z} ≤ {z}_{min} : 0.86 {v}_{b} \)
Resultaten voor gemiddelde windsnelheid en piekdruk voor elk niveau worden weergegeven in de tabel 2 hieronder.
Tafel 2. Berekende gemiddelde windsnelheid en piekdruk voor elk niveau van de constructie.
| hoogte / niveau | \({v}_{m}(z)\), Mevrouw | \({q}_{p}(z)\), Goed |
|---|---|---|
| 3.00 | 21.5 | 664.06 |
| 6.00 | 23.04 | 725.66 |
| 9.00 | 24.58 | 799.83 |
| 10.97 (h) | 25.37 | 838.80 |
Externe winddruk, \({w}_{e}\)
Bij berekening van piekdruk, \({q}_{p}(z)\), de externe winddruk die op het oppervlak van de constructie werkt, kan worden opgelost met:
\({w}_{e} = {q}_{p}(z) {c}_{Aan}\) (8)
Waarbij:
\({w}_{e}\) = externe winddruk, Goed
\({q}_{p}(z)\) = piekdruk, Goed
\({c}_{Aan}\) = drukcoëfficiënt voor buitenoppervlak
een) Verticale muren
Voor verdeling van windwaartse druk (Zone D), Sectie 7.2.2 of EN 1991-1-4 beschrijft hoe het moet worden verspreid, afhankelijk van \(h ), \(b\), en \(d\). Voor ons voorbeeld, wij hebben \(h < b\) (10.973 < 31.699m), Vandaar, \({z}_{e} = h\) zoals te zien in figuur 6.
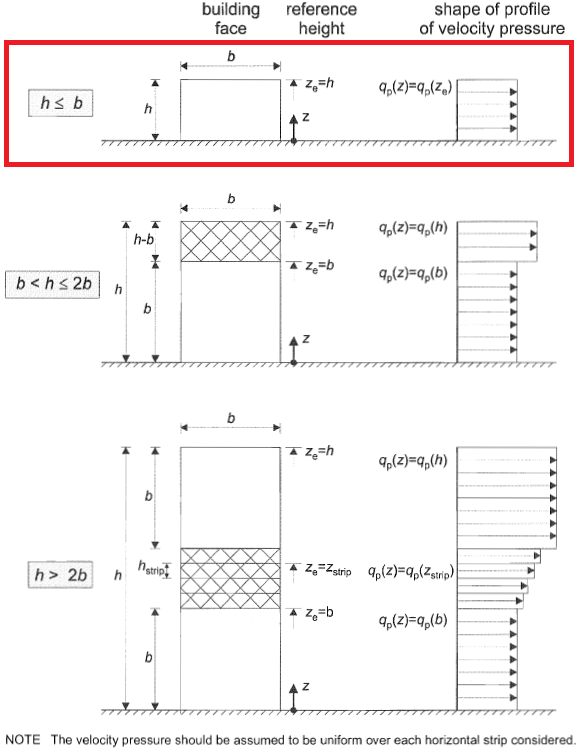
Figuur 6. Drukverdeling voor windmuur gebaseerd op figuur 7.4 of EN 1991-1-4.
Anderzijds, drukverdeling voor zijwanden (Zones A tot C) worden getoond in Figuur 7.5 of EN 1991-1-4 en hangt af van de \(e = b < 2h ). Voor ons voorbeeld, de waarde van \(e = 21.946\), Vandaar, \(e > d\) zoals te zien in figuur 7. Bovendien, lijwaartse wanddruk wordt aangeduid als Zone E. Externe drukcoëfficiënten worden dan aangegeven in figuur 8 gebaseerd op tabel NA.1 van DIN EN 1991-1-4 / NA:2010-12.
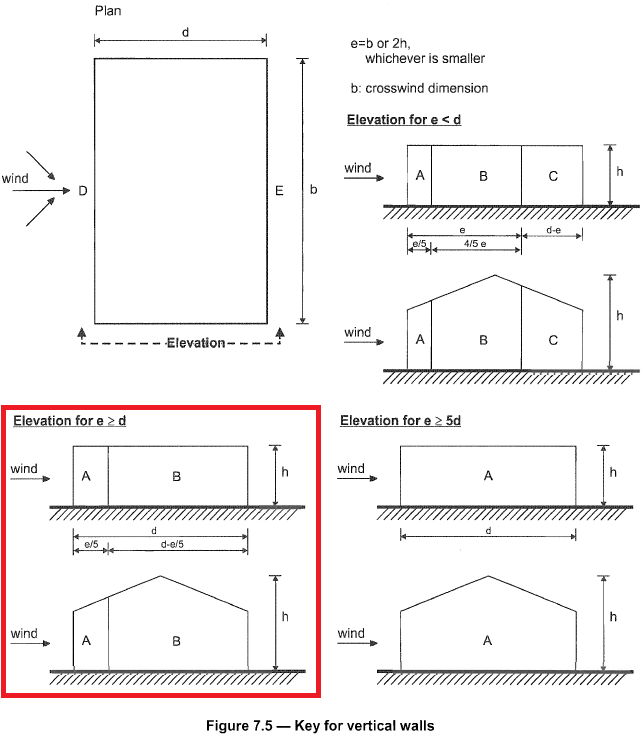
Figuur 7. Drukverdeling voor zijwand op basis van figuur 7.5 of EN 1991-1-4.
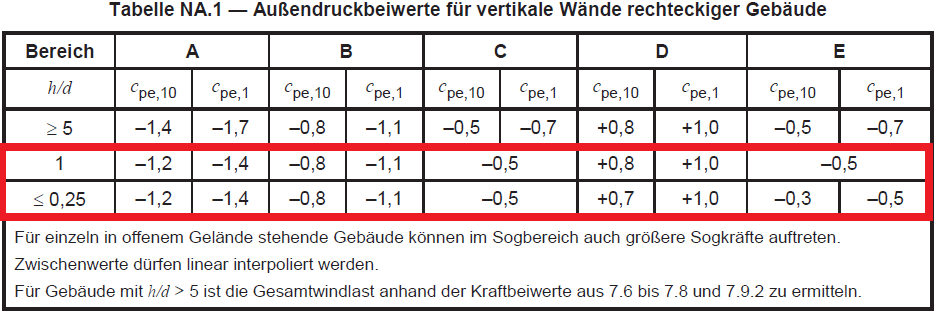
Figuur 8. Externe drukcoëfficiënt voor verticale wanden (Zones A tot E) gebaseerd op tabel NA.1 van DIN EN 1991-1-4 / NA:2010-12.
Sinds \(h / d = 0.563\), we zullen de informatie moeten interpoleren \({c}_{Aan}\) waarden om te berekenen voor de ontwerpwinddruk. De abonnementen voor \({c}_{Aan,10}\) en \({c}_{Aan,1}\) betekent dat de waarde afhankelijk is van het gebied waar de winddruk wordt uitgeoefend, voor zowel 1 m². en 10 m². Meestal, voor gebouwen, \({c}_{Aan,10}\) is sindsdien aangenomen \({c}_{Aan,1}\) wordt gebruikt voor kleine elementen zoals bekledingen en dakelementen. De geïnterpoleerde waarden voor \({c}_{Aan}\) worden weergegeven in de tabel 3 hieronder.
Tafel 3. Berekende externe drukcoëfficiënt voor verticale wanden.
| \(h / d ) | A | B | C | D | E |
|---|---|---|---|---|---|
| 1.000 | -1.2 | -0.8 | -0.5 | 0.8 | -0.5 |
| 0.563 | -1.2 | -0.8 | -0.5 | 0.742 | -0.383 |
| 0.250 | -1.2 | -0.8 | -0.5 | 0.7 | -0.3 |
b) Dak
De verdeling van de ontwerpwinddrukken voor het dak wordt gedetailleerd in secties 7.2.3 naar 7.2.10 en 7.3 of EN 1991-1-4. Concreet, aangezien het dakprofiel van onze structuur duopitch is, we zullen sectie gebruiken 7.2.5 om de externe drukcoëfficiënten van het dak te krijgen, \({c}_{Aan}\), zoals te zien in figuur 9 en 10 hieronder.
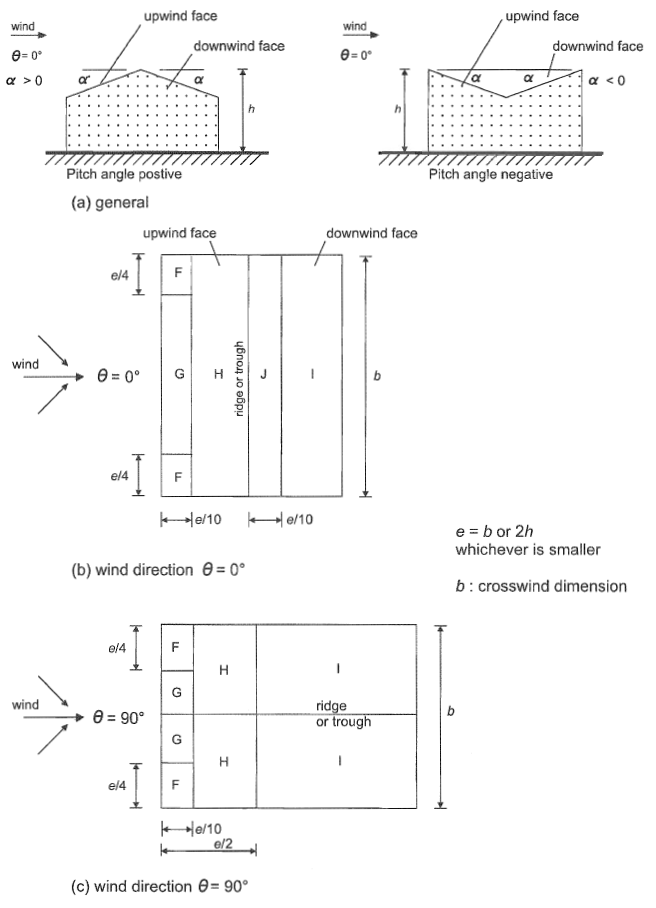
Figuur 9. Drukverdeling voor duopitch-dak op basis van figuur 7.8 of EN 1991-1-4.
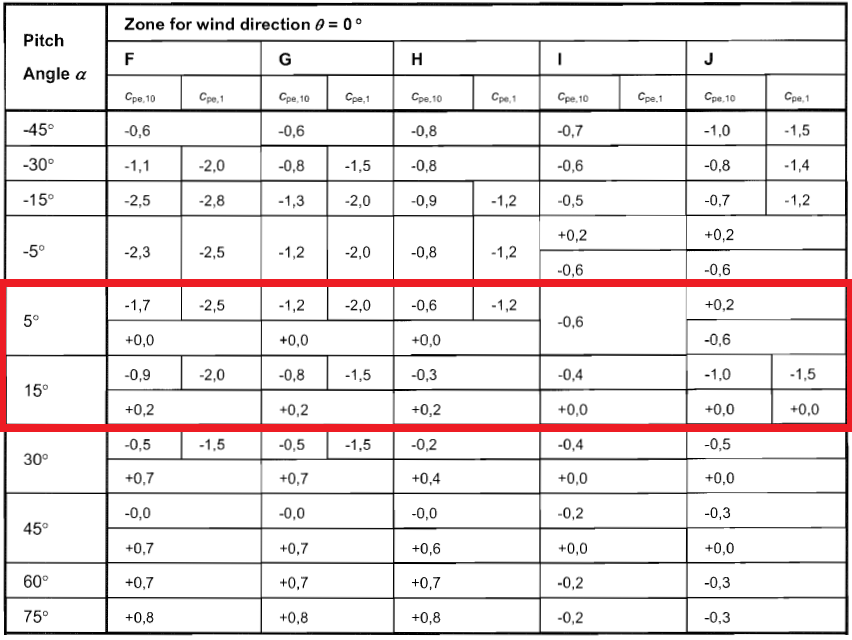
Figuur 9. Externe drukcoëfficiënt voor dakoppervlakken muren (Zones F tot J) gebaseerd op tabel 7.4a van EN 1991-1-4.
Omdat de dakhellingshoek gelijk is aan 10,62 °, we moeten de \({c}_{Aan}\) waarden van 5 ° en 15 °. Vandaar, de berekende \({c}_{Aan}\) waarden voor onze structuur worden weergegeven in de tabel 4 hieronder.
Tafel 4. Berekende externe drukcoëfficiënt voor dakoppervlakken.
| \(h / d ) | Zone F | Zone G | Zone H | Zone I | Zone J | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| \(-{c}_{de}\) | \(+{c}_{de}\) | \(-{c}_{de}\) | \(+{c}_{de}\) | \(-{c}_{de}\) | \(+{c}_{de}\) | \(-{c}_{de}\) | \(+{c}_{de}\) | \(-{c}_{de}\) | \(+{c}_{de}\) | |
| 5.00 | -1.7 | 0.0 | -1.2 | 0.0 | -0.6 | 0.0 | -0.6 | – | -0.6 | 0.2 |
| 10.62 | -1.250 | 0.112 | -0.975 | 0.112 | -0.431 | 0.112 | -0.488 | – | -0.825 | 0.088 |
| 15.00 | -0.9 | 0.2 | -0.8 | 0.2 | -0.3 | 0.2 | -0.4 | – | -1.0 | 0.0 |
Interne winddruk, \({w}_{ik}\)
Interne winddruk, \({w}_{ik}\), kan zich ontwikkelen en werkt gelijktijdig met de externe winddruk. Vandaar, de noodzaak om te berekenen \({w}_{ik}\) is noodzakelijk. De formule om te berekenen \({w}_{ik}\) is:
\({w}_{ik} = {q}_{p}(z) {c}_{pi}\) (9)
Waarbij:
\({w}_{ik}\) = interne winddruk, Goed
\({q}_{p}(z)\) = piekdruk, Goed
\({c}_{pi}\) = interne drukcoëfficiënt
Sectie 7.2.9 of EN 1991-1-4 zegt dat \({c}_{pi}\) kan worden opgevat als de zwaarste van +0.2 en -0.3. We gaan ervan uit dat onze structuur geen dominante opening heeft.
Ontwerp winddruk
Met deze \({c}_{Aan}\) en \({c}_{pi}\) waarden, we kunnen nu de overeenkomstige externe winddruk voor elke zone berekenen, zoals weergegeven in de tabel 5.
Tafel 5. Berekende externe winddruk per oppervlak.
| Oppervlakte | Zone | \({w}_{e}\) | \({w}_{ik}\) | Gecombineerd \({w}_{e}\) en \({w}_{ik}\) | |||
|---|---|---|---|---|---|---|---|
| \(-{c}_{Aan}\) | \(+{c}_{Aan}\) | \(+{c}_{pi}\) | \(+{c}_{pi}\) | min waarde | maximum waarde | ||
| Muur | Zone A | -1006.56 | 167.76 | -251.64 | -1174.32 | 754.92 | |
| Zone B | -671.04 | – | -838.80 | -419.40 | |||
| Zone C | -419.40 | – | -587.16 | 167.76 | |||
| Zone D | – | 622.11 | 454.35 | 873.75 | |||
| Zone E | -321.54 | – | -489.30 | -69.9 | |||
| Dak | Zone F | -1048.83 | 94.28 | -1216.59 | 345.92 | ||
| Zone G | -818.00 | 94.28 | -985.76 | 345.92 | |||
| Zone H | -361.86 | 94.28 | -529.62 | 345.92 | |||
| Zone I | -409.00 | -576.76 | -157.36 | ||||
| Zone J | -691.84 | 73.48 | -859.60 | 325.12 | |||
Van deze waarden, we kunnen deze ontwerpwinddrukken nu toepassen op onze constructie. Gezien één framebaai (innerlijk), de gecombineerde \({w}_{e}\) en \({w}_{ik}\) is als volgt:
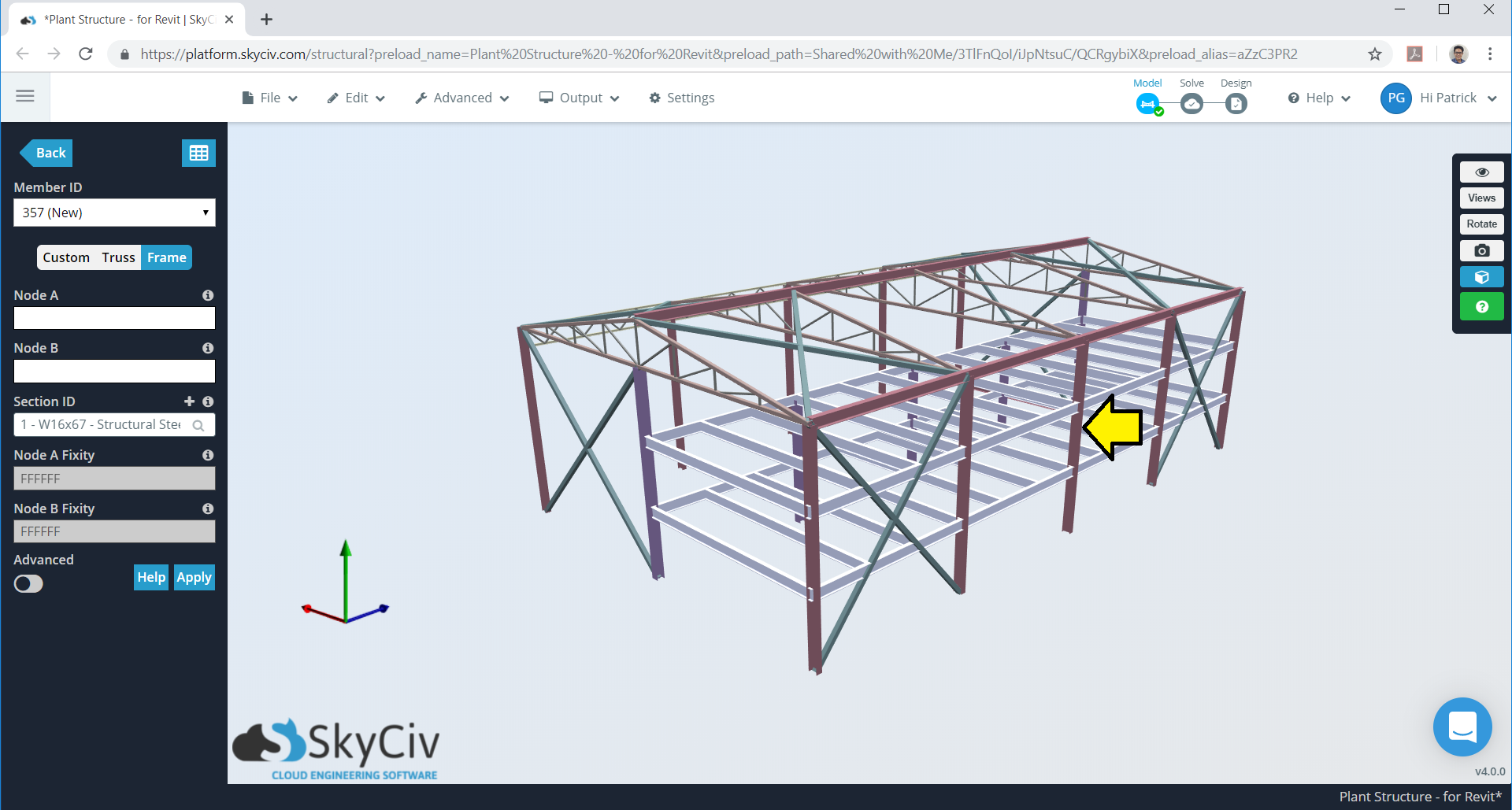
Figuur 10. Binnenframe te overwegen.
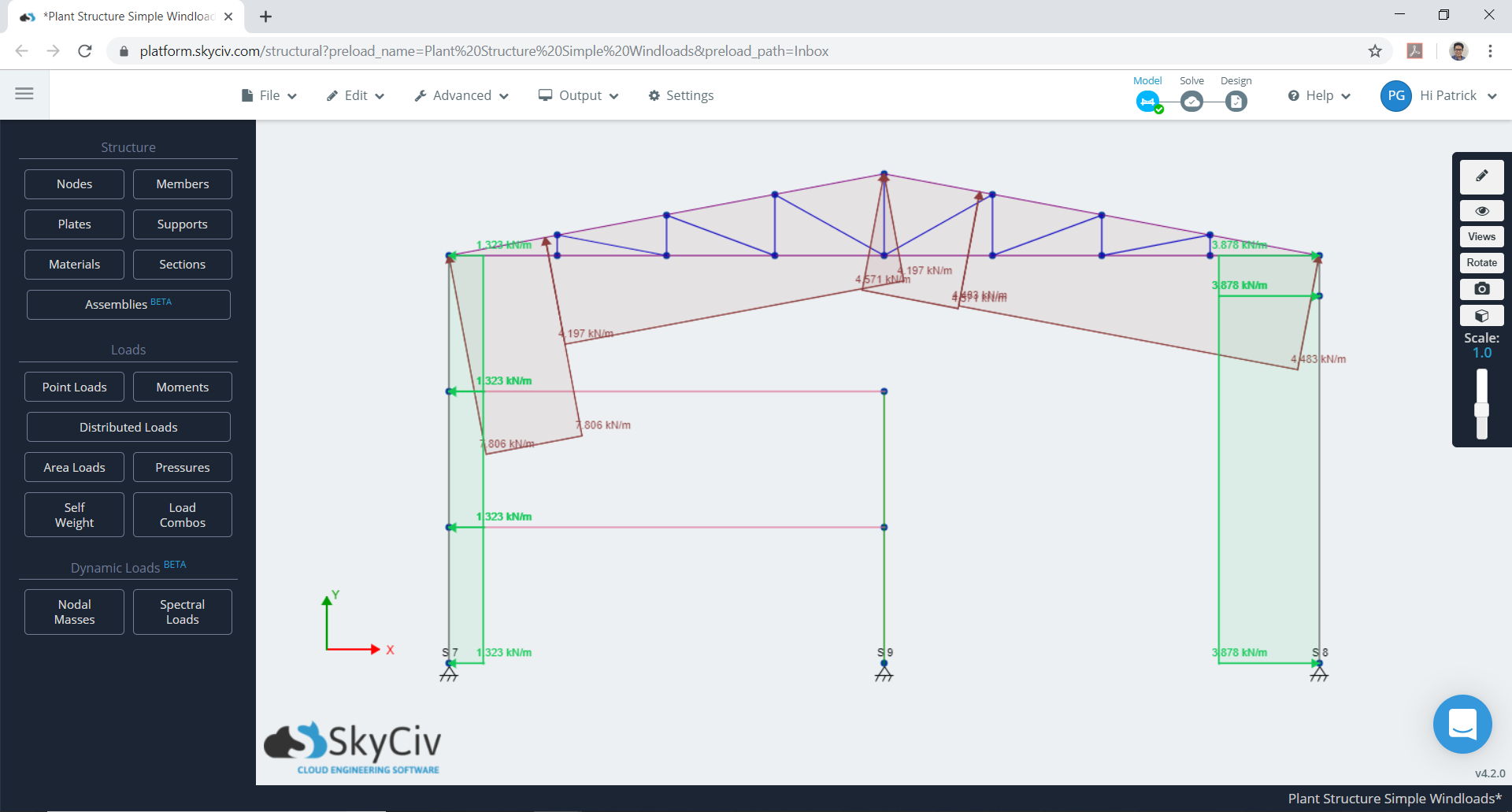
Figuur 11. Minimumgeval voor gecombineerd \({w}_{e}\) en \({w}_{ik}\).
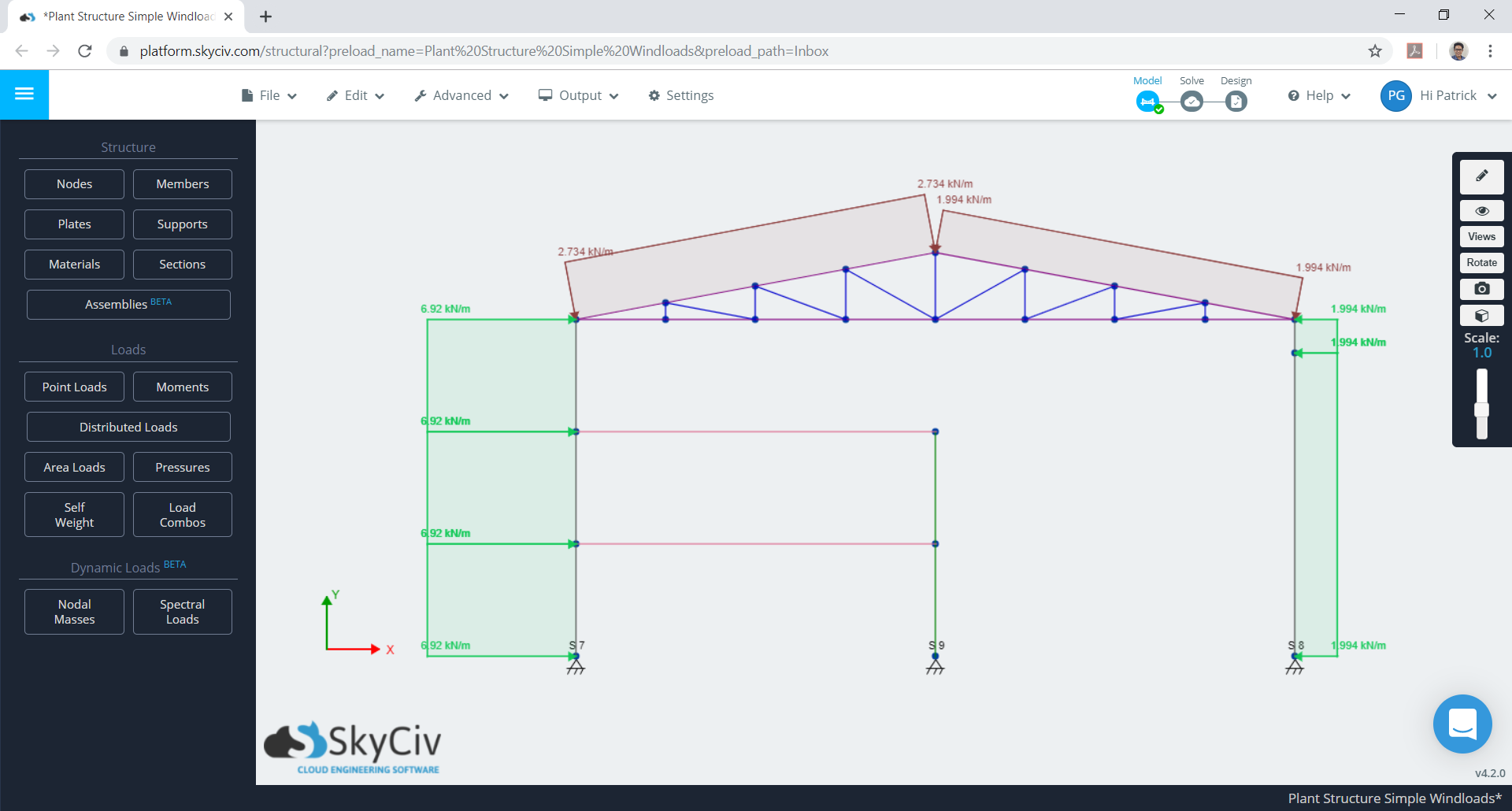
Figuur 12. Maximale case voor gecombineerd \({w}_{e}\) en \({w}_{ik}\).
Deze berekeningen kunnen allemaal worden uitgevoerd met SkyCiv's software voor windbelasting voor ASCE 7-10, 7-16, IN 1991, NBBC 2015 en AS 1170. Gebruikers kunnen een locatie op een site invoeren om windsnelheden en topografische factoren te krijgen, voer gebouwparameters in en genereer de winddrukken. Met een professioneel account, gebruikers kunnen dit automatisch toepassen op een structureel model en structurele analyse uitvoeren in één software.
Anders, proberen onze SkyCiv Free Wind Tool voor berekeningen van windsnelheid en winddruk op eenvoudige constructies.
Bouwkundig ingenieur, Product ontwikkeling
MS Civiele Techniek
Referenties:
- In, B. (2005). Eurocode 1: Acties op constructies - deel 1-4: Algemene acties - Windacties.
- DIN EN 1991-1-4. (2005). Eurocode 1: Acties op constructies deel 1-4: Algemene acties, Windlasten; Duitse versie EN 1991-1-4: 2005.



