Een doorloop en voorbeeld van het berekenen van sneeuwdriftbelastingen en hoe deze toe te passen
Dakontwerpen hebben meestal veel dakverhogingen en bieden zelden een enkele dakhoogte. Door dit, er zijn dakvlakken hoger en lager dan elkaar en zijn onderhevig aan sneeuwverstuivingen. De hoeveelheid extra sneeuwbelasting, of toeslag, kan en zal een grote impact hebben op het ontwerp van de leden op deze gebieden.
Geometrie van het dak en de richting van de wind zijn de twee drijfveren die tot sneeuwverschuivingen leiden. De twee windrichtingen die sneeuwafwijkingen veroorzaken zijn: “loef” en “loef-”. Bovenwindse sneeuwafwijkingen treden op wanneer de wind sneeuw van een lager gelegen dak naar de muur van een aangrenzend dak blaast, hoger dak. Benedenwindse sneeuwafwijkingen treden op wanneer de wind sneeuw van een hoger gelegen dak naar beneden blaast op een aangrenzend lager dak. Zie figuur 7-7 van ASCE 7-10 hieronder voor een beknopte weergave:

Laten we aannemen dat ons project in Madison is, Wisconsin en we hebben onze gebalanceerde al berekend, sneeuwbelasting op het dak hier. Van ons voorbeeld, onze grondbelasting en sneeuwbelasting op plat dak bleken te zijn 30 psf en 21 psf, respectievelijk. Bepalingen over het berekenen van de sneeuwdrifttoeslag voor constructies zijn te vinden in sectie 7.8 van ASCE 7-10.
Het dak van onze voorbeeldconstructie heeft twee verschillende dakhoogten en daarom moeten we de sneeuwdrifttoeslag berekenen en toepassen op onze leden. In ons geval, onze balken zijn verdeeld op 10 voeten.
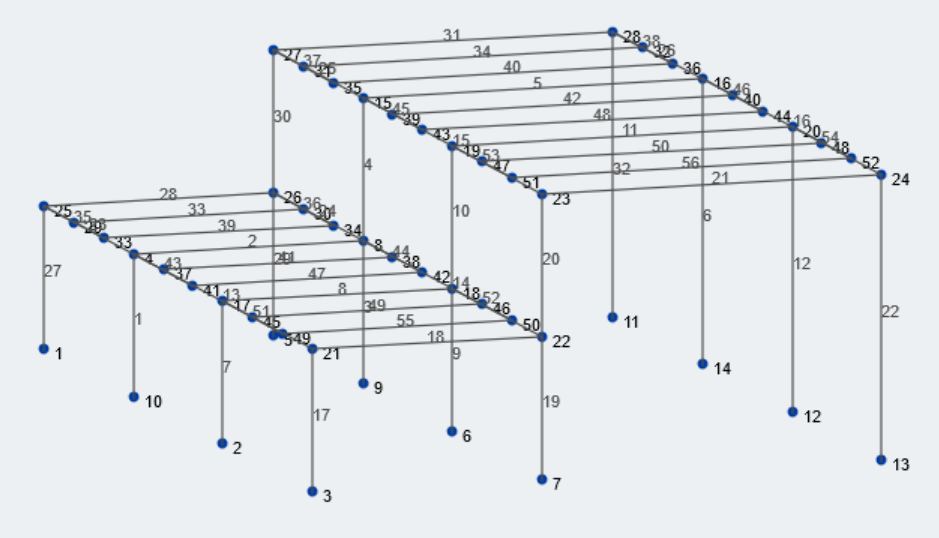
Figuur 1: Isometrische weergave van onze voorbeeldstructuur
Laten we eerst de relevante geometrische informatie over onze structuur verzamelen. De grootte van de onderste baai en de bovenste baai is: 25 voeten en 37 voeten, respectievelijk. De lagere en hogere dakverhogingen zijn: 15 voeten en 30 voeten van leerjaar, respectievelijk. De meeste geometrische waarden kunnen aan variabelen worden gekoppeld. Laten we eens kijken naar alle relevante variabelen voor deze berekening.
\({p}_{g}\) We zullen de zonnepaneelstructuur beschouwen als een gebouw met monoslope dak en
\({l}_{u}\) = lengte bovendak
\({l}_{l}\) = lengte onderdak
\({h}_{d}\) = hoogte van sneeuwafwijking
\({w}\) = breedte van sneeuwafwijking
\({h}_{b}\) = hoogte van uitgebalanceerde sneeuwbelasting
\({h}_{c}\) = vrije hoogte vanaf de bovenkant van de uitgebalanceerde sneeuwbelasting tot het dichtstbijzijnde punt van het aangrenzende dak
\({h}_{r}\) = hoogteverschil tussen daken
\({p}_{s}\) = ontwerp sneeuwbelasting uit hoofdstuk 7
\({c}\) = sneeuwdichtheid
\({p}_{d}\) = sneeuw drift belasting
Kijk eens naar figuur 7-8 van ASCE 7-10 voor een weergave van veel van deze termen en wat ze visueel vertegenwoordigen:
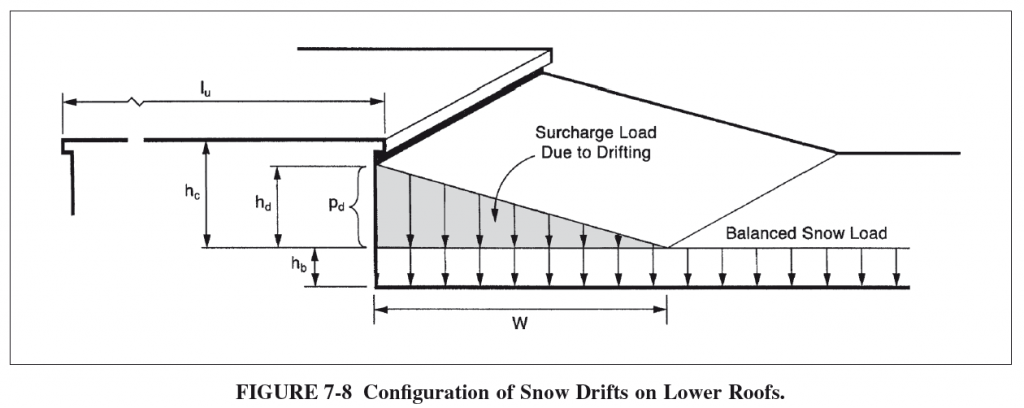
De sneeuwdrifttoeslag vinden
Nu we hebben vastgesteld wat de variabelen zijn, de configuraties voor het laden van sneeuw, en de geometrische beperkingen van onze structuur, laten we de sneeuwafwijking berekenen.
Eerste, zoeken of het laden van sneeuwdrift nodig is, voor ASCE 7.7-1:
kan worden aangenomen dat \({h}_{c}/{h}_{b} < 0.2\), dan is sneeuwdrifttoepassing niet nodig.
\({h}_{b} = {p}_{s}/{c}\), waar:
\({c} = 0.13{p}_{g} + 14 ≤ 30 pcf)
\({c} = 0.13*(30) + 14 = 17.9 pcf 30 pcf \)
\({h}_{b} = {21 psf}/{17.9 pcf} = 1.17 [object Window])
\({h}_{c} = {h}_{r}-{h}_{b}\)
\({h}_{c} = 15 ft – 1.17 Voor het zijbelastingsgeval 13.8 [object Window])
\({h}_{c}/{h}_{b} = 13.8 ft/1.17ft = 11.8 > 0.2\) en daarom, sneeuw drift laden is noodzakelijk.
Voor het zijbelastingsgeval, vind maximale drifthoogte tussen zowel loef- als lijwaartse richtingen:
De hoogte van de drift voor beide windrichtingen kan worden gevonden met behulp van de vergelijking in figuur 7-9 van ASCE 7-10, hieronder weergegeven:
\({h}_{d} = 3/4*(0.43({l}_{l})^{1/3}({p_g}+10)^{1/4}-1.5)\) voor windwaartse drift
\({h}_{d} = 0.43({l}_{u})^{1/3}({p_g}+10)^{1/4}-1.5\) voor lijwaartse drift
Windwaartse drifthoogte:
\({h}_{d} =3/4*(0.43(25 ft)^{1/3}(30 psf+10)^{1/4}-1.5)\)
\({h}_{d} = 1.25 [object Window])
Benedenwaartse drifthoogte:
\({h}_{d} = 0.43(37 ft)^{1/3}(30 psf+10)^{1/4}-1.5\)
\({h}_{d} = 2.1 [object Window])
De maximale drifthoogte tussen de loef- en lijwaartse drifthoogte wordt gebruikt voor het ontwerp, daarom:
\({h}_{d} = 2.1 [object Window])
De volgende, vind de breedte van de sneeuwdrifttoeslag:
De breedte van de sneeuwafwijkingsbelasting:, \({w}\), hangt af van \({h}_{c}\) en \({h}_{d}\)
Per sectie 7.7.1,
kan worden aangenomen dat \({h}_{d} ≤ {h}_{c}\), vervolgens \({w} = 4{h}_{d}\)
kan worden aangenomen dat \({h}_{d} > {h}_{c}\), vervolgens \({w} = 4{h}_{d}^2/{h}_{c}) en vervolgens \({h}_{d} = {h}_{c}\)
In ons geval, \({h}_{c} = 13.8 [object Window]) en \({h}_{d} = 2.1 [object Window]), en daarom:
\({h}_{d} ≤ {h}_{c}\), en
\({w} = 4*(2.1 ft)\)
\({w} = 8.4 [object Window])
Notitie, voor ASCE 7-10 de de sneeuwafwijkingsbreedte mag nooit groter zijn dan \(8{h}_{c}\)
Laatst, bereken de sneeuw drift toeslag belasting:
Om de maximale toeslag te vinden, vermenigvuldig de drifthoogte met de sneeuwdichtheid:
\({p}_{d} = {h}_{d}{c}\)
In ons geval,
\({p}_{d} = (2.1 ft)*(17.9 pcf)\)
\({p}_{d} = 37.6 [object Window])
De maximale sneeuwdrifttoeslag wordt dan gesuperponeerd op de uitgebalanceerde sneeuwbelasting:
\({p}_{max} = {p}_{d}+{p}_{s}\)
\({p}_{max} = 58.6 [object Window])
De sneeuwdrifttoeslag toepassen
Laten we eens kijken naar het middelste frame van onze structuur. Het verdeelde oppervlak voor de liggers in dit vlak is 10 ft vanwege de constante 10 ft straalafstand. Figuur 2 hieronder weergegeven geeft de evenwichtige sneeuwbelasting weer van: 21 psf toegepast op het dak van onze structuur. Notitie, alle waarden zijn niet-factored, dienstladingen.
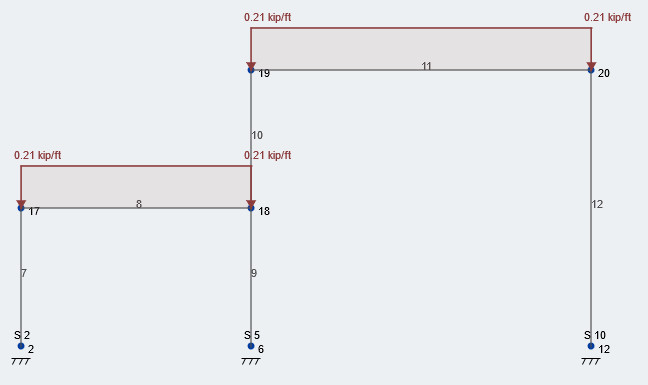
Figuur 2: Typische beladingstoestand van uitgebalanceerde sneeuwbelasting
Nu, laten we de sneeuwdrifttoeslag nemen en deze op onze structuur leggen. Figuur 3 geeft de extra driftbelasting op de juiste locatie weer. Zoals je kunt zien, onze totale sneeuwbelasting is 58.6 psf – afgerond naar boven 59 psf – bevindt zich aan de voorkant van de muur en neemt dan lineair af over de 8.4 ft driftbreedte terug naar de constante uitgebalanceerde sneeuwbelasting. Deze beladingstoestand volgt de gehele lengte van de wand, in onze cursus, de lengte van de structuur.
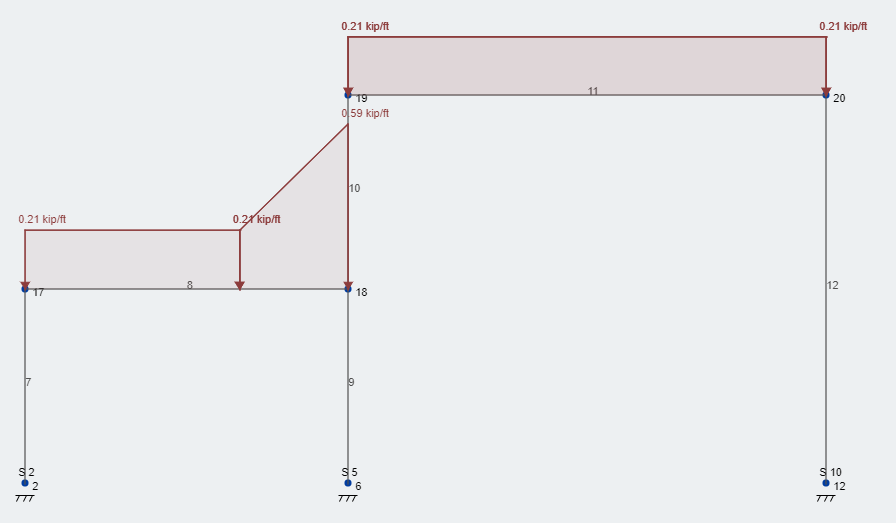
Figuur 3: Typische beladingstoestand serviceniveau sneeuwontwerpbelastingen
Op dit punt zijn de sneeuwbelastingen klaar voor analyse in samenhang met andere belastinggevallen en belastingcombinaties op basis van ASCE 7-10 en andere relevante bouwvoorschriften. Lees hoofdstuk 7 van ASCE 7-10 voor meer informatie over opeenvolgende bepalingen voor gedeeltelijke sneeuwbelasting en ongebalanceerde sneeuwbelasting, aangezien die voorwaarden hier niet zijn geëvalueerd.
Referenties:
- Minimale ontwerpbelastingen voor gebouwen en andere constructies. (2013). ASCE / SEI 7-10. American Society of Civil Engineers.


