Berekeningsvoorbeeld van het kantelmoment – Gewapende betonnen cantilever

Dit is een eenvoudige handleiding voor het berekenen van het kantelmoment in een keermuur met voorbeelden. De eerste stabiliteitscontrole die wordt uitgevoerd voor een vrijdragende betonnen keermuur is tegen kantelen. Het verwijst naar het vermogen van de weerstandskrachten om te voorkomen dat de muur roteert ten opzichte van de meest linkerbenedenhoek van de basis voor de werking van de kantelkrachten. Die twee belastingsgroepen (weerstand bieden en omverwerpen) zijn als volgt verdeeld::

Weerstand tegen belastingen:

• Zelfgewicht keermuur
• Actieve grond boven het hielgewicht
• Toeslag:

Lasten kantelen:

• Actieve bodem zijwaartse druk
• Zijdelingse druk die het gevolg is van de aanwezigheid van de toeslag

Dat gezegd hebbende, het berekeningsproces zal in het volgende worden gedetailleerd::

Invoergegevens:

Stang

• Hoogte: 3.124 m
• Breedte: 0.305 m
• offset: 0.686 m

Baseren

• Breedte: 2.210 m
• Dikte: 0.381 m

Actieve en passieve bodem

• Gewichtseenheid: 18.85 kN / m³
• Wrijvingshoek: 35 graden

Onderbouw Bodem

• Gewichtseenheid: 18.85 kN / m³
• Wrijvingshoek: 35 graden
• Grond-beton wrijvingscoëfficiënt: 0.55
• Toegestane lagerdruk: 143.641 kPa

Bodemlagen:

• Actief: 3.505 m
• Passief: 0.975 m
• Onderbouw: 0.792 m

Toeslag laadwaarde: -17.237 kN / m

Verticale belastingen:

Alle verticale belastingen waaraan de betonnen vrijdragende keermuur wordt blootgesteld, worden weergegeven in de volgende afbeelding::

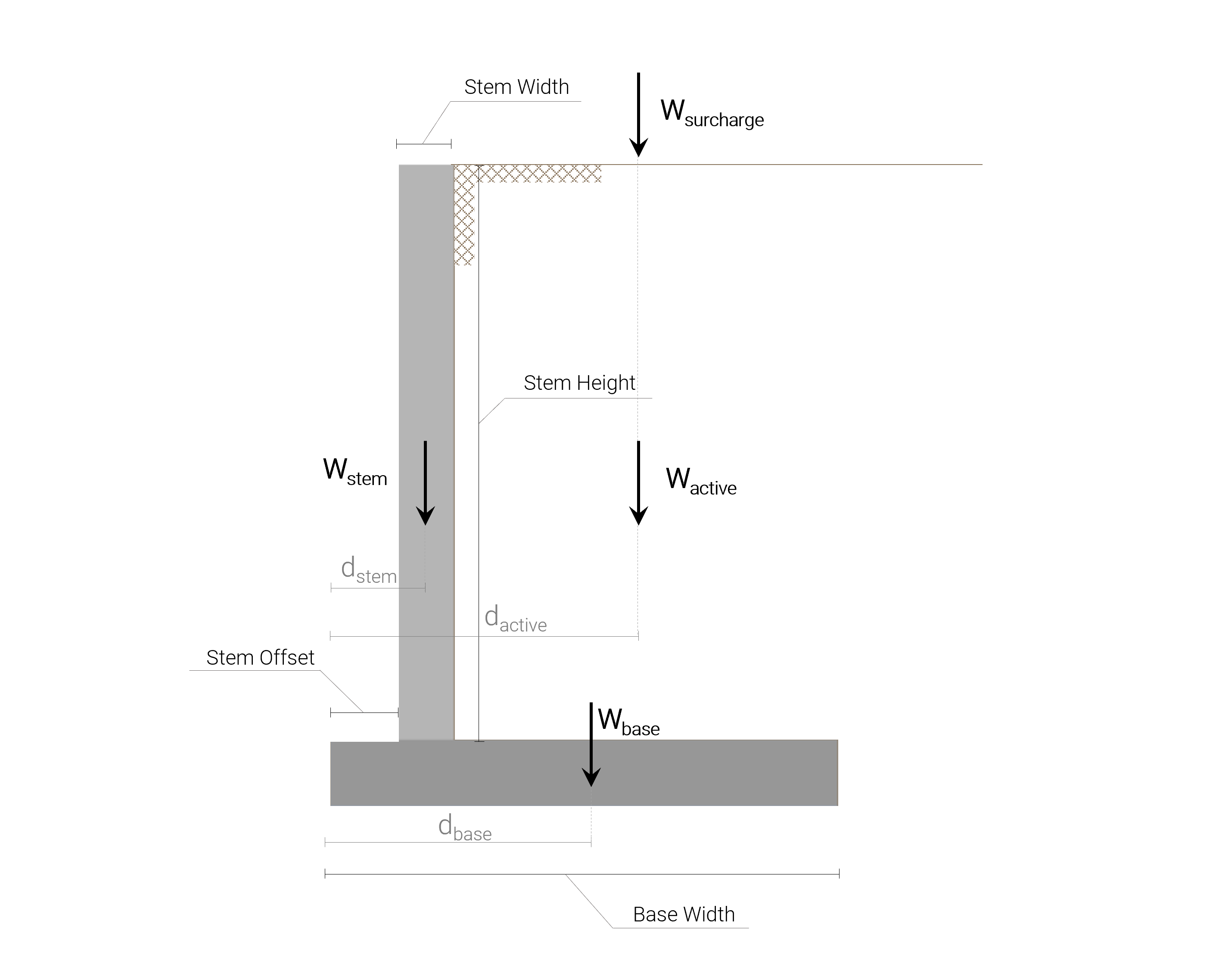
Het is de moeite waard om hier te vermelden, dat het gewicht (verticale belasting) en het moment dat verband houdt met het gedeelte passieve grond wordt verwaarloosd omdat het kan worden verwijderd of geërodeerd en het is een conservatieve aanname.

\(W_{stang} = \gamma_{beton} \cdot (stang_{hoogte} \cdot stam_{breedte} ) = 23.58 \;kN/m^3 \cdot 3.124\;m \cdot 0.305\;[object Window])

\( W_{stang}= 22.467\;kN/m\)

\(W_{baseren} = \gamma_{beton} \cdot (baseren_{dikte} \cdot base_{breedte} ) = 23.58 \;kN/m^3 \cdot 0.381\;m \cdot 2.210\;[object Window])

\( W_{baseren}= 18.855\;kN/m\)

\(W_{actief} = \gamma_{bodem,\;actief} \cdot (stang_{hoogte}\cdot (baseren_{breedte}-stang_{offset}-stang_{breedte}) ) \)

\( W_{actief} = 18.85 \;kN/m^3 \cdot 3.124\;m \cdot (2.210-0.686-0.305)\;[object Window])

\( W_{actief} = 71.784\;kN/m\)

\(W_{toeslag} = toeslag_{toe te passen} \cdot ( (baseren_{breedte}-stang_{offset}-stang_{breedte} ) \)

\( W_{toeslag} = 17.237 \;kN/m \cdot (2.210-0.686-0.305)\;[object Window])

\( W_{toeslag} = 21.012\;kN/m\)

 

Keermuurcalculator

Herstelmoment:

Het herstelmoment is degene die ervoor zorgt dat de muur niet draait ten opzichte van de meest linkerbenedenhoek van de basis. Om het te berekenen, het is vereist om een ​​momentoptelling uit te voeren met betrekking tot het genoemde punt van alle verticale belastingen:

\(M_{stang}=W_{stang}\cdot d_{stang} = 22.467\;kN/m \cdot 0.839\;m=18.839\;kNm/m\)

\(M_{baseren}=W_{baseren}\cdot d_{baseren} = 18.855\;kN/m \cdot 1.105\;m=21.939\;kNm/m\)

\(M_{actief}=W_{actief}\cdot d_{actief} = 71.784\;kN/m \cdot 1.601\;m=114.89\;kNm/m\)

\(M_{toeslag}=W_{toeslag}\cdot d_{toeslag} = 21.012\;kN/m \cdot 1.601\;m=33.630\;kNm/m\)

\( \Sigma{M_{R}} = M_{stang}+M_{baseren}+M_{actief}+M_{toeslag}\)

\( \Sigma{M_{R}} = 18.839+21.939+114.89+33.630\)

\( \Sigma{M_{R}} = 189.298\;kNm/m\)

Horizontale belastingen:

Alle horizontale belastingen waaraan de betonnen vrijdragende keermuur wordt blootgesteld, worden weergegeven in de volgende afbeelding::

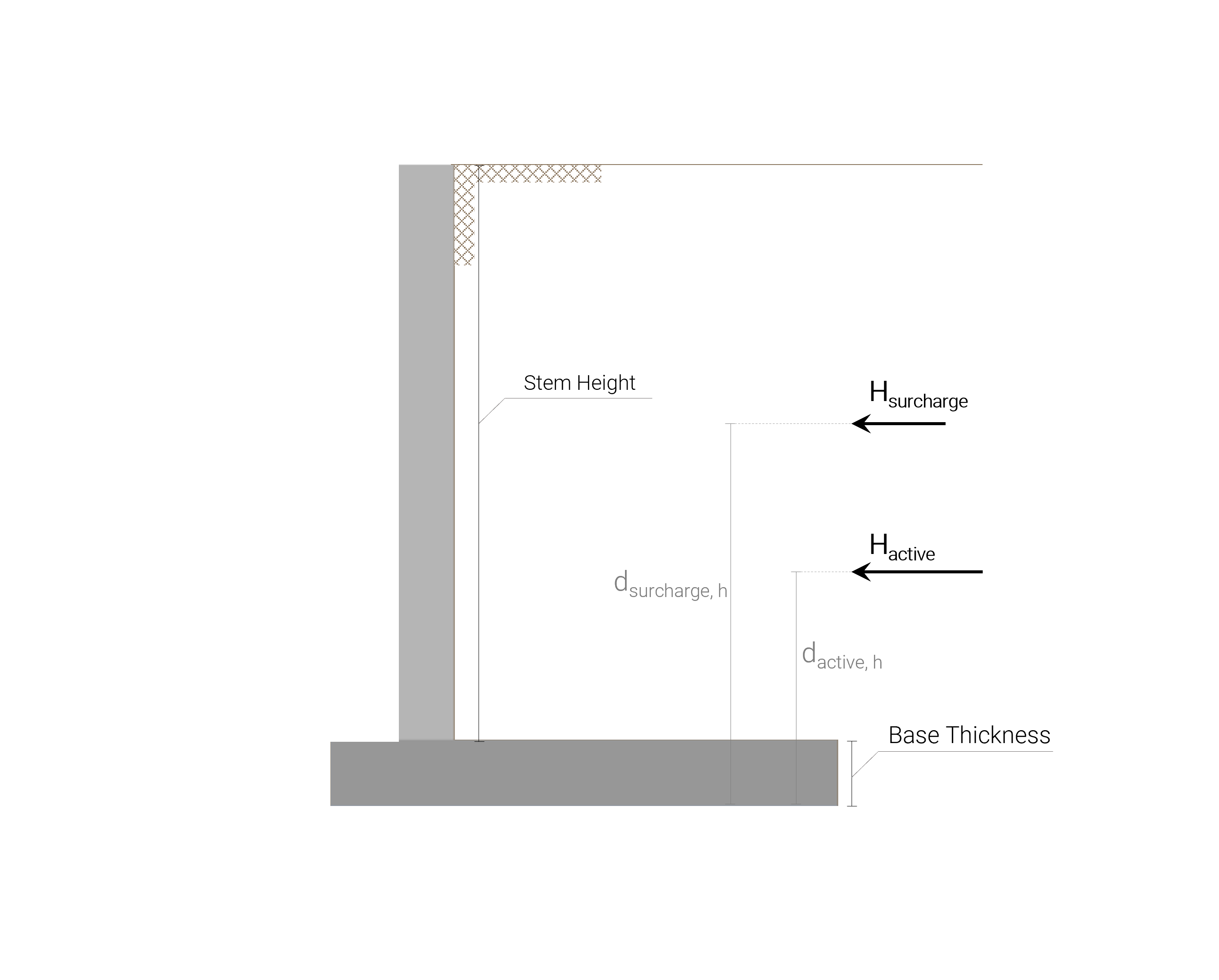
Om de laterale gronddruk te berekenen als gevolg van de vastgehouden actieve bodemdruk en de als gevolg van de toeslag resulterende laterale druk, het is noodzakelijk om de actieve gronddrukcoëfficiënt van Rankine te berekenen:

\( K_a = \frac{1-\zonder(\gamma_{bodem,\;actief})}{1+\zonder(\gamma_{bodem,\;actief})} \)

\( K_a = \frac{1-\zonder(35º)}{1+\zonder(35º)} = 0.271 \)

Met dat resultaat, het is nu mogelijk om de horizontale belasting te berekenen die resulteert uit de laterale actieve druk die de vastgehouden grond uitoefent:

\(H_{actief} = frac{1}{2} \cdot \gamma_{bodem,\;actief} \cdot (stang_{hoogte} + baseren_{dikte})^{2} \cdot K_a \)

\(H_{actief} = frac{1}{2} \cdot 18.85\;kN/m^3 \cdot 3.505^{2} \cdot 0.271 \)

\(H_{actief} = 31.377\;kN / m \)

Voor het berekenen van de horizontale kracht gerelateerd aan de toeslagaanwezigheid, eerst wordt een equivalente bodemhoogte berekend, en dan de werkelijke kracht:

\( h_{bodem,\;gelijk aan} = frac{toeslag_{toe te passen}}{\gamma_{bodem,\;actief}} = frac{17.237 \;= gamma_{2}}{18.85 \;= gamma_{3}} \)

\( h_{bodem,\;gelijk aan} = 0.914 \; m \)

\( H_{toeslag} = \gamma_{bodem,\;actief} \cdot h_{bodem,\;gelijk aan} \cdot (stang_{hoogte} + baseren_{dikte}) \cdot K_a\)

\(H_{toeslag} =\cdot 18.85\;kN/m^3 \cdot 0.914 \; m \cdot 3.505 \; m \cdot 0.271 \)

\(H_{toeslag} = 16.372\;kN / m \)

kantelmoment

Het kantelmoment wordt berekend als het moment dat wordt gegenereerd door de horizontale belastingen ten opzichte van de meest linkerbenedenhoek van de basis. De afstand van de hefboomarm voor elk van de horizontale lasten is::

• Een derde van de hoogte van de muur vanaf de onderkant van de basis voor de resultante van de actieve drukverdeling van de vastgehouden grond. Het is zo, omdat die druk een driehoekige verdeling volgt met een nulwaarde aan de oppervlakte en een maximale waarde aan de onderkant van het basisniveau.
• De helft van de hoogte van de muur vanaf de onderkant van de basis voor het geval van de resulterende horizontale belasting door de aanwezigheid van de meerbelasting. Het is zo omdat die druk een rechthoekige verdeling volgt.

Dat gezegd hebbende, het kantelmoment wordt als volgt berekend::

\( M_{actief} = H_{actief} \cdot \frac{1}{3} \; (stang_{hoogte} + baseren_{dikte}) \)

\( M_{actief} = 31.377\;kN/m \cdot \frac{1}{3} \; 3.505\;m \)

\( M_{actief} = 36.659 \;kNm/m \)

\( M_{toeslag, \;h} = H_{toeslag} \cdot \frac{1}{2} \; (stang_{hoogte} + baseren_{dikte}) \)

\( M_{toeslag, \;h} = 16.372\;kN/m \cdot \frac{1}{2} \; 3.505\;m \)

\( M_{toeslag, \;h} = 28.692\;kNm/m \)

\( \Sigma{M_{OTM}} = M_{actief}+M_{toeslag, \;h}\)

\( \Sigma{M_{OTM}} = 36.659 \;kNm/m+28.692\;kNm/m\)

\( \Sigma{M_{OTM}} = 65.351\;kNm/m\)

Veiligheidsfactor tegen kantelen

ACI 318 beveelt een veiligheidsfactor aan die groter is dan of gelijk is aan: \(2.0\). Het wordt als volgt berekend::

\( FS = \frac{\Sigma{M_{R}}}{\Sigma{M_{OTM}}} \)

\( FS = \frac{189.298\;kN\ast m}{65.351\;kN\ast m}= 2.897 \geven 2.0\) DOORGANG!

 

Keermuurcalculator

In dit artikel, we hebben voorbeelden van berekening van kantelmomenten besproken. SkyCiv biedt een gratis keermuurcalculator die het kantelmoment controleert en een stabiliteitsanalyse uitvoert op uw keermuren. De betaalde versie toont ook de volledige berekeningen, zodat u stap voor stap kunt zien hoe u de stabiliteit van de keermuur tegen kantelen kunt berekenen, glijden en lager!

Keermuurcalculator