Hoe het uiteindelijke draagvermogen van een enkele paal te berekenen

Draagvermogen

---

Het evalueren van het uiteindelijke draagvermogen van een enkele paal is een van de belangrijkste aspecten van het paalontwerp, en kan soms ingewikkeld zijn. Dit artikel bespreekt de geldende vergelijkingen voor het ontwerpen van enkele palen, evenals een voorbeeld.

Het mechanisme voor belastingoverdracht van een enkele stapel gemakkelijk begrijpen, stel je een betonnen paal voor van lengte L met diameter D, zoals te zien in figuur 1.

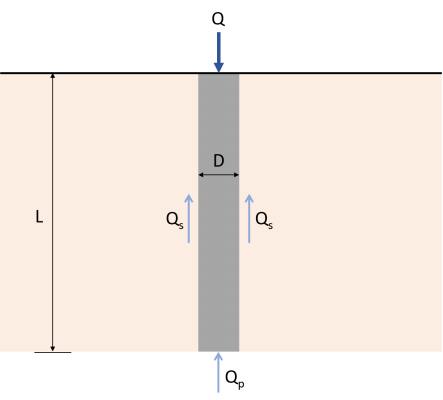
Figuur 1: Lastoverbrengingsmechanisme voor palen

De belasting Q die op de paal wordt uitgeoefend, wordt rechtstreeks overgebracht op de grond aan de onderkant van de paal. Een deel van deze belasting zal worden weerstaan ​​door de zijkanten van de paal met behulp van iets genaamd “huid wrijving” ontwikkeld langs de schacht (Q_s), en de rest zal worden weerstaan ​​door de grond waarop de paal rust (Q_p). Daarom, het ultieme draagvermogen (Qu) van een stapel zal worden gegeven door de vergelijking (1). Er zijn meerdere methoden beschikbaar om de waarden van Q te schatten_p en Q_s.

\( {Q}_{u} = {Q}_{p} + {Q}_{s} \) (1)

Q_u = Ultiem draagvermogen

Q_p = Draagvermogen van het uiteinde

Q_s = Huidwrijvingsweerstand

Wil je de Foundation Design-software van SkyCiv proberen?? Met onze gratis tool kunnen gebruikers lastdragende berekeningen uitvoeren zonder download of installatie!

Stichting ontwerp rekenmachine

Einddragende capaciteit, Q_p

---

Het uiteindelijke draagvermogen aan het uiteinde is theoretisch de maximale belasting per oppervlakte-eenheid die kan worden gedragen door de grond in het dragen, zonder falen. De volgende vergelijking van Karl Von Terzaghi, de vader van de grondmechanica, is een van de eerste en meest gebruikte theorie bij het evalueren van het uiteindelijke draagvermogen van funderingen. Terzaghi's vergelijking voor het uiteindelijke draagvermogen kan worden uitgedrukt als:

\( {q}_{u} = (c × {N}_{c}) + (q × {N}_{q}) + (\frac{1}{2} × γ × B × {N}_{c}) \) (2)

q_u = Ultieme einddragende capaciteit

c = Samenhang van de bodem

q = Effectieve bodemdruk

γ = Gewicht per stuk grond

B = Doorsnedediepte of diameter

N_c, N_q, N_c = Dragende factoren

Sinds q_u is in termen van belasting per oppervlakte-eenheid of druk, vermenigvuldiging met de oppervlakte van de dwarsdoorsnede van de paal resulteert in het draagvermogen van het uiteinde (Q_p) van de stapel. De resulterende waarde van de laatste term van Vergelijking 2 is verwaarloosbaar vanwege een relatief kleine poolbreedte, Vandaar, het kan uit de vergelijking worden verwijderd. Dus, het uiteindelijke einddragende draagvermogen van de paal kan worden uitgedrukt zoals weergegeven in de vergelijking (3). Deze aangepaste versie van de vergelijking van Terzaghi wordt gebruikt in de SkyCiv Foundation-module bij het ontwerpen van palen.

\( {Q}_{p} = {A}_{p} × [(c × {N}_{c}) + (q × {N}_{q}) ] \) (3)

A_p = Doorsnede van de paal

Dragende factoren N_c en N_q zijn niet-dimensionaal, empirisch afgeleid, en zijn functies van de bodemwrijvingshoek (Phi). Onderzoekers hebben de berekeningen die nodig zijn om de dragende factoren te vinden, al voltooid. Tafel 1 vat de waarden van N samen_q volgens Naval Facilities Engineering Command (NAVFAC DM 7.2, 1984). De waarde van N_c is ongeveer gelijk aan 9 voor stapels onder kleiachtige bodems.

Dragende factor (Nq)
Wrijvingshoek (O)	26	28	30	31	32	33	34	35	36	37	38	39	40
Gedreven stapels	10	15	21	24	29	35	42	50	62	77	86	120	145
Verveelde stapels	5	8	10	12	14	17	21	25	30	38	43	60	72

Tafel 1: N_q waarden van NAVFAC DM 7.2

Weerstandsvermogen tegen huidwrijving, Q_s

---

Huidwrijvingsweerstand van palen wordt ontwikkeld langs de lengte van de paal. Over het algemeen, de wrijvingsweerstand van een paal wordt uitgedrukt als:

\( {Q}_{s} = ∑ (p × ΔL × f) \) (4)

p = Omtrek van de paal

ΔL = incrementele poollengte waarover p en f worden genomen

f = Wrijvingsweerstand van de unit op elke diepte

De waarde van de wrijvingsweerstand van de eenheid schatten (f) vereist een aantal belangrijke factoren om rekening mee te houden, zoals de aard van de paalinstallatie en de bodemclassificatie. Vergelijkingen (5) en (6) toont de computationele methode om de eenheid van wrijvingsweerstand van palen in zand- en kleiachtige bodems te vinden, respectievelijk. Tabellen 2 en 3 presenteer de aanbevolen effectieve gronddrukcoëfficiënt (K) en de wrijvingshoek van de grondpaal (δ ’), volgens NAVFAC DM7.2.

Voor zandgronden:

\( f = K × σ ’× tan(δ ’) \) (5)

K = Effectieve gronddrukcoëfficiënt

σ’ = Effectieve verticale spanning op de betreffende diepte

d’ = Wrijvingshoek grond-paal

Voor kleiachtige bodems:

\( f = α × c \) (6)

α = empirische adhesiefactor

Wrijvingshoek van grond-stapel (δ ’)
Stapel Type	d’
Stalen stapel	20º
Houten stapel	3/4 × Φ
Betonnen stapel	3/4 × Φ

Tafel 2: Wrijvingshoekwaarden grond-stapel (NAVFAC DM7.2, 1984)

Laterale aardingsdrukcoëfficiënt (K)
Stapel Type	Compressie stapel	Spanningsstapel
Gedreven H-palen	0.5-1.0	0.3-0.5
Aangedreven verplaatsingspalen (ronde, rechthoekig)	1.0-1.5	0.6-1.0
Aangedreven verplaatsingspalen (taps toelopend)	1.5-2.0	1.0-1.3
Aangedreven gespoten palen	0.4-0.9	0.3-0.6
Verveelde stapels (<24″ Diameter)	0.7	0.4

Tafel 3: Laterale aardingsdrukcoëfficiënt (K) Waarden (NAVFAC DM7.2, 1984)

Hechtingsfactor (een)
c / peen	een
≤ 0.1	1.00
0.2	0.92
0.3	0.82
0.4	0.74
0.6	0.62
0.8	0.54
1.0	0.48
1.2	0.42
1.4	0.40
1.6	0.38
1.8	0.36
2.0	0.35
2.4	0.34
2.8	0.34

Notitie: p_een = atmosferische druk ≈ 100 kN / m²

Tafel 4: Adhesiefactorwaarden (Terzaghi, Pikken, en Mesri, 1996)

Voorbeeld: Berekening van de capaciteit van palen in zand

---

Een betonnen paal van 12 meter lang met een diameter van 500 mm wordt in meerdere zandlagen gedreven zonder dat er grondwater aanwezig is. Vind het ultieme draagvermogen (Q_u) van de stapel.

Details
Sectie
Diameter	500 mm
Lengte	12 m
Laag 1-bodemeigenschappen
Dikte	5 m
Gewichtseenheid	17.3 kN / m3
Wrijvingshoek	30 Graden
Samenhang	0 kPa
Grondwatertabel	Niet aanwezig
Laag 2-bodemeigenschappen
Dikte	7 m
Gewichtseenheid	16.9 kN / m3
Wrijvingshoek	32 Graden
Samenhang	0 kPa
Grondwatertabel	Niet aanwezig

Stap 1: Bereken het draagvermogen van het uiteinde (Q_p).

Aan het uiteinde van de stapel:

A_p = (π / 4) × D² = (π / 4) × 0.5²

A_p = 0.196 m²

c = 0 kPa

θ = 32º

N_q = 29 (Van tafel 1)

Effectieve bodemdruk (q):

q = (c₁ × t₁) + (c₂ × t₂) = (5 m × 17.3 kN / m³) + (7 m × 16.9 kN / m³)

q = 204.8 kPa

Gebruik dan vergelijking (3) voor het draagvermogen van het uiteinde:

Q_p = A_p × [(c × N_c) + (q × N_q)]

Q_p = 0.196 m² × ( 204.8 KPa × 29)

Q_p = 1,164.083 kN

Stap 2: Bereken de huidwrijvingsweerstand (Q_s).

Vergelijkingen gebruiken (4) en (5), bereken de huidwrijving per bodemlaag.

Q_s = ∑ (p × ΔL × f)

p = π × D = π × 0.5 m

p = 1.571 m

Laag 1:

ΔL = 5 m

f₁ = K × σ’₁× bruin(δ ’)

K = 1.25 (Tafel 3)

d’ = 3/4 × 30º

d’ = 22.50º

σ’₁ = γ₁ × (0.5 × t₁) = 17.3 kN / m³ × (0.5 × 5 m)

σ’₁ = 43.25 kN / m²

f₁ = 1.25 × 43.25 kN / m² × bruin(22.50º)

f₁ = 22.393 kN / m²

Q_s1 = p × ΔL × f₁ = 1.571 m × 5 m × 22.393 kN / m²

Q_s1 = 175.897 kN

Laag 2:

ΔL = 7 m

f₂ = K × σ’₂× bruin(δ ’)

K = 1.25 (Tafel 3)

d’ = 3/4 × 32º

d’ = 24º

σ’₂ = (c₁ × t₁) + [c₂ × (0.5 × t₂)] = (17.3 kN / m³ × 5 m) + [16.9 kN / m³ ×(0.5 × 7 m)]

σ’₂ = 145.65 kN / m²

f₂ = 1.25 × 145.65 kN / m² × bruin(24º)

f₂ = 81.059 kN / m²

Q_S2 = p × ΔL × f₂ = 1.571 m × 7 m × 81.059 kN / m²

Q_S2 = 891.406 kN

Totale weerstand tegen huidwrijving:

Q_s = Q_s1+ Q_S2 = 175.897 kN + 891.406 kN

Q_s = 1,067.303 kN

Stap 3: Bereken voor het ultieme draagvermogen (Q_u).

Q_u = Q_p+ Q_s = 1,164.083 kN + 1,067.303 kN

Q_u = 2,231.386 kN

Voorbeeld 2: Berekening van de capaciteit van palen in klei

---

Overweeg een 406 mm diameter betonnen paal met een lengte van 30m ingebed in gelaagd, verzadigde klei. Vind het ultieme draagvermogen (Q_u) van de stapel.

Details
Sectie
Diameter	406 mm
Lengte	30 m
Laag 1-bodemeigenschappen
Dikte	10 m
Gewichtseenheid	8 kN / m3
Wrijvingshoek	0º
Samenhang	30 kPa
Grondwatertabel	5 m
Laag 2-bodemeigenschappen
Dikte	10 m
Gewichtseenheid	19.6 kN / m3
Wrijvingshoek	0º
Samenhang	0 kPa
Grondwatertabel	Volledig ondergedompeld

Stap 1: Bereken het draagvermogen van het uiteinde (Q_p).

Aan het uiteinde van de stapel:

A_p = (π / 4) × D²= (π / 4) × 0.406²

A_p = 0.129 m²

c = 100 kPa

N_c = 9 (Typische waarde voor klei)

Q_p = (c × N_c) × A_p = (100 kPa × 9) × 0.129 m²

Q_p = 116.1 kN

Stap 2: Bereken de huidwrijvingsweerstand (Q_s).

Vergelijkingen gebruiken (4) en (6), bereken de huidwrijving per bodemlaag.

Q_s = ∑ (p × ΔL × f)

p = π × D = π × 0.406 m

p = 1.275 m

Laag 1:

ΔL = 10 m

een₁ = 0.82 (Tafel 4)

c₁ = 30 kPa

f₁= α₁ × c₁ = 0.82 × 30 kPa

f₁ = 24.6 kN / m²

Q_s1 = p × ΔL × f₁ = 1.275 m × 10 m × 24.6 kN / m²

Q_s1 = 313.65 kN / m²

Laag 2:

ΔL = 20 m

een₂= 0.48 (Tafel 4)

c₂ = 100 kPa

f₂ = α₂ × c₂ = 0.48 × 100 kPa

f₂ = 48 kN / m²

Q_S2 = p × ΔL × f₂ = 1.275 m × 20 m × 48 kN / m²

Q_S2 = 1,224 kN / m²

Totale weerstand tegen huidwrijving:

Q_s = Q_s1+ Q_S2 = 313.65 kN + 1224 kN

Q_s = 1,537.65 kN

Stap 3: Bereken voor het ultieme draagvermogen (Q_u).

Q_u = Q_p+ Q_s = 116.1 kN + 1537.65 kN

Q_u = 1,653.75 kN

Wil je de Foundation Design-software van SkyCiv proberen?? Met onze gratis tool kunnen gebruikers lastdragende berekeningen uitvoeren zonder download of installatie!

Stichting ontwerp rekenmachine

Referenties:

• De, B.M. (2007). Principes van funderingstechniek (7e editie). Wereldwijde engineering
• Rajapakse, R. (2016). Stapelontwerp en constructie Vuistregel (2e editie). Elsevier Inc..
• Tomlinson, M.J. (2004). Paalontwerp en bouwpraktijk (4e editie). E & FN Spon.