Een walkthrough van de berekeningen om een geïsoleerde fundering te ontwerpen (ALS 3600 2018)
De fundering is een essentieel bouwsysteem dat kolom- en muurkrachten overbrengt op de ondersteunende grond. Afhankelijk van de bodemeigenschappen en de gebouwbelasting kan de ingenieur kiezen voor een ondiep of diep funderingssysteem.
SkyCiv FoundationDesign-module omvat het analyseren en ontwerpen van geïsoleerde voetstukken die voldoen aan de Australische normen (ALS 3600 2009 & 2018).
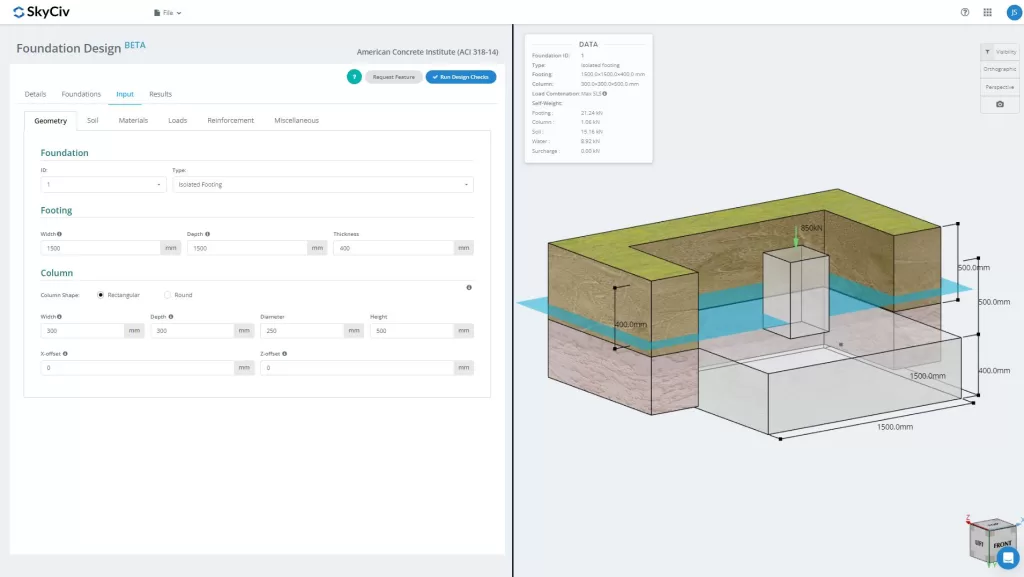
Wil je de Foundation Design-software van SkyCiv proberen?? Met onze tool kunnen gebruikers lastberekeningen uitvoeren zonder enige download of installatie!
Ontwerp van een geïsoleerde fundering
Dimensievereisten:
Om de afmetingen van een geïsoleerde voet te bepalen, service of niet-gefactureerde belastingen, zoals permanente actie (G), opgelegde actie (Q), windactie (Wu), aardbeving actie (Eu), en Su wordt toegepast met behulp van belastingscombinaties, zoals gedefinieerd door AS 3600. Welke belastingcombinatie ook van toepassing is, wordt beschouwd als de ontwerpbelasting, en wordt vergeleken met de toegestane bodemdruk zoals weergegeven in vergelijking 1.
\(\tekst{q}_{\tekst{een}} = frac{\tekst{P.}_{\tekst{n}}}{\tekst{A}} \rechter pijl \) Vergelijking 1
qeen = toelaatbare bodemdruk
P.n = serviceniveau ontwerpbelastingen
A = funderingsoppervlak
De afmetingen van de fundering kunnen in eerste instantie worden geschat door het funderingsoppervlak op te lossen (A) met behulp van vergelijking 1.
\(\tekst{A} = frac{\tekst{P.}_{\tekst{n}}}{\tekst{q}_{\tekst{een}}} \rechter pijl \) Vergelijking 1a
Eenrichtingsschaar
De eenrichtingsschaar grenstoestand:, ook gekend als buigschaar, erkent dat de fundering kan bezwijken bij afschuiving, vergelijkbaar met een brede balk langs een kritisch afschuifvlak dat zich op een afstand bevindt “d” vanaf de voorkant van de kolom (Figuur 1), te krijgen op basis van AS3600-clausule 8.2.7.1
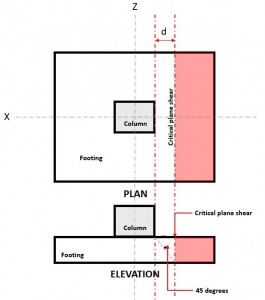
Figuur 1. Kritisch schuifvlak van eenrichtingsschuif
De Een manier Schuintrekken Vraag naar of V u wordt berekend in de veronderstelling dat de voet vrijdragend is, weg van de kolom waar het rode gebied is aangegeven in de figuur 1.
De Een manier Schuintrekken Capaciteit of ϕVuc wordt gedefinieerd als de ultieme schuifsterkte en berekend met behulp van vergelijking 2 per AS3600-09 Kl 8.2.7.1.
\( \phi tekst{V }_{uc} = phi beta_{1} \maal bèta_{2} \maal bèta_{3} \maal b_{v} \keer d_{De} \keer f_{CV} \keren per_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak}^{\frac{2}{3}} \rechter pijl \) Vergelijking 2 (AS3600 Vgl. 8.2.7.1)
ϕ = ontwerpfactor voor afschuiving
b1= 1.1(1.6 – dDe/1000) 1.1 of 1.1(1.6(1-dDe/1000) 0.8
b2 = 1, voor leden die onderhevig zijn aan pure buiging; of
=1-(N*/3.5Ag) 0 voor staaf onderworpen aan axiale spanning; of
=1-(N*/14Ag) voor leden die onderhevig zijn aan axiale compressie
b3 = 1, of kan worden opgevat als –
2dDe/eenv maar niet groter dan 2
eenv = afstand voor het gedeelte waarop afschuiving wordt beschouwd tot het vlak van de dichtstbijzijnde steunpunt
fCV = f’c1/3 ≤ 4 MPa
Ade opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak = dwarsdoorsnedeoppervlak van langswapening
Afschuifvraag en afschuifcapaciteit moeten aan de volgende vergelijking voldoen om aan de ontwerpvereisten van AS te voldoen 3600-09:
\(\tekst{V }_{\tekst{u}} \lees phitext{V }_{\tekst{uc}} \rechter pijl \) Vergelijking 3 (per AS3600 Kl. 8.2.5)
SkyCiv Foundation, in overeenstemming met vergelijking 3, berekent de eenzijdige afschuivingsnutratio (Vergelijking 4) door de afschuifvraag te nemen boven de afschuifcapaciteit.
\( \tekst{Nutsverhouding:} = frac{\tekst{Vraag naar schuifkracht}}{\tekst{Afschuifcapaciteit:}} \rechter pijl \) Vergelijking 4
Tweerichtingsschaar
De Tweerichtingsschaar grenstoestand:, ook gekend als ponsschaar, breidt zijn kritieke gedeelte uit tot een afstand “d/2” vanaf de voorkant van de kolom en rond de omtrek van de kolom (Figuur 2) te krijgen op basis van AS3600-clausule 9.2.3(een).
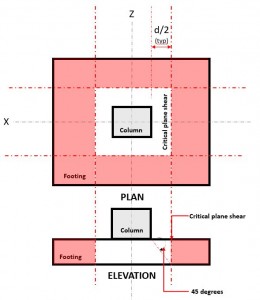
Figuur 2. Kritisch afschuifvlak van bidirectionele afschuiving:
De Twee manierenhoor vraag of V u vindt plaats in het kritische afschuifvlak, gelegen op een afstand van “d/2” waar de (rood) gearceerd gebied, zoals aangegeven in figuur 2.
De Tweerichtingsverkeer Afschuifcapaciteit: of Vuo wordt gedefinieerd als de ultieme schuifsterkte en berekend met behulp van vergelijking 5 te krijgen op basis van AS3600-clausule 9.2.3
\( \phi V_{uo} = phi tijden u tijden f_{CV} \maal d pijl naar rechts \) Vergelijking 5 (AS3600 Kl. 9.2.3(een))
fCV = 0.17(1 + 2/bh) √f’c ≤ 0,34√f’c
bh = verhouding van de lengte van de kolom op de Z-as over de X-as
d = afstand van extreme compressievezel tot zwaartepunt van longitudinale trekwapening (mm)
u = lengte van de kritische afschuifomtrek (mm)
Afschuifvraag en afschuifcapaciteit moeten aan de volgende vergelijking voldoen om aan de ontwerpvereisten van AS te voldoen 3600:
\(\tekst{V }_{\tekst{u}} \lees phitext{V }_{\tekst{uo}} \rechter pijl \) Vergelijking 6 (per AS3600 Kl. 8.2.5)
SkyCiv Foundation, in overeenstemming met vergelijking 6, berekent de tweezijdige afschuivingsnutratio (Vergelijking 7) door de afschuifvraag te nemen boven de afschuifcapaciteit.
\( \tekst{Nutsverhouding:} = frac{\tekst{Vraag naar schuifkracht}}{\tekst{Afschuifcapaciteit:}} \rechter pijl \) Vergelijking 7
Buiging
Op geïsoleerde voet, de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak. Buigmomenten worden in elke richting op sectie berekend 0.7eensup afstand vanaf het midden van de kolom, waar eensup de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak.
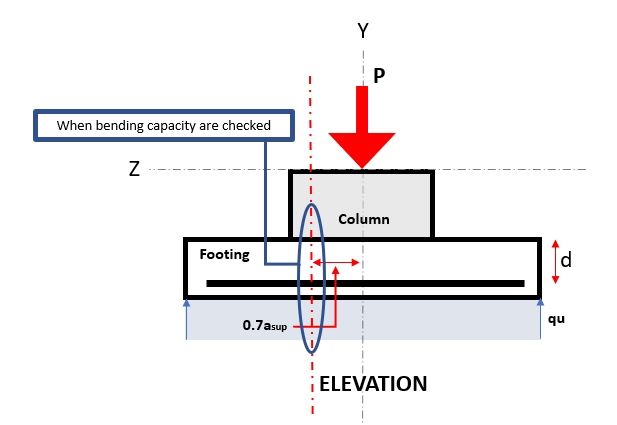
Figuur 3. Kritische buigingssectie
De buigzaam grenstoestand treedt op bij de kritische buigsectie, gelegen 0.7eensup vanaf het midden van de voet (Zie afbeelding 3).
De Buigvraag of Mu bevindt zich op het kritieke buiggedeelte zoals aangegeven in de afbeelding 3, en wordt berekend met behulp van vergelijking 8.
\( \tekst{M}^{*}= q_{u} \keer D_{f} \keer links( \frac{ \frac{b_{f} – b_{c}}{2} }{2} \Rechtsaf)^{2} \rechter pijl \) Vergelijking 8
De Buigvermogen of Mn wordt berekend met behulp van vergelijking 9.
\(M_{n} = A_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak} \keer f_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak} \maal d maal left(1- \frac{0.5}{\alfa_{s}} \[object Window]{EEN_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak} \keer f_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak}}{b tijden d tijden f’_{c}} \Rechtsaf) \rechter pijl \) Vergelijking 9
ϕ = buigingsontwerpfactor
b = voetafmeting evenwijdige x-as, (mm)
d = afstand van extreme compressievezel tot zwaartepunt van longitudinale trekwapening, (mm)
Ade opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak = versterkingsgebied, (mm2)
a = diepte van equivalent rechthoekig spanningsblok, (mm)
fsy = wapeningssterkte, (MPa)
Momentvraag en Momentcapaciteit moeten aan de volgende vergelijking voldoen om aan de ontwerpvereisten van AS te voldoen 3600:
\(\tekst{M}_{\tekst{u}} \lees phitext{M}_{\tekst{n}} \rechter pijl \) Vergelijking 10 (per AS3600 Kl. 8.2.5)
SkyCiv Foundation, in overeenstemming met vergelijking 10, berekent de buigutiliteitsratio (Vergelijking 11) door de buigvraag te nemen boven de buigcapaciteit.
\( \tekst{Nutsverhouding:} = frac{\tekst{Flexure-vraag}}{\tekst{Buigcapaciteit:}} \rechter pijl \) Vergelijking 11
de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak
De benodigde hoeveelheid wapening wordt bepaald door de eisen aan de buigsterkte, de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak. 21.3.1 (b)
\( \de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak{ \tekst{min} } = 0.19 \[object Window]{D}{d}^{2} \[object Window]{f'_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak} }{ f_{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak} } \rechter pijl \) Vergelijking 12
Het oppervlak van staal kan worden bepaald met de volgende vergelijking:
\( \[object Window]{ 2.7 \de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak{*} }{ d ^{2} } \tekst{ of } \tekst{A}_{\tekst{de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak}} = frac{ \tekst{M}^{*} }{ 370 \keer tekst{d} } \rechter pijl \) Vergelijking 13
de opwaartse bodemdruk veroorzaakt bidirectionele buiging met trekspanningen aan het bodemoppervlak 3600, een minimale betondekking van 60 mm voor houvast wordt aanbevolen.
Aanvullende verificaties
Andere verificaties die niet in de code worden vermeld, inclusief bodemdrukcontroles, verheffen, en andere stabiliteitscontroles worden ook geverifieerd.
Bodemdruk
De bepaling van de basisdruk of de interactie tussen de grond en de fundering is voornamelijk afhankelijk van de afmetingen van de fundering en de daaruit voortvloeiende excentriciteit van de uitgeoefende belastingen.. Afhankelijk van de positionering van deze resulterende excentriciteit, de basisdruk kan volledige of gedeeltelijke compressie van de voet veroorzaken. Met deze beoordeling kunnen we bevestigen of de onderliggende grond het geheel van de belastingen die vanaf de fundering worden overgedragen, kan dragen.
Voor een gedetailleerde handleiding voor het handmatig berekenen van de bodemdruk, Raadpleeg deze link: Drukverdeling onder een rechthoekige betonnen voet
De utiliteitsratio wordt geëvalueerd door de maximale bodemdruk te vergelijken (staat van bruikbaarheid) met het toegestane bruto draagvermogen van de bodem:
\( \tekst{Nutsverhouding:} = frac{\tekst{Max. Hoogte. Bodemdruk}}{\tekst{Bruto toelaatbaar bodemdraagvermogen}} \rechter pijl \) Vergelijking 14
Hieronder volgen de verschillende manieren om de gronddrukcoëfficiënten te bepalen om de eenheidswrijvingsweerstand van palen in zand te berekenen
Controleert de heersende axiale belasting die op de fundering inwerkt. Telt alle verticale belastingen op, inclusief de gebruikersbelasting en eigen gewichten van de kolom, voetplaat, bodem, en drijvende kracht. Als de kolom een opwaartse kracht ervaart, de opgegeven eigengewichten moeten de opwaartse kracht compenseren; anders-, het ontwerp riskeert te mislukken als gevolg van instabiliteit.
Met de laatste knop in het menu aan de linkerkant kunt u de waarde van de toeslag wijzigen
Het kantelen van de voet wordt gecontroleerd door alle momenten rond een punt in de voet op te tellen, inclusief alle krachten die erop inwerken.. Alle bruikbaarheidsbelastingcombinaties moeten in aanmerking worden genomen om het geldende kantelmoment te controleren. Meestal, een veiligheidsfactor van 1.5-2 wordt gebruikt om te evalueren of de voet de kantelcontrole doorstaat.
Met de laatste knop in het menu aan de linkerkant kunt u de waarde van de toeslag wijzigen
Om te controleren op glijden, de som van de horizontale weerstandsbelastingen die naar rechts wijzen, wordt gedeeld door de som van de naar links wijzende belastingen.
- Weerstand tegen belastingen:
- Horizontale kracht door wrijving tussen de voetplaat en de ondergrond van de onderbouw
- Passieve bodemdruk (indien inbegrepen)
- Glijdende lasten:
- De horizontale component van de actieve bodemdruk
- De horizontale component van de resulterende druk van de toeslag
Over het algemeen, een minimale veiligheidsfactor van 1.5 is gebruikt. Als er geen horizontale kracht op de voet inwerkt, controleren op glijden is niet vereist.
SkyCiv Foundation-ontwerpmodule
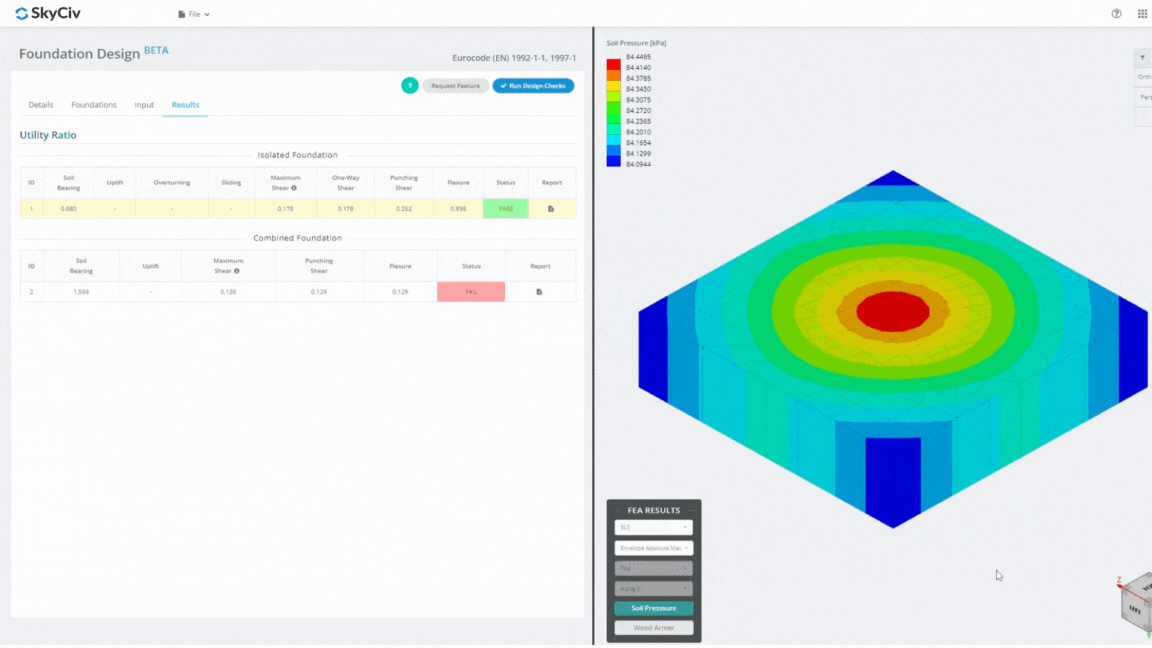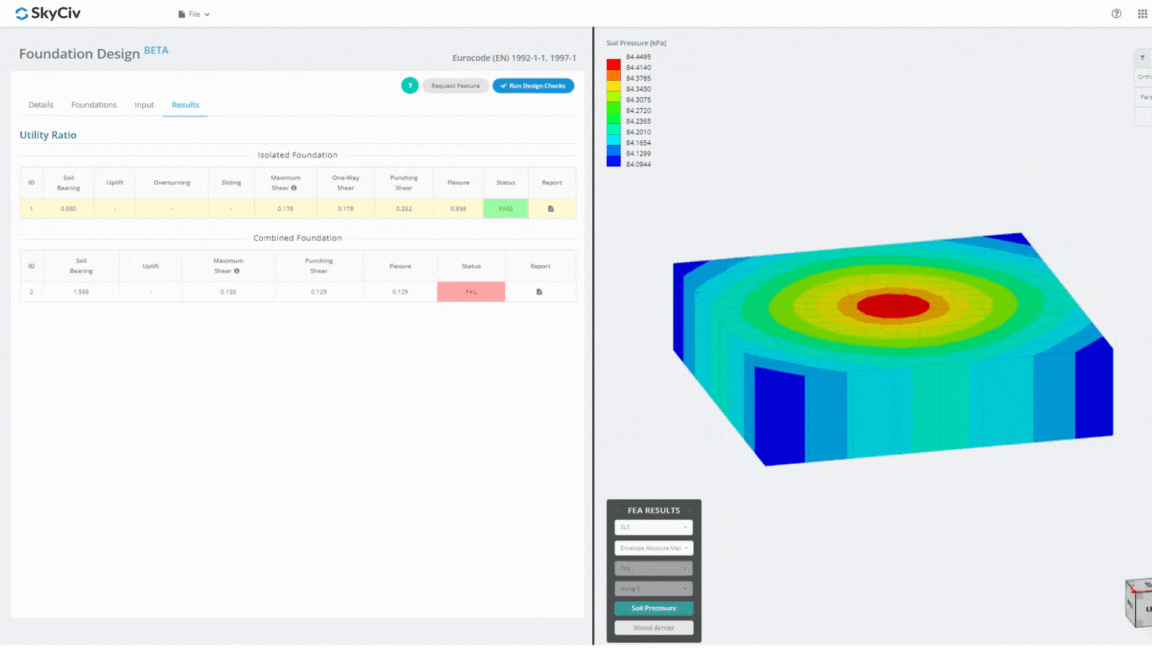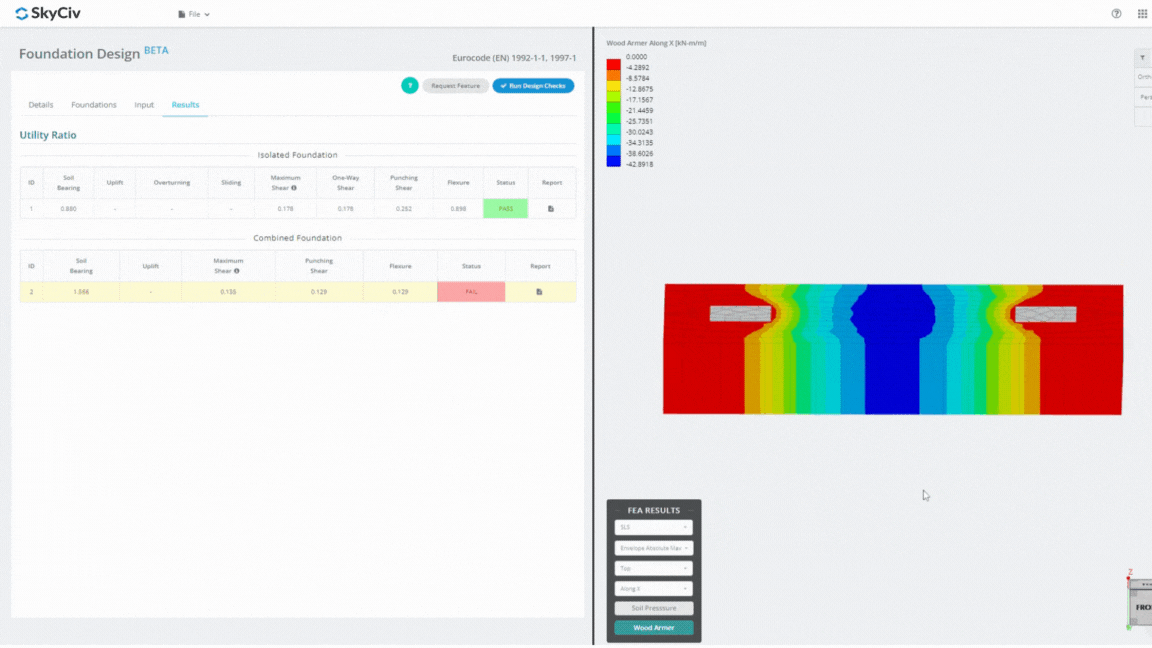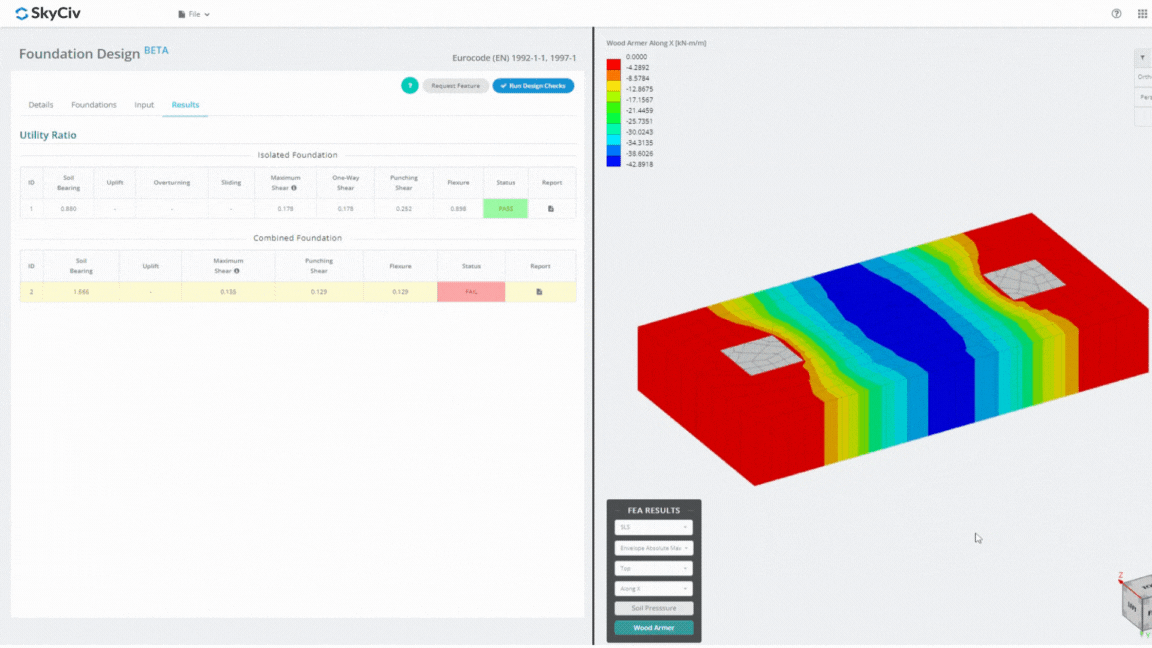
De Foundation Design Module is een krachtig hulpmiddel dat is geïntegreerd met Eindige Elementenanalyse (LELIJK), in staat om grondige bodemdruk- en houtbewapeningsanalyses uit te voeren voor gedetailleerde buigcontroles. Het voert alle door ACI gespecificeerde structurele controles uit 318 en andere hierboven genoemde verificaties en presenteert deze in een uitgebreid rapport.
Aan de slag met SkyCiv Foundation vandaag!
Lanceer de Stichting ontwerp en probeer het vandaag nog! Het is gemakkelijk om aan de slag te gaan, maar als u meer hulp nodig heeft, bezoek dan zeker onze documentatie of neem contact met ons op!
Geen SkyCiv-gebruiker? Schrijf je in voor een gratis 14 Dag op proef starten!
Productontwikkelaar
BSc (Civiel), MSc (Civiel)
Albert Pamonag
Bouwkundig ingenieur, Product ontwikkeling
B.S. Civiele techniek
Referenties
- Raad van Normen Australië. (2009) Australische standaard AS3600-2009.
- SJ Foster, AE Kilpatrick & RF-waarschuwing. (2011) Basisprincipes van gewapend beton 2e editie.
- Taylor, Andrew, et al. Het handboek voor het ontwerpen van gewapend beton: een aanvulling op ACI-318-14. Amerikaans Betoninstituut, 2015.
- YC Loo & SH Chowdhury. (2013) Versterkt & Voorgespannen beton.




