Hoe axiale krachten van een truss-systeem te berekenen met behulp van de verbindingsmethode?
In deze tutorial, we zullen uitleggen hoe we de verbindingsmethode kunnen gebruiken om de interne staafkrachten in een truss-systeem of constructie te berekenen.
Deze krachten staan bekend als axiale krachten en zijn erg belangrijk bij truss-analyse. Als u niet zeker weet wat een truss wordt gezien in ons artikel – Wat is een truss. De methode van gewrichten houdt in feite in dat naar elk van de 'gewrichten wordt gekeken’ (waar de leden elkaar ontmoeten) en het toepassen van statische vergelijkingen om op te lossen.
Het mooie is, SkyCiv Truss doet dit automatisch voor je. Modelleer uw eigen spanten en de software laat u stap voor stap de methode van verbindingen zien!
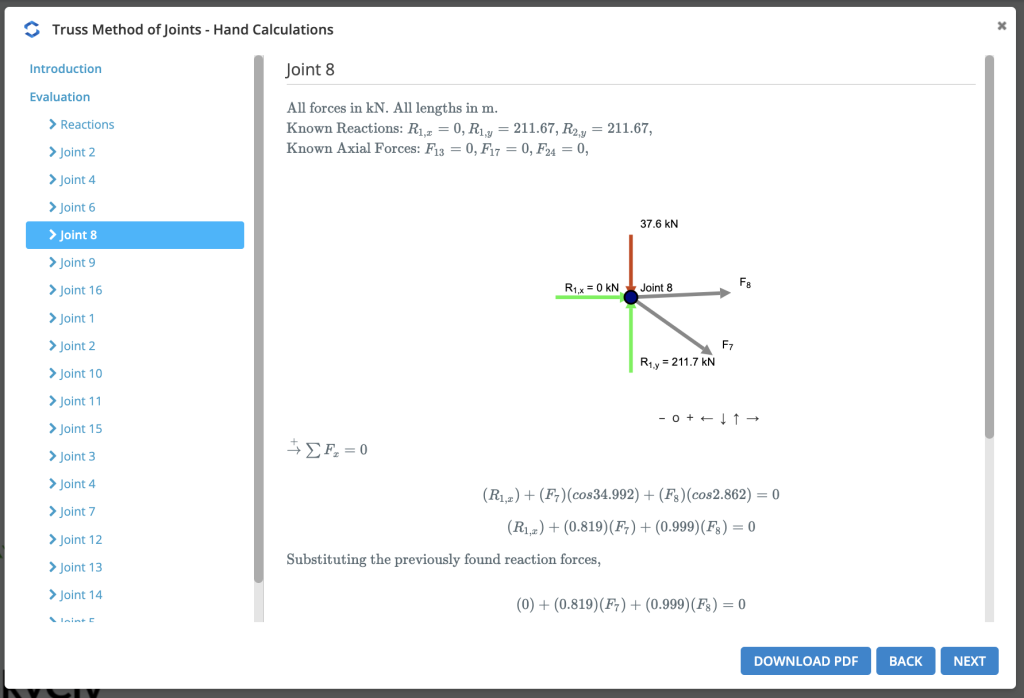
Stap 1: Bereken de reacties bij de steunen
Eerste, we berekenen de reacties bij de steunen. We beginnen met het bekijken van een eenvoudig voorbeeld van een 5 lid truss-systeem:
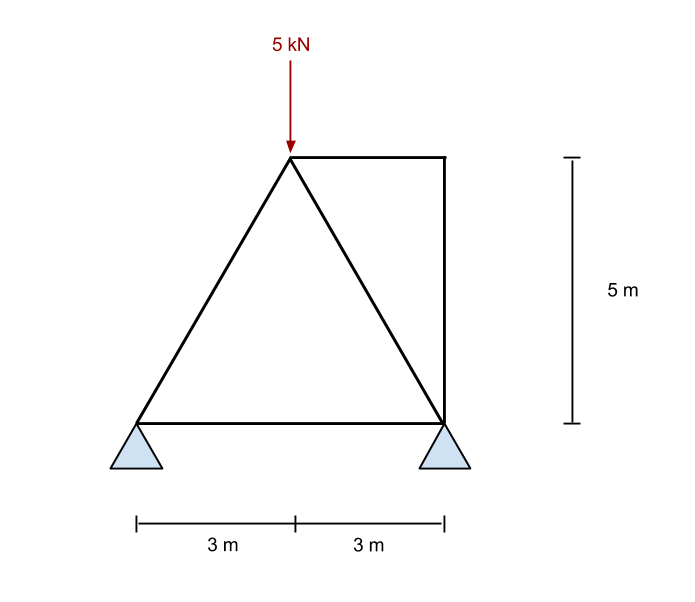
Om de te berekenen buigmoment in dit truss-systeem, we nemen eerst de som van de momenten bij de linker reactie als nul. Dit doen we door alle leden te negeren en alleen naar de krachten en steunen in de constructie te kijken. Dit is hetzelfde als de methode die werd gebruikt in de buigmomentreacties in onze vorige tutorial.
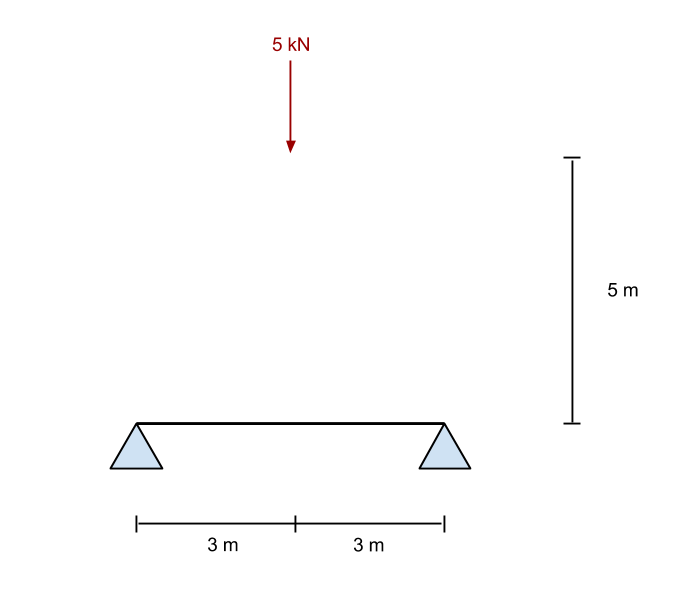
Uit de bovenstaande vergelijkingen, we lossen de reactiekracht op bij punt B (de juiste ondersteuning). In ons voorbeeld, dit blijkt te zijn 2.5 kN in opwaartse richting. Nu, als we de som van de krachten in de y nemen (verticaal) richting, we vinden dat ondersteuning A (de linker steun) wordt ook gegeven als 2.5 kN.
Stap 2: Overweeg een van de ondersteuningen:
Nu we de reactiekrachten hebben, kunnen we beginnen met de analyse van de rest van deze truss-structuur. Ten eerste, we kijken naar een van onze bekende krachten – in dit geval, we zullen de linker ondersteuningsreactie van +2.5 kN. Omdat we weten dat deze kracht op dit punt optreedt, we zullen alleen dit punt afzonderlijk bekijken. We herhalen dit proces een aantal keren, het is dus belangrijk om het proces te oefenen en te leren om een goed begrip te hebben van het oplossen van axiale krachten in truss-constructies. Dus weer, overweeg het eerste punt bij de ondersteuning:
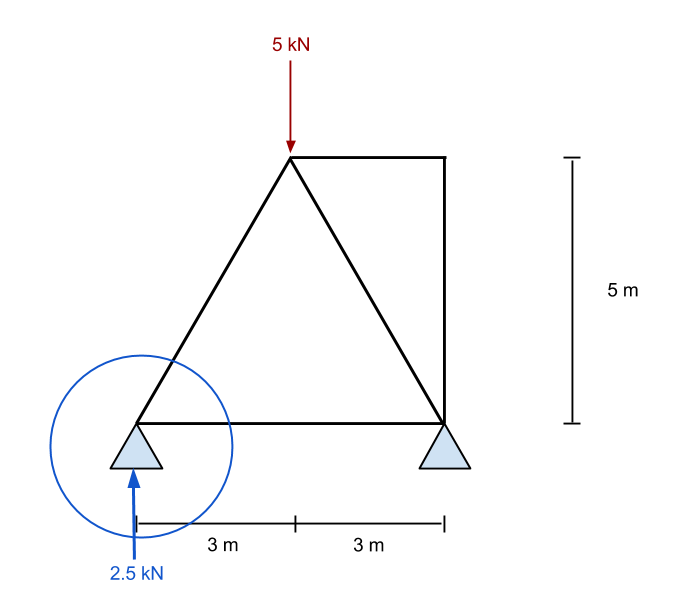
Inzoomen op dit punt, we zien alle bekende krachten op dit punt inwerken. Van statica, we weten dat de krachten in de x- en y-richting beide moeten optellen tot nul. Overeenkomstig, als we weten dat er een opwaartse verticale kracht is, dan moet er een neerwaartse kracht zijn om het tegen te gaan. Omdat we al de waarde hebben van een opwaarts gerichte kracht, dan zullen we proberen het lidnummer te evalueren 1 eerste.
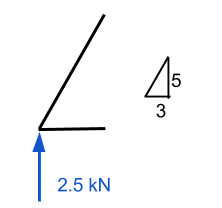
Hier hebben we enige kennis van vectoren nodig. Het is belangrijk om te onthouden dat alle krachten voor zowel de x- als de y-richting moeten optellen. In ons voorbeeld, de horizontale afstand is 3 meter, terwijl de verticale afstand 5 meter is – waardoor we de hypotenusa hebben die ongeveer gelijk is aan 5.83 m. Dit gebruiken, we kunnen afleiden dat de normale krachtcomponent van lid 1 is gelijk aan (5.83)/(5) maal de verticale kracht van 2.5 kN. Dit komt overeen met 2.92 kN en MOETEN een neerwaarts werkende kracht zijn als het punt is om stationair te blijven.
Lid 2 kan op vrijwel dezelfde manier worden berekend. Als we dat lid kennen 1 werkt naar beneden, dan weten we dat het ook naar links moet handelen. Overeenkomstig, we kennen lid 2 moet een kracht genereren die de punt naar rechts trekt om de krachten in de x-richting te houden. Deze waarde wordt berekend door (3/5.83) X 2.92 kN en is gelijk aan 1.51 kN.
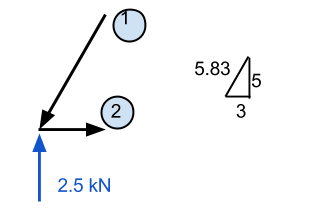
Stap 3: Ga naar een ander punt:
Nadat we de interne krachten van het eerste lid in onze truss hebben berekend, we zullen nu naar een ander punt kijken om het proces te herhalen:
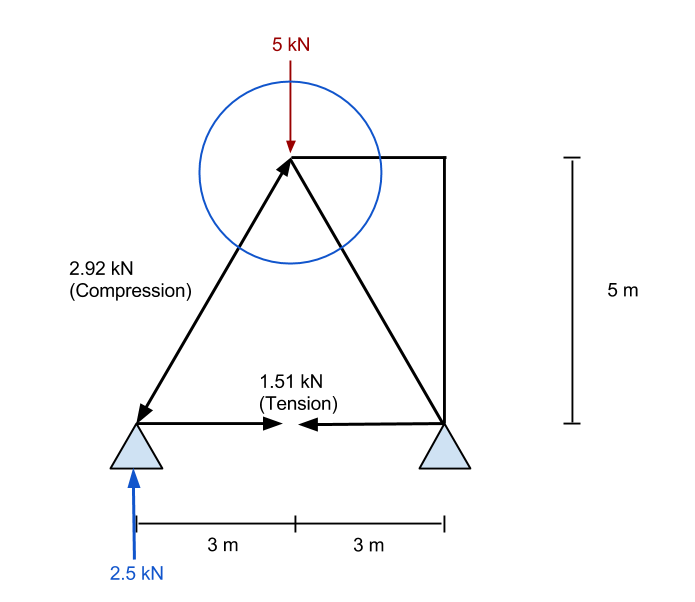
Opnieuw, we zullen inzoomen op het referentiepunt en alle bekende krachten beschouwen die op het punt inwerken:
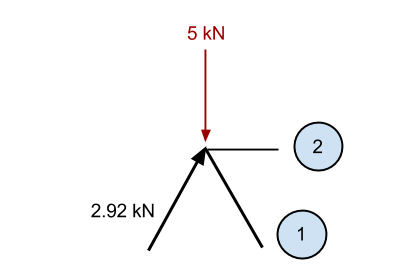
Op dezelfde manier als voorheen, als we de bekende verticale component van de 2.92 kN-lid (2.5 kN in verticale richting) als de – 5kN neerwaartse kracht, dan hebben we overmaat in de neerwaartse richting van 2.5 kN (5 – 2.5). Overeenkomstig, we kennen dat lid 1 moet een kracht in de opwaartse richting veroorzaken om het punt statisch te houden. Deze kracht moet een verticale component hebben van 2.5 kN, en omdat het in dezelfde hoek staat als het vorige lid, dan moet de interne axiale kracht ook zijn 2.92 kN.
Nu kijken we naar de krachten in de x-richting. Op dit punt, alle verticale kracht van lid 1 is weerstand bieden aan de verticale kracht van de eerder berekende staaf. Dit betekent dat de som van de krachten in de x-richting al nul is. Overeenkomstig, er kan geen kracht in Member zijn 2 anders raakt het punt uit balans en niet langer statisch.
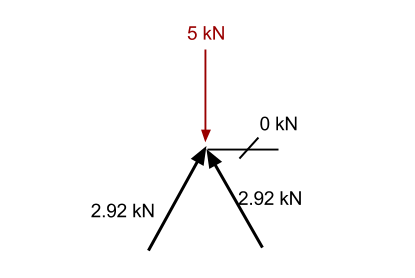
Stap 4: Ga naar een ander punt:
Kijkend naar dit punt, we kunnen zien dat er een speciaal geval is. In deze situatie, elke opduwende kracht zal geen enkele mogelijke weerstand bieden, omdat er geen ander lid is dat een neerwaartse kracht kan leveren om het punt statisch te houden. Overeenkomstig, aangezien de som van de krachten nul moet zijn, dat lid kan er geen kracht bij hebben. Het, daarom, heeft geen kracht in zich en staat bekend als een Zero-lid.
Opnieuw, als we kijken naar het optellen van de krachten in de x-richting, we kunnen zien dat er maar één lid is dat enige kracht heeft in de x-richting. Overeenkomstig, dit moet ook hebben 0 axiale kracht zodat de som van de krachten gelijk is aan nul.
Uiteindelijke oplossing
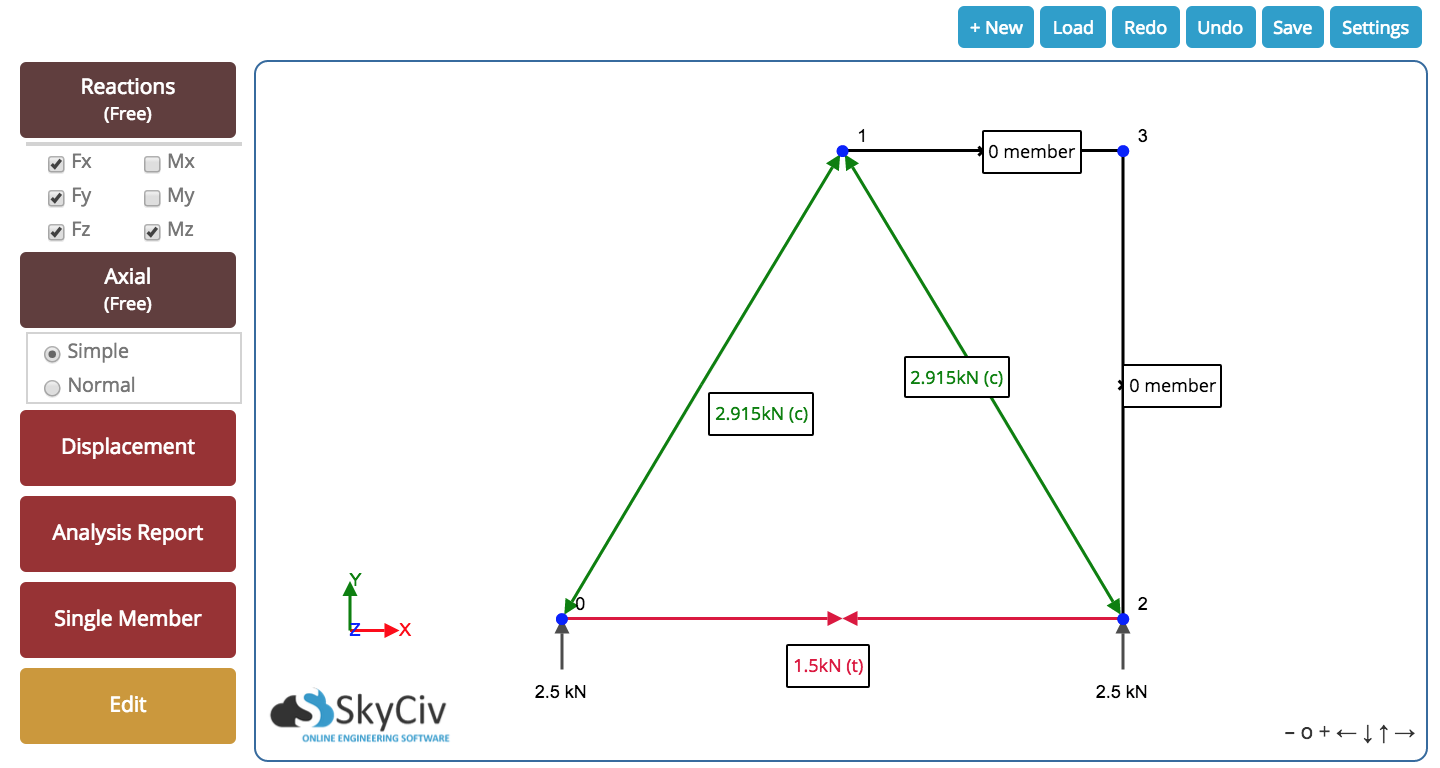
Uiteindelijk, we krijgen het volgende resultaat voor onze tros. We kunnen alle resulterende axiale krachten zien in het element en de reacties bij de steunen. Het volgende resultaat is overgenomen van onze Gratis Truss Calculator – geef het een kans, het is gratis!
Simpele stappen
- Begin altijd met het berekenen van reacties op ondersteuningen
- Kies een punt met een bekende kracht en bekijk het afzonderlijk
- Gebruik vectorgeometrie en de som van krachten = 0 om de andere ledenkrachten op te lossen
- Herhaal het proces totdat alle leden zijn opgelost
- Denk eraan om op Zero-leden te letten
Relevante zelfstudie
- Truss oplossen door middel van secties. Inclusief een video en een stapsgewijze handleiding
SkyCiv Truss
SkyCiv Truss kan de methode van verbindingen automatisch voor u berekenen. Of probeer onze Gratis Truss Calculator die je het definitieve antwoord zal geven (geen handberekeningen).
Om meer functionaliteit van SkyCiv-software te verkennen, meld je vandaag nog aan om te beginnen!
