Fundamentals of Moment of Inertia

Het traagheidsmoment kan worden afgeleid als het krijgen van de traagheidsmoment van de onderdelen en het toepassen van de overdrachtsformule: Ik = ik₀ + Advertentie². We hebben een uitgebreid artikel waarin de aanpak van het traagheidsmoment oplossen.

Fundamenteel, het traagheidsmoment is het tweede moment van gebied, wat kan worden uitgedrukt als het volgende:

[wiskunde] IK_{X}= int int y ^{2}geeft [wiskunde] [wiskunde] IK_{j}= int int x ^{2}geeft [wiskunde]

Om de afleiding van de onderstaande formules te observeren, we proberen het traagheidsmoment van een object, zoals een rechthoek om zijn hoofdas, te vinden door alleen de bovenstaande formule te gebruiken. Om het traagheidsmoment te krijgen, de grenzen moeten zo worden bepaald dat ze van de rotatieas tot aan de uiterste vezel worden overgebracht. Dit zouden de grenzen zijn van de buitenste integraal. De binnenste integraal heeft een limiet van 0 naar b. Dat gezegd hebbende, we kunnen dA ook uitdrukken als xdy, dat wordt bdy. Omdat de rotatieas zich op de neutrale as bevindt, het traagheidsmoment kan worden geïntegreerd met een bovengrens van h / 2 en een ondergrens van 0 en tweemaal vermenigvuldigd vanwege de symmetrie van de rechthoek. Dit laat ons achter met de onderstaande integraal.

[wiskunde] IK_{X}= 2 int_{0}^{\frac{h}{2}} en ^{2}bdy [wiskunde] Integreren, [wiskunde] IK_{X}= 2b links [ \frac{en ^{3}}{3} \Rechtsaf ]_{0}^{\frac{h}{2}} [wiskunde] [wiskunde] IK_{X}= 2b links [ \frac{h ^{3}}{24}-0 \Rechtsaf ] [wiskunde] [wiskunde] IK_{X}= frac{bh ^{3}}{12} [wiskunde]

Traagheidsmomentformule voor balksecties

SkyCiv heeft een samenvatting samengesteld van traagheidsmomentvergelijkingen voor balksecties (tweede moment van gebied). Traagheidsmomentvergelijkingen zijn uitermate handig voor snelle en nauwkeurige berekeningen. De formules zijn voor uw gemak samengevat in hun eenvoudigste vormen.

SkyCiv biedt ook een Gratis Traagheidsmoment Calculator voor snelle berekeningen of om te controleren of u de formule correct heeft toegepast. De traagheidsmomentformule voor rechthoek, cirkel, holle en driehoekige balksecties zijn gegeven. Enkele belangrijke dingen om te onthouden met betrekking tot het traagheidsmoment van een straal zijn::

• Oppervlaktetraagheidsmoment verschilt van het massatraagheidsmoment
• Het staat ook bekend als het tweede moment van gebied
• Het is een belangrijke factor van afbuiging (hoe groter de ik_X, de lagere doorbuiging zal zijn)
• De units hebben een lengte tot de macht van 4
• De onderstaande vergelijkingen geven het traagheidsmoment ten opzichte van het zwaartepunt van de sectie

REFERENTIE	Ixx	Ijj
Traagheidsmomentvergelijking voor rechthoekige of rechthoekige secties
	[wiskunde] \dfrac{bh ^ 3}{12} [wiskunde]	[wiskunde] \dfrac{b ^{3}h}{12} [wiskunde]
Traagheidsmomentvergelijking voor een holle rechthoekige doorsnede
	[wiskunde] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [wiskunde]	[wiskunde] \dfrac{b ^ 3h}{12} – \dfrac{b_1 ^ 3h_1}{12} [wiskunde]
Traagheidsmomentvergelijking voor een cirkel of cirkelvormige doorsnede
	[wiskunde] \dfrac{\pi}{64}D ^ 4 [wiskunde]	[wiskunde] \dfrac{\pi}{64}D ^ 4 [wiskunde]
Traagheidsmomentvergelijking voor een holle cirkelvormige doorsnede
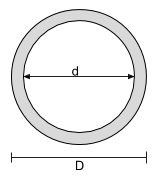	[wiskunde] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [wiskunde]	[wiskunde] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [wiskunde]
Traagheidsmomentvergelijking voor een gelijkbenige driehoek
	[wiskunde] \dfrac{bh ^ 3}{36} [wiskunde]	[wiskunde] \dfrac{3b ^ 3h}{144} [wiskunde]
Traagheidsmomentvergelijking van een I-sectie
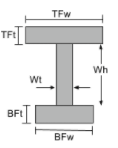	[wiskunde] \frac{TFw tijden TFt ^{3}}{12} +\frac{Wt maal Wh ^{3}}{12} + \frac{BFw maal BFt ^{3}}{12} +[wiskunde] [wiskunde] TFw times TFt times left ( BFt + Wh + frac{TFt}{2} -\bar{j}_{bot} \Rechtsaf )^{2} +[wiskunde] [wiskunde] Wt maal Wh maal links ( BFt + frac{Wh}{2} -\bar{j}_{bot} \Rechtsaf )^{2} +[wiskunde] [wiskunde] BFw keer BFt keer links ( \frac{Wh}{2} -\bar{j}_{bot} \Rechtsaf )^{2} [wiskunde]	[wiskunde] \frac{TFt maal TFw ^{3}}{12} + \frac{Wh times Wt ^{3}}{12} + \frac{BFt maal BFw ^{3}}{12} [wiskunde]
Traagheidsmomentvergelijking van een T-sectie
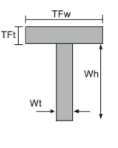	[wiskunde] \frac{TFw tijden TFt ^{3}}{12} + \frac{Wt maal Wh ^{3}}{12} +[wiskunde] [wiskunde] TFw times TFt left ( Wh + \frac{TFt}{2} -\bar{j}_{bot} \Rechtsaf )^{2} +[wiskunde] [wiskunde] Wt maal Wh maal links ( \frac{Wh}{2} – \bar{j}_{bot} \Rechtsaf )^{2} [wiskunde]	[wiskunde] \frac{TFt maal TFw ^{3}}{12} + \frac{Wh times Wt ^{3}}{12} [wiskunde]
Traagheidsmomentvergelijking van een kanaalsectie
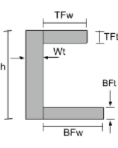	[wiskunde] \frac{TFw tijden TFt ^{3}}{12} + \frac{BFw maal BFt ^{3}}{12} + \frac{Wt maal h ^{3}}{12} +[wiskunde] [wiskunde] TFw times TFt times left ( h – \frac{TFt}{2} – \bar{j}_{bot} \Rechtsaf )^{2} +[wiskunde] [wiskunde] BFw times BFt times left ( \frac{BFt}{2} – \bar{j}_{bot} \Rechtsaf )^{2} +[wiskunde] [wiskunde] Wt times h times left ( \frac{h}{2} – \bar{j}_{bot} \Rechtsaf )^{2} [wiskunde]	[wiskunde] \frac{TFt maal TFw ^{3}}{12} + \frac{BFt maal BFw ^{3}}{12} + \frac{h tijden Wt ^{3}}{12} +[wiskunde] [wiskunde] TFt times TFw times left ( Wt + \frac{TFw}{2} – \bar{X}_{links} \Rechtsaf )^{2} +[wiskunde] [wiskunde] BFt keer BFw keer links ( Wt + \frac{BFw}{2} – \bar{X}_{links} \Rechtsaf )^{2} +[wiskunde] [wiskunde] h times Wt times left ( \frac{Wt}{2} – \bar{X}_{links} \Rechtsaf )^{2} [wiskunde]
Moment of Inertia Vergelijking van hoeken
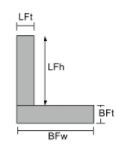	[wiskunde] \frac{BFw maal BFt ^{3}}{12} + \frac{ LFt maal LFh ^{3}}{12} +[wiskunde] [wiskunde] BFw keer BFt keer links ( \frac{BFt}{2}-\bar{j}_{bot} \Rechtsaf )^{2} +[wiskunde] [wiskunde] LFt keer LFh keer links ( BFt + \frac{LFh}{2}-\bar{j}_{bot} \Rechtsaf )^{2} [wiskunde]	[wiskunde] \frac{BFt maal BFw ^{3}}{12} + \frac{ LFh maal LFt ^{3}}{12} +[wiskunde] [wiskunde] BFt keer BFw keer links ( \frac{BFw}{2}-\bar{X}_{links} \Rechtsaf )^{2} +[wiskunde] [wiskunde] LFh keer LFt keer links ( \frac{Als T}{2}-\bar{X}_{links} \Rechtsaf )^{2} [wiskunde]

Gebruik SkyCiv Section Builder voor handberekeningen

In dit artikel, we hebben je door de formule van het traagheidsmoment geleid. Voor meer informatie over dit onderwerp, bezoek onze tutorial op Traagheidsmoment van straalsectie.

Wist u SkyCiv Sectiebouwer toont ook de volledige handberekeningen voor de volgende vormen?

• Rechthoekig, Hol rechthoekig
• Circulaire, Hol rond
• I-Beam, T-balk
• Hoek (L-Beam), Kanaal
• Driehoekige secties

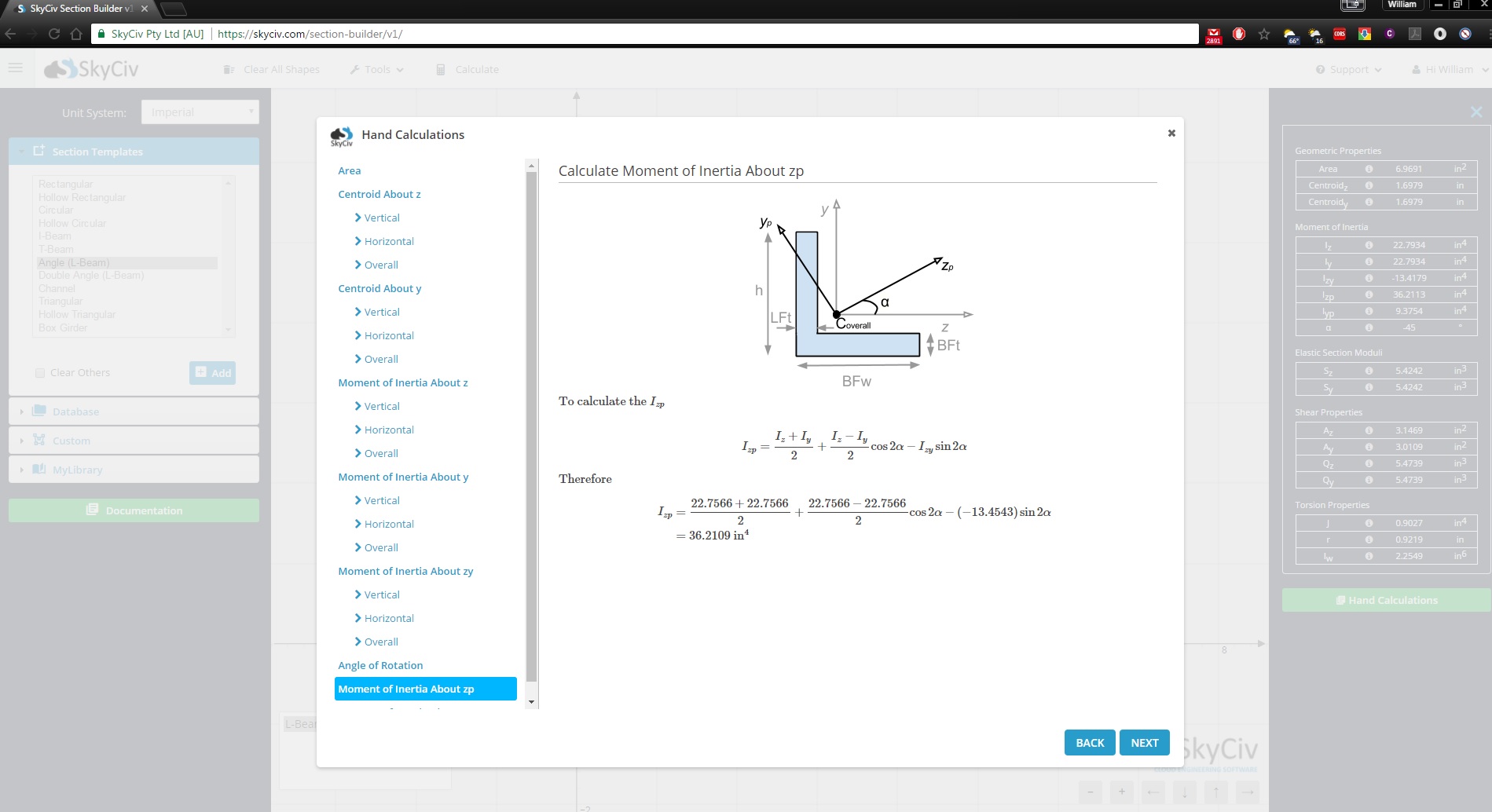
We hopen dat u de bovenstaande tabel waardevol vindt voor het berekenen van een traagheidsmoment van een cirkel, driehoek, en rechthoekig traagheidsmoment onder andere vormen. We hebben ook een handige Moment of Inertia Calculator, een vereenvoudigde van SkyCiv Sectiebouwer, die deze berekeningen voor u afhandelt of meld u vandaag nog aan om aan de slag te gaan met SkyCiv-software!