Hoe een onbepaalde straal te berekenen – Dubbele integrale methode

onbepaald balken kan een uitdaging zijn vanwege de extra stappen die nodig zijn om de reacties op te lossen. Bedenk dat onbepaalde structuren een zekere mate van onbepaaldheid hebben. Om de structuur op te lossen, randvoorwaarden moeten worden ingevoerd. bijgevolg, hoe hoger de mate van onbepaaldheid, de meer randvoorwaarden moeten worden geïdentificeerd. Maar voordat we een onbepaalde balk kunnen oplossen, we moeten eerst bepalen of de straal statisch onbepaald is. Omdat balken eendimensionale structuren zijn, het gebruik van de vergelijking om extern statisch onbepaalde structuren te bepalen is voldoende.

[wiskunde]
ik_{e}= R- links ( 3+e_{c} \Rechtsaf )
[wiskunde]

Waarbij:

• ik_e = Mate van onbepaaldheid
• R = Totaal aantal reacties
• e_c = Externe voorwaarden (bijv. intern scharnier)

Typisch, echter, zonder de noodzaak op te lossen voor de mate van onbepaaldheid, iets anders dan eenvoudige overspanningen of vrijdragende liggers zijn statisch onbepaald, ervan uitgaande dat dergelijke balken niet met interne scharnieren worden geleverd.

Er zijn veel manieren om het te benaderen, het gaat om het oplossen van onbepaalde balken. Hoewel omwille van de eenvoud en gelijkenis met SkyCiv Beam's handmatige berekeningen, we zullen de methode van dubbele integratie bespreken.

Dubbele integratie

Dubbele integratie is misschien wel de eenvoudigste van alle methoden voor de analyse van balken. Het concept voor deze methode is vrij eenvoudig in tegenstelling tot andere methoden, omdat het voornamelijk afhankelijk is van een basiskennis van integraalrekening, Vandaar de naam. Een beetje integraalrekening is aangepast van de relatie van de kromming van de balk tot het moment dat hieronder wordt weergegeven.

[wiskunde]
\frac{1}{\rho}= frac{M}{NEE}
[wiskunde]

Merk op dat 1 / ρ de kromming van de staaf is en dat ρ de straal van de kromme is. Fundamenteel, de definitie van kromming is de snelheid waarmee de tangens verandert ten opzichte van de booglengte. Omdat het moment een functie is van de belasting ten opzichte van de lengte van het lid, het integreren van de kromming met betrekking tot de lengte van het lid zal de helling van de balk opleveren. Evenzo, het integreren van de helling ten opzichte van de lengte van het element zal de straalafbuiging opleveren. Typische structurele belastingen zijn algebraïsch van aard, integratie van deze uitdrukkingen is net zo eenvoudig als het gebruik van de algemene machtsformule.

[wiskunde]
\int f left ( x juist )^{n}dx = frac{f links ( x juist )^{n + 1}}{n + 1}+C
[wiskunde]

Misschien is de beste manier om het concept te begrijpen, door een voorbeeld van een balk te geven met het volgende gegeven.

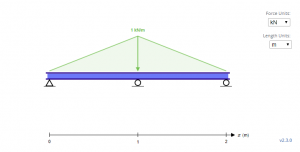
De voorbeeldstraal hierboven is een onbepaalde ligger met driehoekige belastingen. Met de ondersteuning, A_j, B_j en C_j voor het eerst, tweede, en derde steunen respectievelijk, de eerste stap bij het oplossen van deze onbekenden is door te beginnen met de evenwichtsvergelijkingen.

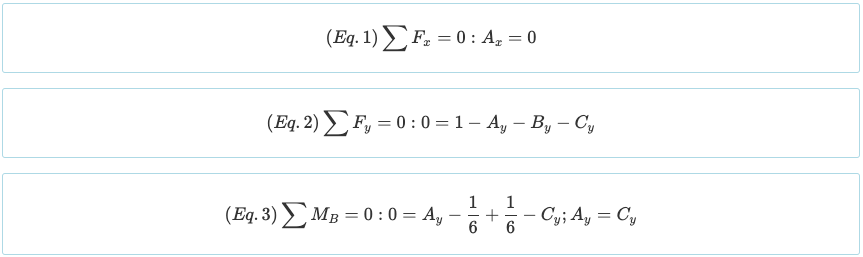
Merk op dat de straal een graad van heeft statische onbepaaldheid van 1°. Omdat er vier onbekenden zijn (A_X, A_j, B_j, en C_j) en er zijn tot dusver drie vergelijkingen van de bovenstaande evenwichtsvergelijkingen, het is noodzakelijk om nog een vergelijking te maken op basis van de randvoorwaarden. Bedenk dat het moment dat wordt gegenereerd door een puntbelasting en een driehoekige belasting de volgende zijn.

Puntbelasting:

[wiskunde]
M = F maal x; M = Fx
[wiskunde]

Driehoekige lading:

[wiskunde]
M = frac{w_{0}\keer x}{2}\keer links ( \frac{X}{3} \Rechtsaf ); M = frac{w_{0}x ^{2}}{6}
[wiskunde]

Door dubbele integratiemethode te gebruiken, deze nieuwe vergelijkingen worden gemaakt en hieronder weergegeven.

Notitie: De bovenstaande vergelijkingen zijn geschreven als Macaulay-functies waarbij een uitdrukking gelijk is aan nul wanneer X < L. In dit geval, L = 1.

In de bovenstaande vergelijkingen, merk op dat de vierde toegevoegde term uit het niets lijkt te komen. In feite, de richting van de lading is tegengesteld aan de richting van de zwaartekracht. Dit komt door het feit dat de vergelijkingen voor driehoekige belastingen alleen werken als de belasting stijgt naarmate de lengte toeneemt. Dit is niet echt een probleem voor vergelijkingen voor gedistribueerd en puntbelastingen vanwege hun symmetrie. In werkelijkheid, de equivalente belasting voor de balk hierboven ziet eruit als de balk eronder, dus de vergelijkingen zijn erop gebaseerd.

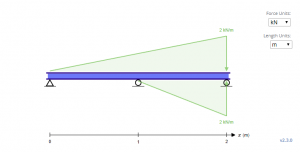
Om C op te lossen₁ en C₂, de randvoorwaarden moeten worden bepaald. In de balk hierboven, het kan worden opgemerkt dat er drie van dergelijke randvoorwaarden bestaan ​​bij X = 0, X = 1, en X = 2, waarbij de doorbuiging y nul is op de drie locaties.

Randvoorwaarde 1

[wiskunde]
x = 0, y = 0; C_{2}= 0
[wiskunde]

Randvoorwaarde 2

[wiskunde]
x = 0, y = 0; C_{1}= frac{1}{120}-\frac{EEN_{j}}{6}
[wiskunde]

Na het bepalen van de waarden van elke constante, de laatste vergelijking kan nu worden verkregen met behulp van de laatste randvoorwaarde.

Randvoorwaarde 3

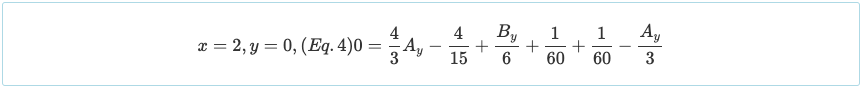
Merk op dat de randvoorwaarde van θ = 0 bij x = 1 kan worden gebruikt, hoewel het alleen van toepassing is voor de middelste reactie van een symmetrische continue straal met symmetrische belasting.

Omdat de vier vergelijkingen zijn bepaald, ze kunnen nu gelijktijdig worden opgelost. Het oplossen van deze vergelijkingen zal de volgende reacties opleveren.

Met de reacties bepaald, de waarden van de reacties kunnen terug naar de momentvergelijking worden vervangen. Dit stelt ons in staat om de waarde van het moment in elk deel van het straalsysteem te bepalen.

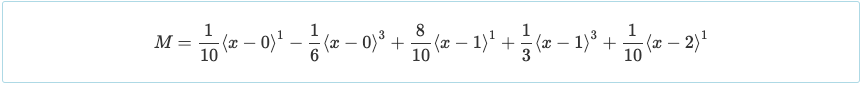
Een ander gemak van dubbele integratie is dat de momentvergelijking wordt gepresenteerd op een manier die kan worden gebruikt om afschuiving op te lossen met de onderstaande relatie.

[wiskunde]
V = frac{dM}{dx}
[wiskunde]

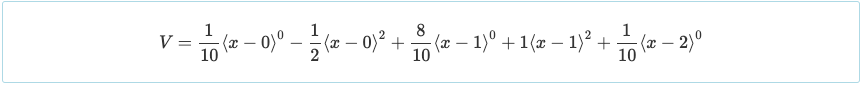
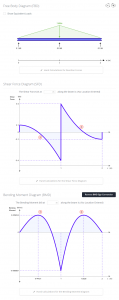
Opnieuw, alleen een basiskennis van differentiaalrekening gebruiken, het gelijkstellen van de afgeleide van een functie aan nul geeft het maximum of minimum van die functie. Dus, gelijk aan V = 0 zal resulteren in een maximaal positief moment op X = 0.447 en X = 1.553 van M = 0.030

Natuurlijk, dit alles kan worden geverifieerd met SkyCiv Beam.

SkyCiv Balk Software

SkyCiv Balk Analyse Software stelt gebruikers in staat om balkconstructies eenvoudig en nauwkeurig te analyseren. Je kunt binnen enkele seconden een analyse van je balkelement krijgen, inclusief reacties, dwarskracht, buigmoment, doorbuiging, en benadrukt in een kwestie van seconden.

Als je het eerst wilt proberen, Gratis Balk Calculator een geweldige manier om te beginnen, of meld je vandaag nog gratis aan!