De grondbeginselen van het zwaartepunt
Het is belangrijk op te merken dat op een doorsnede, wiens gebied overal uniform is, het zwaartepunt kan worden gevonden door de som van momenten te nemen ten opzichte van een willekeurig ingestelde as, maar wordt meestal op de bovenste of onderste vezel geplaatst. Bekijk ons vorige artikel op hoe het zwaartepunt te vinden van een straalsectie en SkyCiv Free Centroid Calculator.
Fundamenteel, het zwaartepunt kan worden verkregen door de som van momenten te nemen over de som van het gebied. Dat wordt op deze manier uitgedrukt.
[wiskunde]
\bar{X}= frac{1}{A}\int xf left ( x juist )dx
[wiskunde]
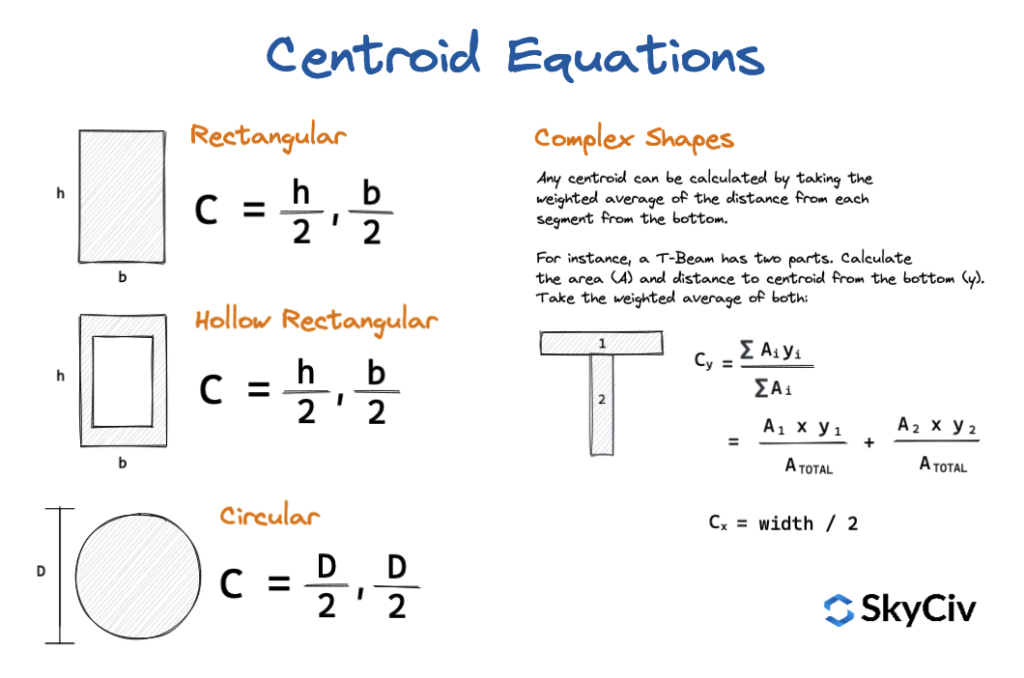
Samenvatting van zwaartepuntvergelijkingen
In de bovenstaande vergelijking, f(X) is de functie en x is de momentarm. Om dit beter te illustreren, we zullen het y-zwaartepunt afleiden van een willekeurige driehoek waarvan de basis samenvalt met de x-as. In deze situatie, de vorm van de driehoek, of het nu gelijkzijdig is, isosceles of scalene is niet relevant aangezien alles relatief is ten opzichte van alleen de x-as. Merk op dat de vorm niet relevant is als de basis van de driehoek samenvalt of parallel is met de as. Dit zal niet het geval zijn bij het oplossen van het x centroïde. In plaats daarvan, je kunt je voorstellen dat het het zwaartepunt van twee rechthoekige driehoeken krijgt ten opzichte van de y-as. Gemakshalve, laten we ons een gelijkbenige driehoek voorstellen die lijkt op de onderstaande referentietabel. Het vinden van de relatie tussen b en h levert de volgende relatie op:.
[wiskunde]
\frac{-j}{X}= frac{-h}{b}
[wiskunde]
Merk op dat de helling negatief is, aangezien we ons voorstellen dat de driehoek rechtop staat. Als we ons voorstellen dat de driehoek wordt omgekeerd, de helling zou positief zijn. Hoe dan ook, de relatie blijft hetzelfde. Zoals x = f(j), de bovenstaande relatie kan als volgt worden herschreven.
[wiskunde]
x = f links ( y juist )= frac{b}{h}j
[wiskunde]
We kunnen nu het zwaartepunt oplossen. De eerste vergelijking hierboven aanpassen, we krijgen het volgende.
[wiskunde]
\bar{j}= frac{1}{A}\int yf left ( y juist )twee
[wiskunde]
Door aanvullende waarden in te pluggen en de bovenstaande relatie te vervangen, wordt de volgende vergelijking verkregen.
[wiskunde]
\bar{j}= frac{2}{bh}\int_{0}^{h} \frac{b}{h}en ^{2}twee
[wiskunde]
Vereenvoudigen,
[wiskunde]
\bar{j}= frac{2}{h ^{2}}\links [ \frac{en ^{3}}{3} \Rechtsaf ]_{0}^{h}
[wiskunde]
[wiskunde]
\bar{j}= frac{2}{h ^{2}}\links [ \frac{h ^{3}}{3}-0 \Rechtsaf ]
[wiskunde]
[wiskunde]
\bar{j}= frac{2}{3}h
[wiskunde]
Merk op dat deze oplossing van bovenaf wordt genomen. Het zwaartepunt genomen vanaf de onderkant moet dan gelijk zijn aan 1/3 van h.
Formule voor zwaartepunten met veel voorkomende vormen en liggerdoorsneden
Hieronder is een lijst van a verscheidenheid aan balkprofielvormen en de afstand tot de zwaartepunten van de sectie. De vergelijkingen laten zien hoe je het zwaartepunt van een bepaalde sectie kunt vinden vanaf de basis of het meest linkse punt van de sectie. Voor SkyCiv Student- en structurele abonnementen, deze referentie kan ook worden gedownload als PDF-referentie om overal mee naartoe te nemen. Centralen van een balksectie zijn uiterst belangrijk omdat ze de neutrale as lokaliseren en een van de eerste stappen zijn die nodig zijn bij het analyseren van een balksectie.
SkyCiv biedt ook een uitgebreide samenvatting van sectiestabel die alle vergelijkingen en formules bevat met betrekking tot balksecties (traagheidsmoment, gebied enz…).
De vergelijking voor verschillende centroïden wordt hieronder vermeld:
| REFERENTIE | Cj (Afstand vanaf de onderkant) |
CX (Afstand vanaf het verste linkerpunt) |
Zwaartepunt van rechthoekige of rechthoekige secties |
||
|---|---|---|
 |
[wiskunde] \dfrac{h}{2} [wiskunde] |
[wiskunde] \dfrac{b}{2} [wiskunde] |
Zwaartepunt van een holle rechthoekige doorsnede |
||
 |
[wiskunde] \dfrac{b}{2} [wiskunde] |
[wiskunde] \dfrac{h}{2} [wiskunde] |
Zwaartepunt van een cirkel of cirkelvormig gedeelte |
||
 |
[wiskunde] \dfrac{D}{2} [wiskunde] |
[wiskunde] \dfrac{D}{2} [wiskunde] |
Centroid-vergelijking van een holle cirkelvormige doorsnede |
||
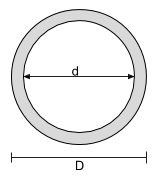 |
[wiskunde] \dfrac{D}{2} [wiskunde] |
[wiskunde] \dfrac{D}{2} [wiskunde] |
Zwaartepunt van een gelijkbenige driehoek |
||
 |
[wiskunde] \dfrac{h}{3} [wiskunde] |
[wiskunde] \dfrac{b}{2} [wiskunde] |
Zwaartepunt van een I Beam |
||
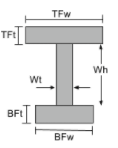 |
[wiskunde] \frac{TFw times TFt times left ( BFt + Wh + \frac{TFt}{2} \Rechtsaf )}{TFw maal TFt + Wt maal Wh + BFw maal BFt} + [wiskunde] [wiskunde] \frac{Wt maal Wh maal links ( BFt + \frac{Wh}{2} \Rechtsaf )}{TFw maal TFt + Wt maal Wh + BFw maal BFt} + [wiskunde] [wiskunde] \frac{BFw keer BFt keer links ( \frac{BFt}{2} \Rechtsaf )}{TFw maal TFt + Wt maal Wh + BFw maal BFt} [wiskunde] |
[wiskunde] TFw > BFw, \frac{TFw}{2}[wiskunde] [wiskunde] BFw > TFw, \frac{BFw}{2} [wiskunde] |
Zwaartepunt van een T-sectie |
||
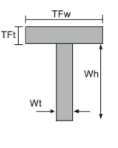 |
[wiskunde] \frac{Wt maal Wh maal links ( \frac{Wh}{2} \Rechtsaf )}{TFw maal TFt + Wt maal Wh } + [wiskunde] [wiskunde] \frac{TFw times TFt times left ( Wh + \frac{TFt}{2} \Rechtsaf ) }{TFw maal TFt + Wt maal Wh } [wiskunde] |
[wiskunde] \frac{TFw}{2} [wiskunde] |
Zwaartepunt van een C-sectie |
||
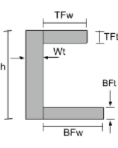 |
[wiskunde] \frac{TFw times TFt times left ( h – \frac{TFt}{2} \Rechtsaf )}{TFw maal TFt + Wt maal Wh + BFw maal BFt} + [wiskunde] [wiskunde] \frac{Wt times h times left ( \frac{h}{2} \Rechtsaf )}{TFw maal TFt + Wt maal Wh + BFw maal BFt} + [wiskunde] [wiskunde] \frac{BFw keer BFt keer links ( \frac{BFt}{2} \Rechtsaf )}{TFw maal TFt + Wt maal Wh + BFw maal BFt} [wiskunde] |
[wiskunde] \frac{TFt times TFw times left ( Wt + \frac{TFw}{2} \Rechtsaf )}{TFt keer TFw + h maal gew + BFt maal BFw} + [wiskunde] [wiskunde] \frac{h times Wt times left ( \frac{Wt}{2} \Rechtsaf )}{TFt keer TFw + h maal gew + BFt maal BFw} + [wiskunde] [wiskunde] \frac{BFt keer BFw keer links ( Wt + \frac{BFw}{2} \Rechtsaf )}{TFt keer TFw + h maal gew + BFt maal BFw} [wiskunde] |
Zwaartepunt van een hoeken |
||
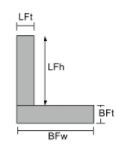 |
[wiskunde] \frac{LFt keer LFh keer links ( BFt + \frac{LFh}{2} \Rechtsaf ) }{LFt maal LFh + BFw maal BFt} + [wiskunde] [wiskunde] \frac{BFw keer BFt keer links ( \frac{BFt}{2} \Rechtsaf )}{LFt maal LFh + BFw maal BFt} [wiskunde] |
[wiskunde] \frac{LFh keer LFt keer links ( \frac{Als T}{2} \Rechtsaf )}{LFh maal LFt + BFt maal BFw} + [wiskunde] [wiskunde] \frac{BFt keer BFw keer links ( \frac{BFw}{2} \Rechtsaf )}{LFh maal LFt + BFt maal BFw} [wiskunde] |
Automatische vergelijkingen voor zwaartepunt van straal
Bekijk onze Gratis centroid rekenmachine, een vereenvoudigde versie van SkyCiv Sectiebouwer, om het zwaartepunt van de straal automatisch te berekenen zonder dat handmatige berekeningen nodig zijn. Of meld je vandaag nog aan om te beginnen!


