Laterale aarddruk op een keermuur berekenen

Een van de belangrijkste belastingen die op een keermuur werken, is de zijdelingse gronddruk. Om die reden, een goede inschatting maken van de omvang en verdeling is bepalend bij het ontwerp van een betonnen keermuur. Over het algemeen, er zijn drie verschillende soorten zijdelingse gronddruk, afhankelijk van de richting waarin de muur neigt te bewegen:

• Gronddruk in rust: Wanneer de muur volledig verhinderd is om te bewegen
• Actieve gronddruk: Wanneer de muur weg kan kantelen van de vastgehouden grond
• Passieve gronddruk: Wanneer de muur in de vastgehouden grond mag worden geduwd

In dit artikel, we zullen ons concentreren op het beschrijven van de formules voor elk van de bovengenoemde gevallen van gronddruk.

Laterale verdeling van de gronddruk

Over het algemeen, laterale gronddruk gedraagt ​​zich hetzelfde als hydrostatische druk. Een nulwaarde hebben aan de oppervlakte en een maximale waarde op het diepste punt na een lineaire verdeling tussen de twee genoemde grenzen. Daarom, de horizontale spanningsverdeling onder het oppervlak wordt beschreven door de volgende uitdrukking::

\(\sigma_h = K_* cdot (\gamma z)\)

Waarbij \(K_*) neemt de waarde van \(K_o\) voor het geval van rustdruk, \(K_a\) voor het geval van actieve druk, en \(K_p\) voor het geval van passieve druk.

Integratie van de gegeven uitdrukking voor de laterale ondergrondspanning van \(0\) naar \(H\) in \(z), het resultaat blijkt te zijn:

\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)

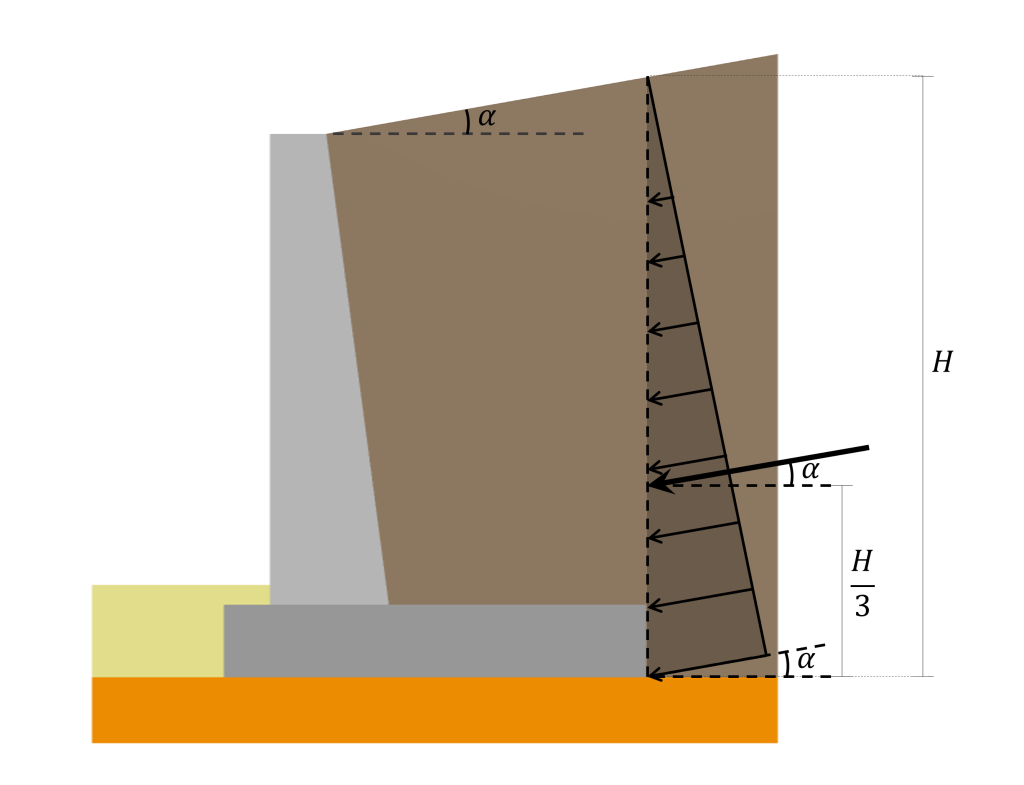
De actielijn van deze resultante bevindt zich \(\frac{2}{3}H\) vanaf de oppervlakte. De laterale gronddrukverdeling, zijn resultante, en locatie hierboven beschreven worden geïllustreerd in de volgende afbeelding::

Het is belangrijk om te vermelden dat de gepresenteerde distributie en resulterende berekeningsbenadering alleen van toepassing is op bodemdrukken die inwerken op een verticaal achtervlak. In het geval van een keermuur met een schuine achterkant (zoals die op de foto hierboven), het oppervlak waar de bodemdruk werkt, wordt nog steeds als verticaal beschouwd, aangezien wordt aangenomen dat het werkt in een verticaal vlak op de plaats waar de hiel eindigt.

Bovendien, wanneer de opvulling onder een bepaalde hoek helt \(\alfa) met betrekking tot de horizontale, de drukverdeling en de resultante ervan hellen onder dezelfde hoek \(\alfa) zoals geïllustreerd in het volgende::

Het correct inschatten van de laterale gronddrukverdeling en het resultaat daarvan is een cruciale stap in het ontwerpproces van de keermuur. Voor meer informatie over hoe deze laterale gronddruk is opgenomen in het ontwerpproces van de keermuur, zie het artikel hier. Laten we nu ingaan op de formules voor het berekenen van de resulterende laterale gronddruk die door de grond op een keermuur wordt uitgeoefend onder verschillende omstandigheden.

Laterale gronddruk in rust

Deze benadering voor het berekenen van de zijdelingse gronddruk tegen een keermuur kan alleen worden gebruikt als de muur volledig in rust is en niet van de grond of in de grond mag bewegen, deze toestand zorgt ervoor dat de horizontale belasting in de bodem nul is. In dit geval, de coëfficiënt van rustdruk (\(K_o\)) is degene die vervangt \(K_*) in de vorige vergelijkingen. Die coëfficiënt is de enige onbekende voor het berekenen van de drukverdeling en de resulterende. Voor normaal geconsolideerde grond, de relatie voor \(K_o\) is:

\(K_o = 1-sin(\de weerstand van het eenheidspunt:)\)

Waarbij \(\[object Window]) is de effectieve wrijvingshoek van de grond in overweging.

Voor overgeconsolideerde grond, de coëfficiënt kan worden berekend met behulp van de volgende uitdrukking::

\(K_o = (1-zonder(\de weerstand van het eenheidspunt:))\cdot OCR^{zonder(\de weerstand van het eenheidspunt:)}\)

Waarbij \(\[object Window]) is de effectieve wrijvingshoek, en \(OCR\) de overconsolidatieverhouding van de grond in overweging.

Door deze coëfficiënt in te voegen in de uitdrukking voor het berekenen van de resulterende kracht uit de laterale gronddruk in rust, wordt:

\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)

Actieve laterale gronddruk

De vorige benadering kan worden gebruikt wanneer de muur helemaal niet meegeeft, echter, als een muur de neiging heeft om van de grond weg te bewegen, de bodemdruk op de muur op elke diepte zal afnemen. In dit geval, de coëfficiënt van actieve druk (\(K_a\)) is degene die vervangt \(K_*) in de eerste vergelijkingen. De aanpak van Rankine gebruiken voor een korrelige aanvulling, en ervan uitgaande dat de druk werkt in a verticale achterkant, de actieve gronddrukcoëfficiënt kan worden berekend met behulp van de vergelijking:

\(K_a=cos(\alfa) \frac{omdat(\alfa) – \sqrt{cos^2(\alfa) – cos^2(\de weerstand van het eenheidspunt:)}}{omdat(\alfa) + \sqrt{cos^2(\alfa) – cos^2(\de weerstand van het eenheidspunt:)}}\)

Waarbij \(\[object Window]) is de wrijvingshoek van de grond in overweging en \(\alfa) is de hellingshoek van het opvulvlak ten opzichte van de horizontaal.

Als u deze coëfficiënt invoegt in de uitdrukking voor het berekenen van de resulterende kracht van de laterale gronddruk bij actieve toestand, levert dit op::

\(P_a=frac{1}{2} \gamma cdot H^2 cdot K_a)

De eerder gepresenteerde berekeningen van de actieve druk van Rankine zijn gebaseerd op de aanname dat de muur wrijvingsloos is.

Passieve laterale gronddruk

De zijdelingse gronddruk die op een keermuur inwerkt, wordt als passief beschouwd wanneer de muur in de grondmassa wordt geduwd, in die toestand, de horizontale spanning zal toenemen ten opzichte van de rusttoestand. In dit geval, de coëfficiënt van passieve druk (\(K_p\)) is degene die vervangt \(K_*) in de eerste vergelijkingen. De aanpak van Rankine gebruiken voor een korrelige aanvulling, en ervan uitgaande dat de druk werkt in a verticale achterkant, de passieve gronddrukcoëfficiënt kan worden berekend met behulp van de uitdrukkingen:

Wanneer de opvulling volledig horizontaal is

\(K_p = bruin^2(45º+\frac{\de weerstand van het eenheidspunt:}{2})\)

Wanneer de opvulling een bepaalde hoek helt ten opzichte van de horizontaal

\(K_p=cos(\alfa) \frac{omdat(\alfa) + \sqrt{cos^2(\alfa) – cos^2(\de weerstand van het eenheidspunt:)}}{omdat(\alfa) – \sqrt{cos^2(\alfa) – cos^2(\de weerstand van het eenheidspunt:)}}\)

Waarbij \(\[object Window]) is de wrijvingshoek van de grond in overweging en \(\alfa) is de hellingshoek van het opvulvlak ten opzichte van de horizontaal.

Als u deze coëfficiënt invoegt in de uitdrukking voor het berekenen van de resulterende kracht van de laterale gronddruk bij passieve toestand, levert dit op::

\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)

Opnieuw, de eerder gepresenteerde berekeningen van de actieve druk van Rankine zijn gebaseerd op de aanname dat de muur wrijvingsloos is.

Referenties

Keermuurcalculator

SkyCiv biedt een gratis keermuurcalculator die de laterale gronddruk op de muur berekent, en voer een stabiliteitsanalyse uit op uw keerwanden. De betaalde versie toont ook de volledige berekeningen, zodat je stap voor stap kunt zien, hoe de stabiliteit van een keermuur tegen kantelen te berekenen?, glijden, en lager!

Keermuurcalculator