目录
总览 – 什么是惯性矩?
在结构工程背景下, 惯性矩是一种截面属性,用于确定结构元件抵抗弯曲和扭转力的能力. 它通常是负载下截面刚度和强度的一个很好的指标. 较高的转动惯量意味着结构能够更好地抵抗弯曲和偏转, 使其成为梁设计的重要因素, 列, 以及其他承重部件. 作为旁注: 有时这被错误地定义为第二时刻 详细分解, 然而这是不正确的. 转动惯量的其他名称是: 面积惯性矩, 或第二个时刻 区域.
例 – 如何计算梁截面的惯性矩
在我们找到梁截面的转动惯量之前 (也称为梁截面面积的二阶矩), 它的质心 (或质心) 必须知道. 例如, 如果截面的惯性矩关于其水平方向 (XX) 需要轴,然后垂直 (和) 首先需要质心 (请查看我们的教程 计算梁截面的质心 和 计算面积的静力/一阶矩).
开始之前, 如果您正在寻找我们的 惯性矩免费计算器 请点击链接了解更多信息. 这将计算质心, 惯性矩, 和其他结果,甚至向您展示分步计算! 但现在, 让我们看一下分步指南以及如何计算惯性矩的示例:
步 1: 将梁截面分段
计算面积惯性矩, 我们必须计算较小部分的惯性矩. 尝试将它们分成简单的矩形部分. 例如, 考虑下面的工字梁部分, 在我们的质心教程中也有介绍. 我们选择将本节分为 3 矩形段:
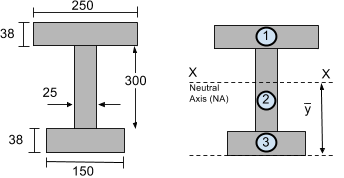
步 2: 计算中性轴 (不适用)
中性轴 (不适用) 或水平XX轴位于质心或质心. 在我们的质心教程中, 先前发现此部分的质心是 216.29 距截面底部的毫米 – 这在我们的 如何找到形状的质心 教程. 这些也可以简单地从我们的 本文将指导您完成如何计算质心的简单过程 或从普通 质心方程.
计算质心, 或中性轴, 是必不可少的 如何计算梁的转动惯量, 因为这是转动惯量作用的轴.
步 3: 计算惯性矩
要计算截面的总惯性矩,我们需要使用 “平行轴定理”:

由于我们将其分为三个矩形部分, 我们必须计算每个部分的惯性矩. 众所周知,矩形绕其质心轴的惯性矩方程很简单:
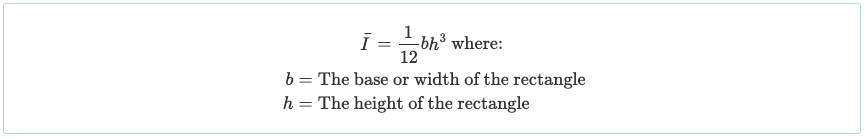
其他形状的惯性矩通常在教科书的前/后或本手册的本指南中说明。 惯性矩形状. 但是,矩形截面对于梁截面非常普遍, 所以可能值得记住.
现在我们掌握了使用 “平行轴定理” 并找到工字梁部分的总惯性矩. 以我们的惯性矩为例:

因此,您在计算梁截面的矩面积时有我们的指南. 该结果对于结构工程至关重要,并且是梁偏转的重要因素。. 希望您喜欢本教程,并希望对您有任何意见. 想要查询更多的信息, 请访问我们的教程 惯性矩公式和方程式.
公式和方程
各节类型 (长方形, 我束, 圆) 有自己的快速计算公式. 这些是简化的方程,可让工程师快速轻松地计算这一重要属性.
这些方程是上述步骤的简化表达式. 例如, 空心矩形的转动惯量公式基本上是较大截面的惯性矩 – 越小 (内部的) 部分:

[数学] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [数学]
SkyCiv 为常见问题整理了方便的资源 转动惯量公式.
计算器
转动惯量的计算方法有很多种, 其中之一是使用软件使过程更容易.
SkyCiv版块生成器 是一款功能齐全的截面设计工具,其功能远远超出了转动惯量计算器的范围. 它还将向您展示如何找到转动惯量的逐步计算:
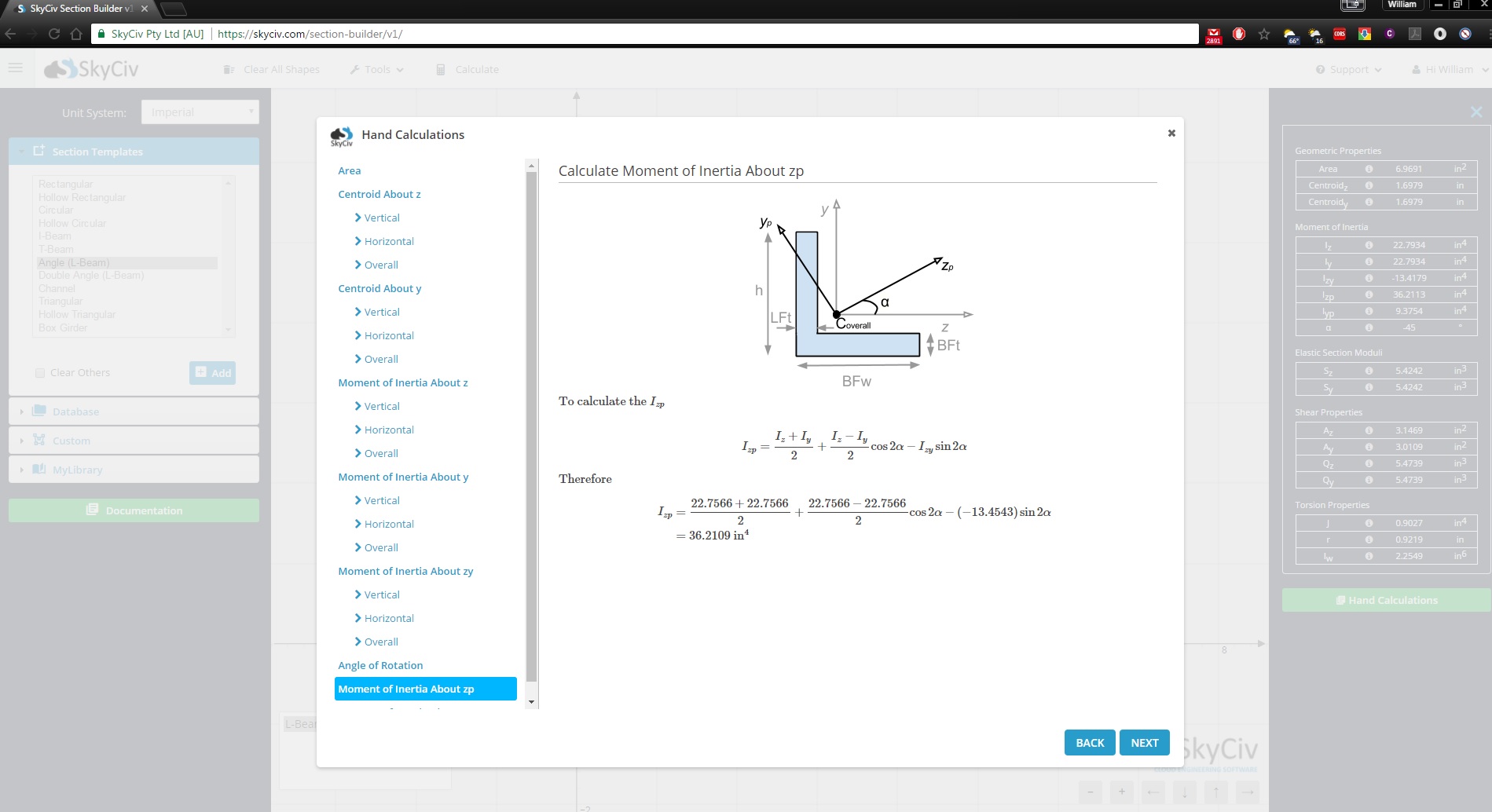
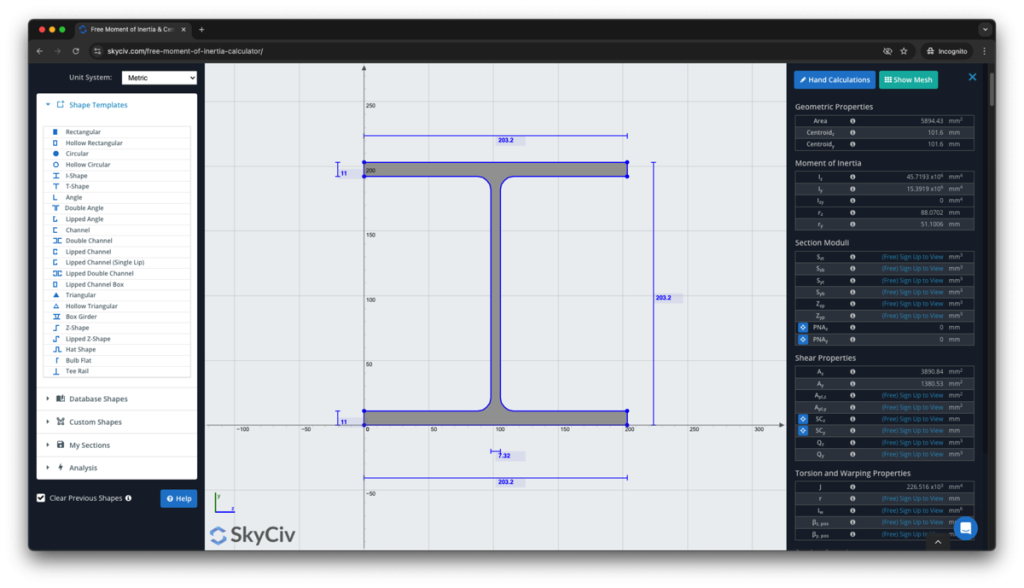
立即注册,探索有关 SkyCiv 软件的更多信息, 或预订 免费演示 为现有用户提供工程项目方面的帮助!
另外, SkyCiv有免费的 剖面属性计算器 作为快速设计库的一部分. 这是一个简化的工具, 但还将计算常见截面形状的转动惯量.
练习题
题 1: 矩形截面
问题: 计算转动惯量 (Ixx 和 Iyy) 对于具有宽度的矩形截面 (b) 的 200 毫米和高度 (H) 的 300 毫米.
解决方案: 矩形惯性矩的公式为:
替换给定值:
- b=200 mm
- 高=300 mm
对于 Ixx:
为了 Iyy:
题 2: 工字梁
问题: 计算主轴的转动惯量 (Ixx) 具有以下尺寸的工字梁截面:
- 上翼缘宽度 (TFw) = 6 在
- 顶部法兰厚度 (TFt) = 0.43 在
- 截面深度 = 6 在
- 腹板厚度 (Wt) = 0.29 在
- 底翼缘宽度 (高炉) = 6 在
- 底部法兰厚度 (高炉) = 0.43 在
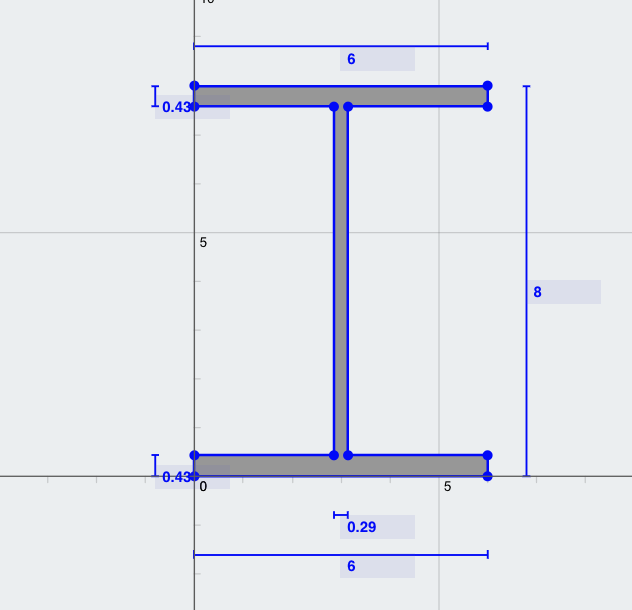
解决方案:


