目录
弯矩图计算
下面是关于如何计算弯矩图的简单说明 简支梁. 研究这种方法,因为它用途广泛 (并且可以适应许多不同类型的问题. 计算矩的能力 光束 对于结构工程师来说是一种非常普遍的做法,并且经常出现在大学和高中考试中. 早点注意就好, SkyCiv Beam 软件可以显示这些 手工计算 立即自动! 我们将按照今天的教程,以直接从 SkyCiv Beam 中的手计算模块中获取的示例为例.
首先, 什么是 弯矩Ť? 力矩是当力垂直于某个点以给定距离离开该点时发生的旋转力. 计算方法为垂直力乘以与点的距离. 弯矩只是由于瞬间在光束中发生的弯曲.
计算弯矩时要记住两件事,这一点很重要; (1) 标准单位为Nm和 (2) 当顶部纤维被压缩时, 弯曲被认为是正的. 有了定义, 让我们看一下计算弯矩图的步骤!
手工计算弯矩图
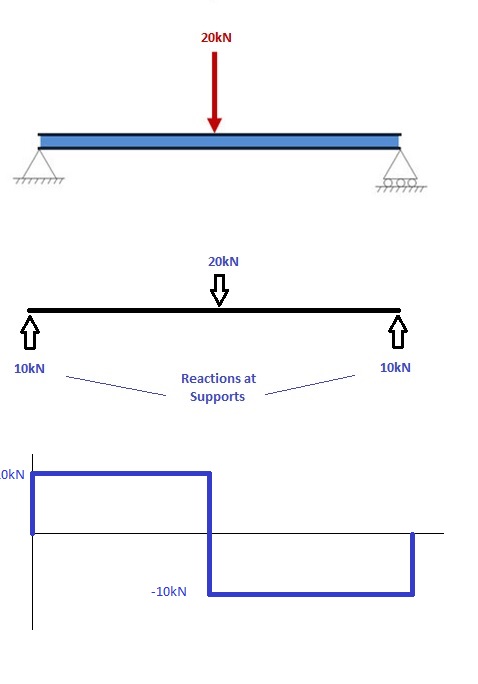
1. 计算支撑处的反应并绘制自由身图 (FBD)
如果您不确定如何 确定支撑处的反应 – 请先参阅本教程. 一旦你有反应, 画出你的自由身图 剪力图 在梁下. 最终计算力矩可以通过以下步骤完成:
2. 从左到右, 使 “削减” 每个反应/负载之前和之后
计算梁的弯矩, 我们必须以与剪力图相同的方式工作. 从x =开始 0 我们将横越梁并计算每个点的弯矩.
切 1
做一个 “切” 在光束的第一反应之后. 在我们的简单示例中:
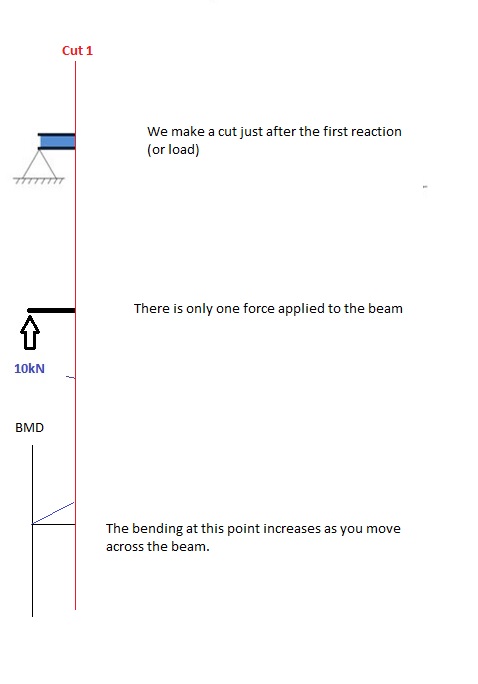

[资源: SkyCiv 梁手计算模块]
切 2
刚好在沿梁施加第二个力之前进行切割. 由于在第一次切割和第二次切割之间没有施加其他载荷, 的 弯矩方程 将保持不变. 这意味着我们可以计算最大弯矩 (在这种情况下,在中点, 或x = 5) 通过简单地将x = 5代入上式:
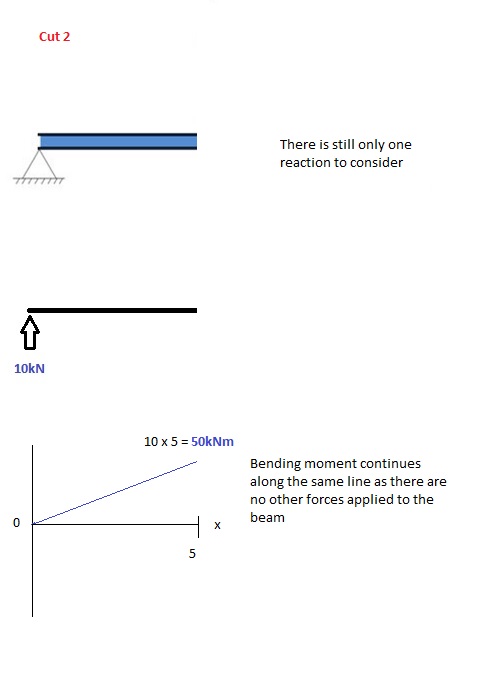
切 3
沿梁的第二个力刚好进行切割. 现在,我们有两个作用在切割点左侧的力: 10kN的支撑反应和-20kN的向下作用载荷. 因此,现在我们在沿着光束前进时必须考虑这两个力. 对于每一米,我们越过光束, 第一个力会增加+ 10kNm力矩,第二个力会增加-20kNm.
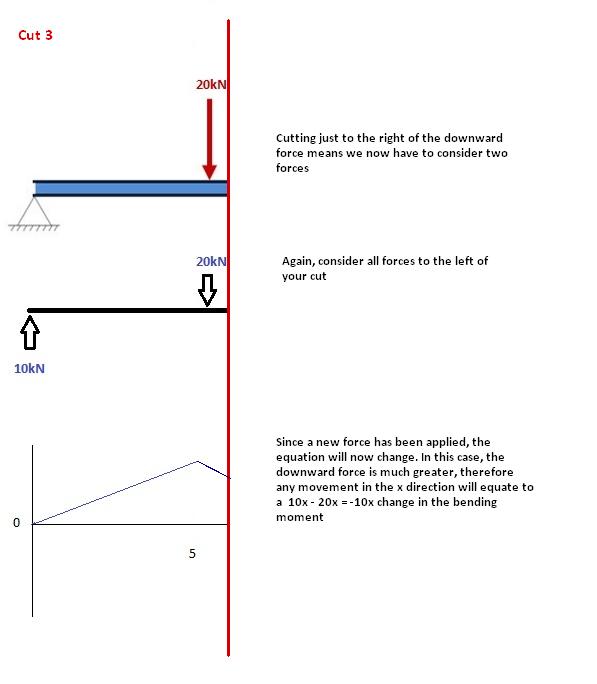
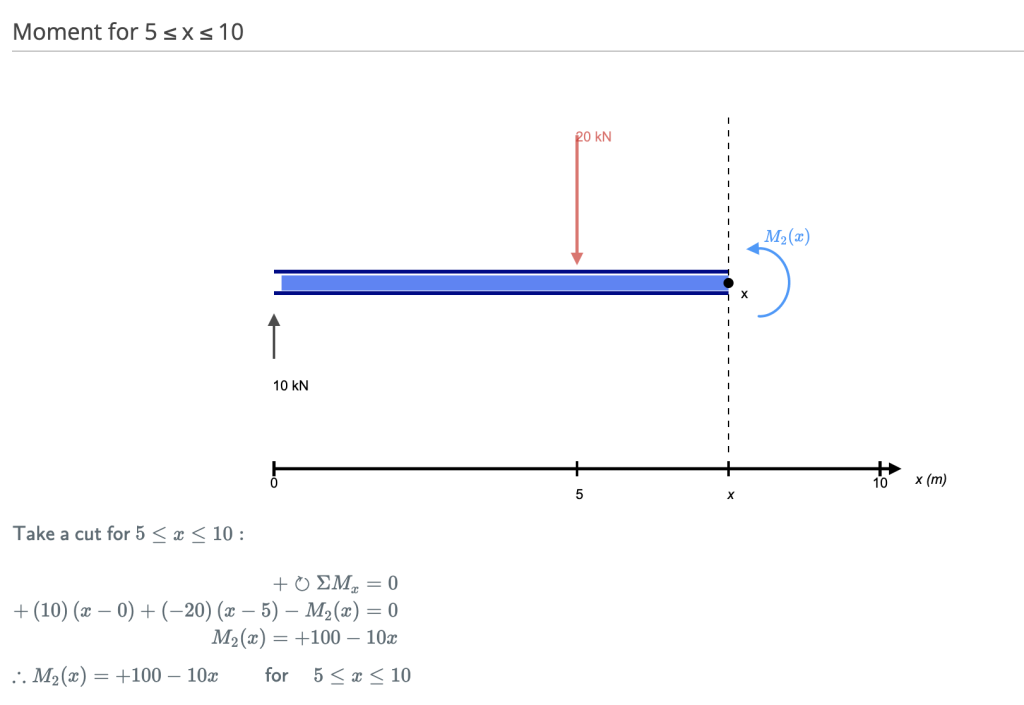
切 4
再次, 让我们越过梁的右侧并在下一个力之前进行切割. 在这种情况下, 我们的下一个削减将在Right Support做出反应之前发生. 因为支撑和我们之前的切割之间没有其他力量, 等式将保持不变: m(X) = 50 -10(x-5) 对于 5 ≤x≤ 10 让我们用x = 10代替它来找到梁末端的弯矩: m(X) = 50 – 10(10-5) = 0kNm这很合理. 由于我们的光束是静态的 (而且没有旋转) 当我们考虑所有力时,在这一点上我们的光束应该具有零力矩是有意义的. 它也满足我们的初始条件之一, 支撑力矩之和等于零. 注意: 如果您的计算使您得出除以下以外的任何其他数字 0, 你犯了一个错误!
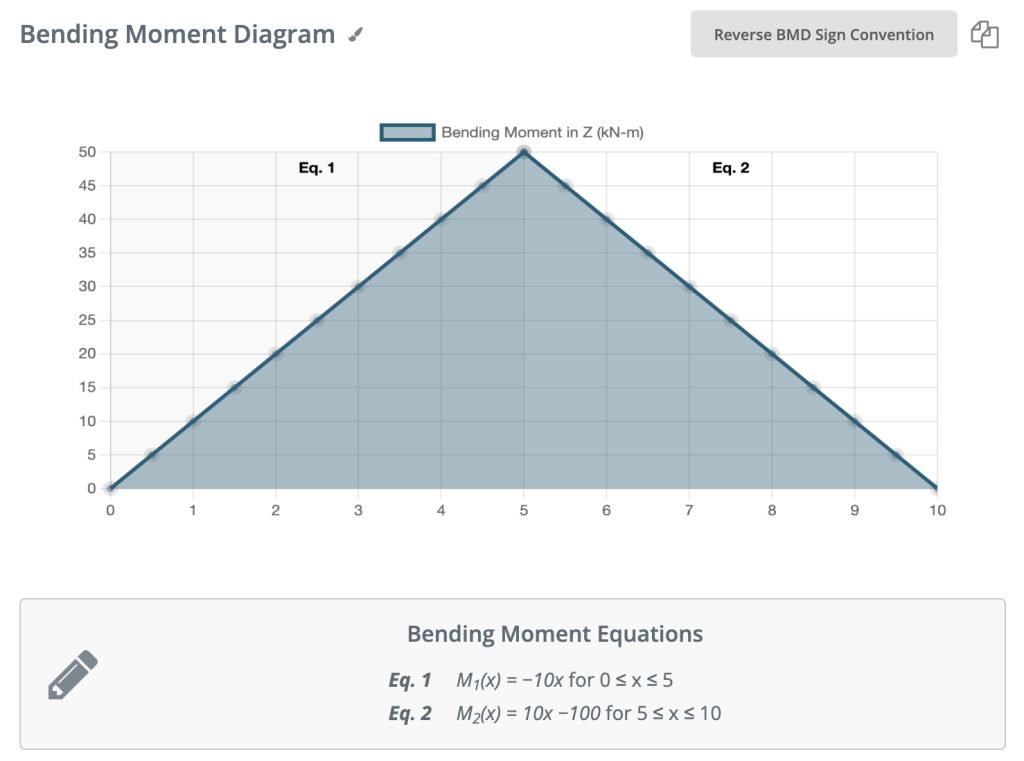
弯矩图的符号约定
我们在上面讨论了如何求弯矩. 当涉及到符号约定时,弯矩图可能会有些混乱. 根据来源,您可能会看到以相反方向绘制的相同图表. SkyCiv 使用的符号约定如下所示.
正弯矩:
如果弯矩为正, 光束的顶部光纤被压缩.

负弯矩:
如果弯矩为负, 梁的底部光纤被压缩.

这是计算弯矩图的指南, 如果您想了解有关此主题的更多信息, 访问我们的 梁教程 页. 在这里您可以找到许多其他有用的教程,例如 弯曲应力公式 要么 确定支撑处的反应.
奖金: 使用 SkyCiv Beam 计算弯矩
在我们的付费版本下 SkyCiv梁 计算器将向您显示完整的手工计算以及手工计算弯矩图所采取的步骤. 只需使用计算器为光束建模, 然后打解决. 它将向您展示如何绘制弯矩图的逐步计算 (包括削减).


