基础是结构的基本要素,通过将结构的总载荷传递和分配到地面来提供整体稳定性. 浅基础, 例如矩形或方形隔离基础, 与深基础相比,由于其结构简单且总体成本低,因此是首选的基础类型. 估计基础压力会极大地影响基础的设计和尺寸. 通常, 土体的许用承载力与基础下的控制基础压力之间的效用比是基础初始尺寸的依据. 一旦设置了初始基础尺寸, 进一步的安全性和稳定性设计检查, 如单向和双向剪切, 弯曲能力, 和开发长度检查, 根据使用的设计规范进行检查.
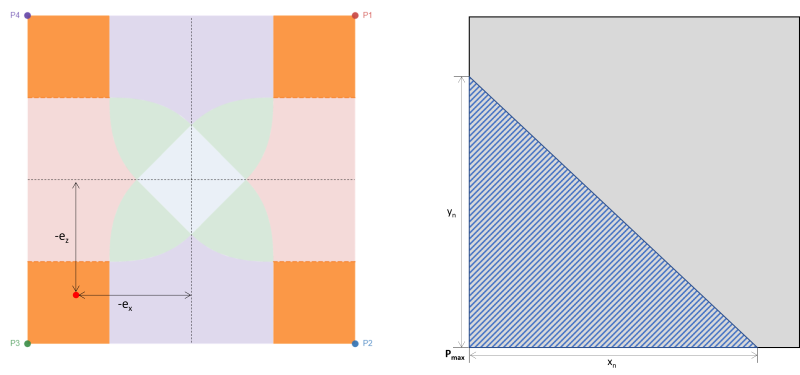
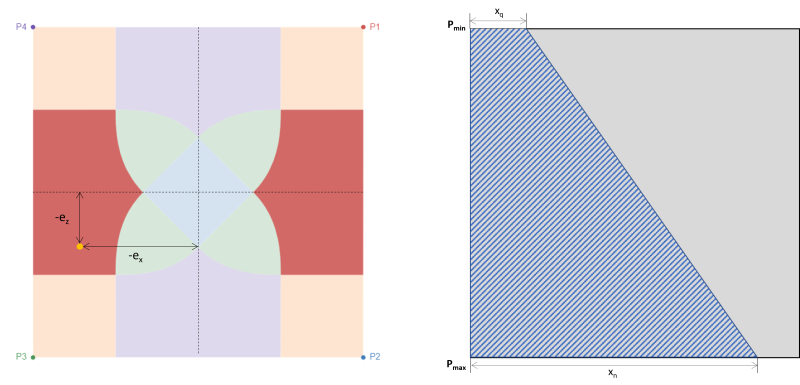
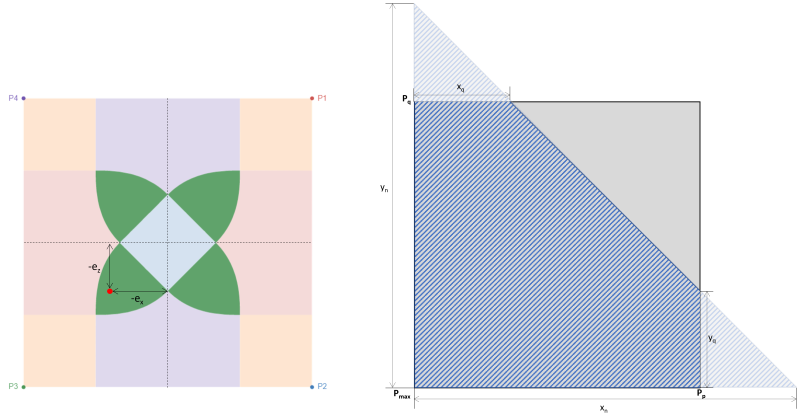
当基础受到双轴弯曲时 (中号X, 中号与), 假设轴向载荷 (P) 作用于偏心坐标 (ËX, Ë与) 有从中心旋转的趋势的地方. 土壤和基础之间的相互作用主要取决于基础尺寸和所施加载荷的偏心率. 取决于产生的偏心的位置, 基础压力导致基础完全或部分受压. 在实践中, 建议设计一个完全压缩的基础. 不应忽视土壤和基础之间的部分压缩或接触损失, 但由于计算复杂性,大多数设计者都会避免这种情况. 当产生的偏心率位于紧缩内或 C 区下方时,基础处于完全压缩状态. C区外的偏心使基础部分受压. 数字 1 在矩形基础上显示不同的指定区域.
本文重点讨论基于Bellos的不同区域分类下的角部压力计算 & 痕迹 (2017) 和SS. 雷的 (1995) 学习.
矩形基础的区域分类
矩形基础的区域分类源自不同作者的多项研究,旨在开发一种实用方法来估计预期载荷条件下的土压力分布. 如图 1, 有五个不同的地区 (A-E 区) 取决于产生偏心的位置. 每个区域对应不同的负载, 基础压力分布, 和变形. C区, 也称为内核, 是主要核心. 这是设计基础的理想区域, 导致基础完全受压. 该区域的尺寸相当于 1/6 其各自的基础长度.
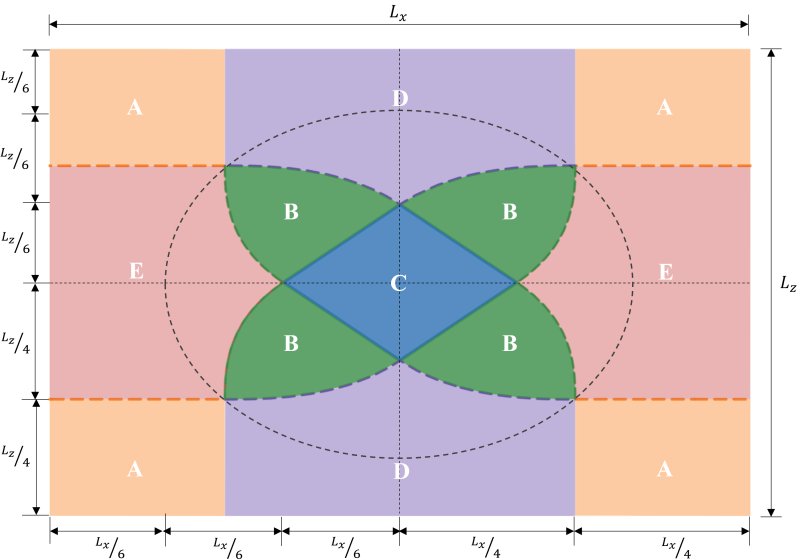
数字 1: 矩形基础的区域分类
次核心是椭圆区 (以图中虚线为界 1) 其长短半轴等于 1/3 其各自的基础长度. 该区域覆盖整个区域 B & C区及D区部分地区 & Ë. 次要核心导致基础部分压缩. 保持次要区域内的偏心距以获得可接受的基础设计是一种很好的做法.
超出次要区域的偏心是高双轴载荷的结果. 它覆盖了整个 A 区和 D 区的其余部分 & Ë. 建议避免在这些区域设计基础,因为它会有倾覆的风险. 因此, 建议重新设计此负载类型的基础尺寸.
下面列举求解各区域分类中的角压力的解析公式.
C区 (主要核心, 全压缩区)
如上所述, 这是设计基础时最优选的情况,因为它能够将基础的整个底座设置为压缩状态, 如图 2. 这种情况表现为紧距内有小偏心率或无偏心率. 数字 2 显示了紧缩内的偏心率以及拐角 P3 处的最大压力 & P4 和拐角处的最小压力 P1 & P2.
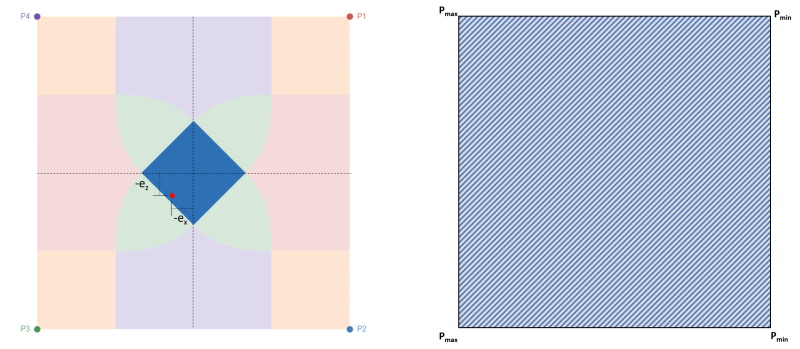
数字 2: 偏心 (-ËX, -Ë与) 在C区 & 全压缩区
最大 & 最小角压力 (美丽的 & 痕迹, 2017):
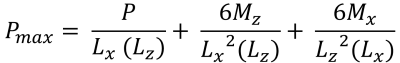
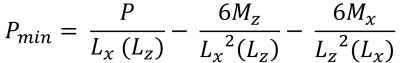
| 基于偏心率的角压力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| +ËX, +Ë与 | P最高 | P最高 | P分 | P分 |
| +ËX, -Ë与 | P最高 | P最高 | P分 | P分 |
| -ËX, -Ë与 | P分 | P分 | P最高 | P最高 |
| -ËX, +Ë与 | P分 | P分 | P最高 | P最高 |
A区 (三角形压缩区)
本例对应于基础每个角的四个矩形区域. 通常发生在双轴偏心率较大的情况下, 在角落之一施加高三角形压缩区域, 如图中阴影区域所示 3. 其余的角与土壤失去接触. 因此, 这种情况不建议设计.
 数字 3: 偏心 (-ËX, -Ë与) 在A区 & P3周围的三角形压缩区域
数字 3: 偏心 (-ËX, -Ë与) 在A区 & P3周围的三角形压缩区域
最大压力 (美丽的 & 痕迹, 2017):
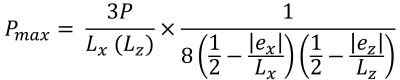
| 基于偏心率的角压力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ËX(+), Ë与(+) | P最高 | 0 | 0 | 0 |
| ËX(+), Ë与(-) | 0 | P最高 | 0 | 0 |
| ËX(-), Ë与(-) | 0 | 0 | P最高 | 0 |
| ËX(-), Ë与(+) | 0 | 0 | 0 | P最高 |
D区 (梯形压缩区)
D 区还对应于基础 x 方向附着区域的大偏心率, 如图 4. z 方向的偏心率 (Ë与) 远大于 x 方向 (ËX). 在这种情况下, 基础的两个角与土壤失去接触并产生梯形压缩区域. 与A区相比, 完全位于次要区域之外, D 区的一部分仍被次要区域覆盖.
数字 4: 偏心 (-ËX, -Ë与) 在D区 & P3周围梯形压缩区域
最大 & 最小角压力 (美丽的 & 痕迹, 2017):
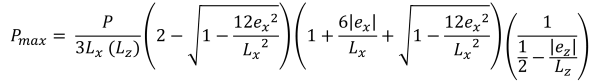
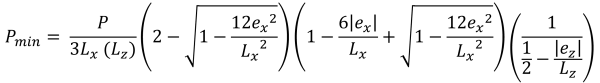
梯形受压区域的垂直高度 (美丽的 & 痕迹, 2017):
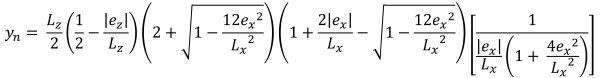
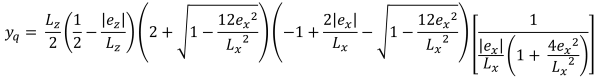
| 基于偏心率的角压力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ËX(+), Ë与(+) | P最高 | 0 | 0 | P分 |
| ËX(+), Ë与(-) | 0 | P最高 | P分 | 0 |
| ËX(-), Ë与(-) | 0 | P分 | P最高 | 0 |
| ËX(-), Ë与(+) | P分 | 0 | 0 | P最高 |
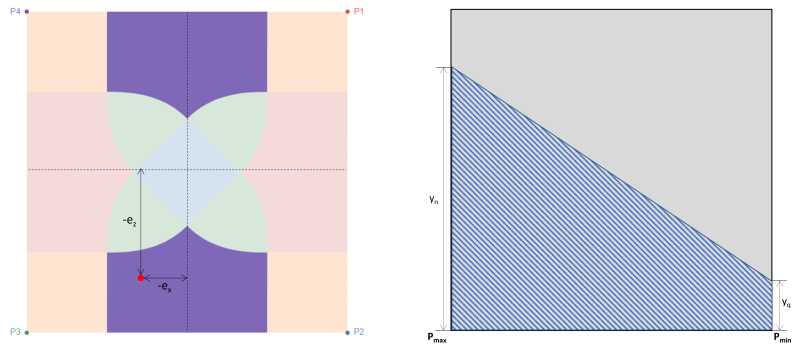
E区 (梯形压缩区)
与D区类似, 这种情况也会产生梯形压缩区域,但这是由 x 方向上的大偏心率引起的(ËX).
 数字 5: 偏心 (-ËX, -Ë与) 在E区 & P3周围梯形压缩区域
数字 5: 偏心 (-ËX, -Ë与) 在E区 & P3周围梯形压缩区域
最大 & 最小角压力 (美丽的 & 痕迹, 2017):
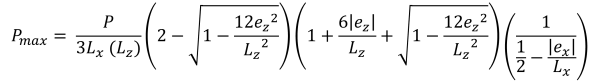
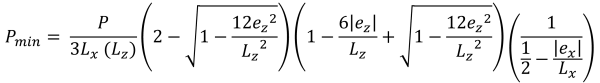
梯形压缩区域的水平底 (美丽的 & 痕迹, 2017):
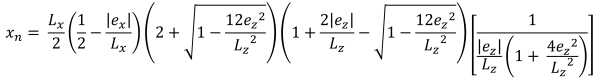
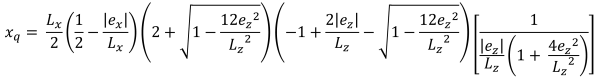
| 基于偏心率的角压力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ËX(+), Ë与(+) | P最高 | P分 | 0 | 0 |
| ËX(+), Ë与(-) | P分 | P最高 | 0 | 0 |
| ËX(-), Ë与(-) | 0 | 0 | P最高 | P分 |
| ËX(-), Ë与(+) | 0 | 0 | P分 | P最高 |
B区 (五边形压缩区)
当施加在基础上的载荷在次要区域内产生适度的偏心时,就会发生这种情况. B 区覆盖的区域以 C 区外部的两个弯曲侧面和一个平坦底座为界. 在这种情况下, 产生五边形压缩区域, 只有地脚的一角与土壤失去接触. 然而, 下面提供的解决方案稍微复杂,需要角点压力和 x 的数值求解方法 & 压缩区域的 y 截距.
拐角压力 (美丽的 & 痕迹, 2017):
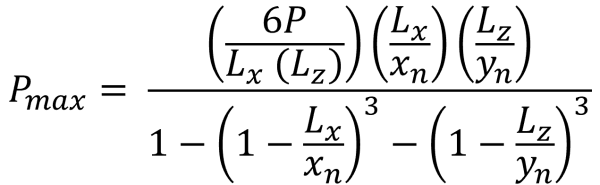
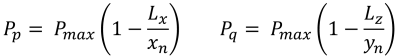
压缩区域的五边形边 (美丽的 & 痕迹, 2017):
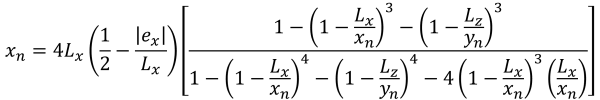
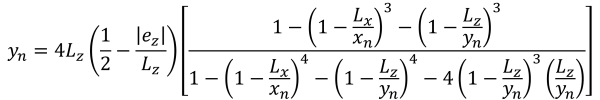

| 基于偏心率的角压力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| ËX(+), Ë与(+) | P最高 | Pq | 0 | Pp |
| ËX(+), Ë与(-) | Pp | P最高 | Pq | 0 |
| ËX(-), Ë与(-) | 0 | Pp | P最高 | Pq |
| ËX(-), Ë与(+) | Pq | 0 | Pp | P最高 |
或者, S.S 更直接的解决方案. 射线 (1995) 可用于五边形压缩区的角压力和截距. 方程如下:
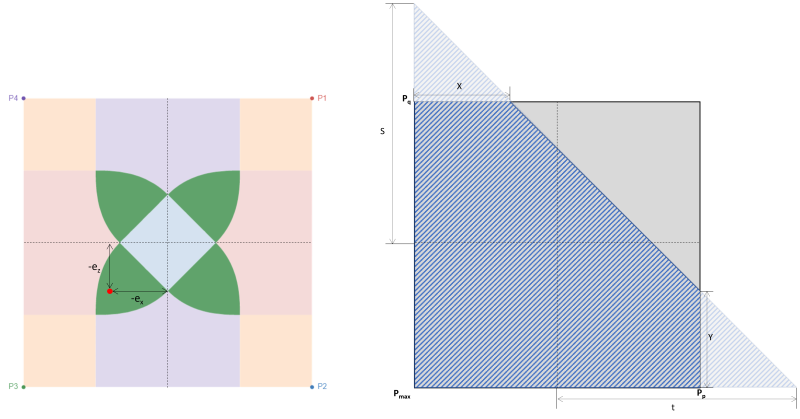
拐角压力 (SS. 射线, 1995):
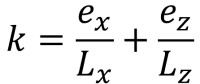


压缩区域的五边形边 (SS. 射线, 1995):
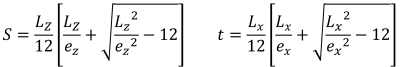
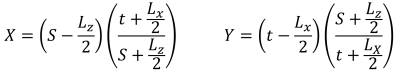
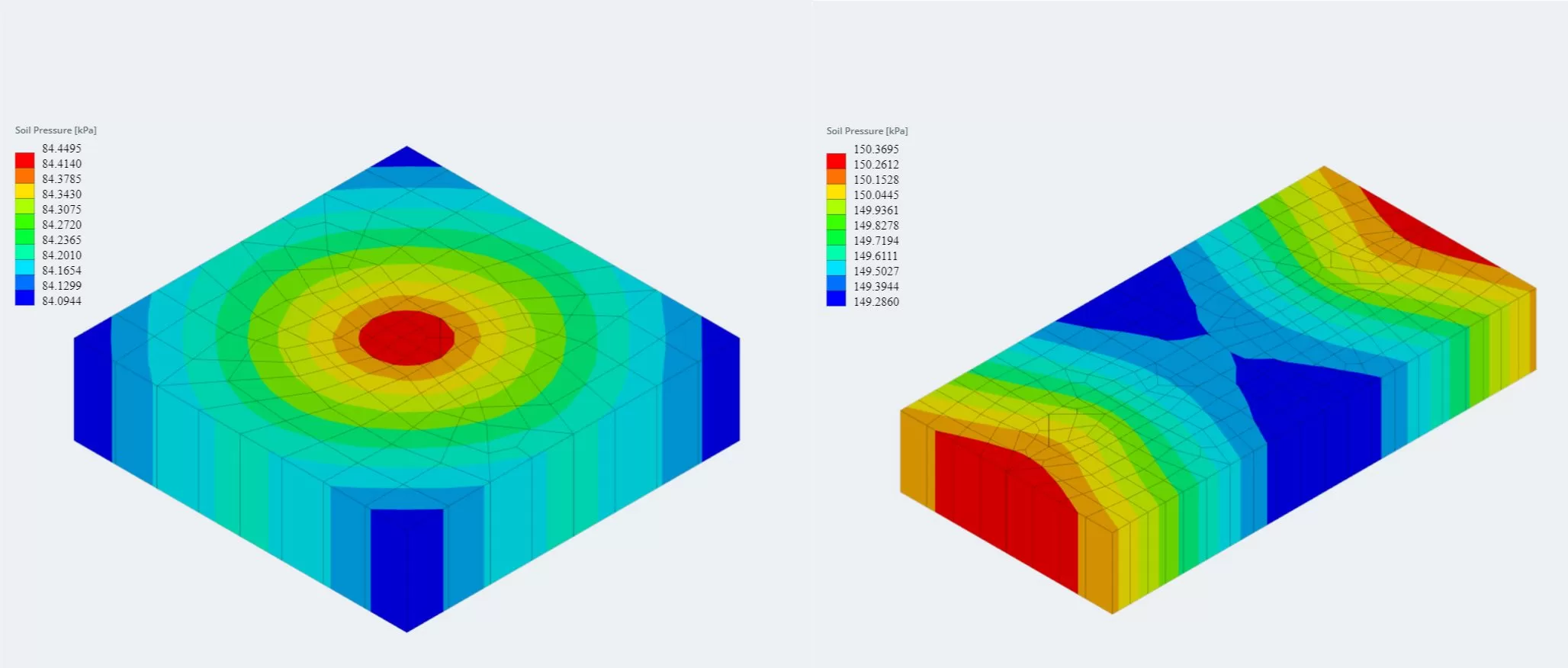
SkyCiv的 基础设计模块 能够求解矩形混凝土基础的基础压力. 根据不同的设计规范进行额外的设计检查 (ACI 318-14, 澳大利亚标准 2009 & 2018, 欧洲规范, 和加拿大标准) 也可用.
最新更新
最新版本的基础模块现已与有限元分析集成 (丑陋), 它提供了更强大的土壤压力分析,并引入了木臂分析以用于更详细的弯曲检查. 土壤压力和木臂力矩的 FEA 结果可以 3D 形式查看并添加到报告中.
想要试用SkyCiv的Foundation Design软件? 我们的免费工具允许用户执行 混凝土基础计算 无需任何下载或安装!
参考资料:
- 美丽的, J。, 痕迹, ñ. (2017). 刚性矩形扩展基础下线性土压力分布的完整分析解决方案.
- 计算极限承载能力, 计算极限承载能力. (2007). 计算极限承载能力 (7第版). 计算极限承载能力
- 拉瓦特, S。, 等. 阿尔. (2020). 双轴弯曲下的孤立矩形基础: 批判性评估和简化分析方法.
- 射线, SS. (1995). 钢筋混凝土. 布莱克威尔科学
产品开发人员
理学士 (民用), 理学硕士 (民用)
领英


