您的SkyCiv软件指南 - 教程, 使用指南和技术文章

各种梁截面的质心方程

质心的基础

需要注意的是，在横截面上, 整个区域面积均匀, 质心可以通过将相对于任意设置的轴的力矩之和求出, 但通常设置在顶部或底部光纤. 查看我们之前的文章计算梁截面的质心和 SkyCiv 免费质心计算器.

从根本上, 质心可以通过将面积总和上的矩求和来获得. 用这种方式表示.

[数学]
\酒吧{X}= 分数{1}{一个}\int xf left ( x 右 )dx
[数学]

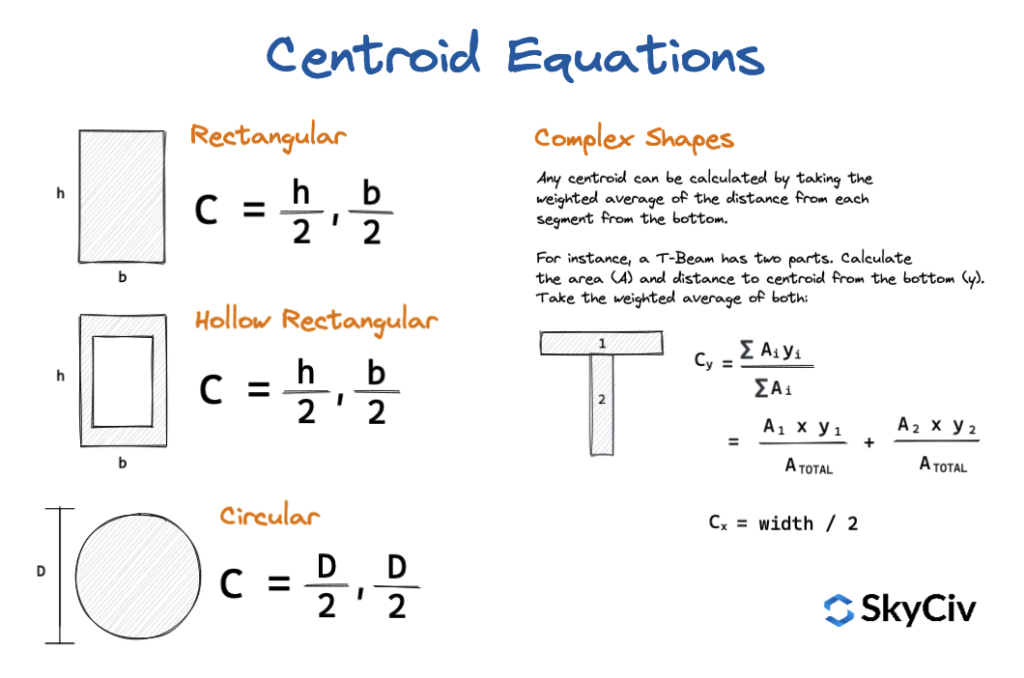
质心方程总结

在上式中, F(X) 是函数，x是力矩臂. 为了更好地说明这一点, 我们将推导其底与x轴重合的任意三角形的y重心. 在这种情况下, 三角形的形状, 是否平等, 等腰或斜角无关紧要，因为一切都只相对于x轴. 请注意，如果三角形的底边与轴重合或平行，则形状无关紧要. 求解x重心时情况并非如此. 代替, 您可以想象它是相对于y轴获得两个直角三角形的质心. 为了方便起见, 让我们想象一个等腰三角形类似于下面的参考表. 找到 b 和 h 之间的关系将得出以下关系.

[数学]
\压裂{-和}{X}= 分数{-H}{b}
[数学]

注意，当我们想象三角形是直立的时，斜率是负的. 如果我们想象三角形是倒置的, 斜率是正的. 而不管, 关系保持不变. 当x = f(和), 上面的关系可以改写如下.

[数学]
x = f 左 ( y 对 )= 分数{b}{H}和
[数学]

我们现在可以解决质心. 调整上面的第一个方程, 我们得到以下.

[数学]
\酒吧{和}= 分数{1}{一个}\int yf left ( y 对 )二
[数学]

插入其他值并替换上面的关系将得出以下公式.

[数学]
\酒吧{和}= 分数{2}{h}\int_{0}^{H} \压裂{b}{H}和^{2}二
[数学]

简化,

[数学]
\酒吧{和}= 分数{2}{h ^{2}}\剩下 [ \压裂{和^{3}}{3} \对 ]_{0}^{H}
[数学]
[数学]
\酒吧{和}= 分数{2}{h ^{2}}\剩下 [ \压裂{h ^{3}}{3}-0 \对 ]
[数学]
[数学]
\酒吧{和}= 分数{2}{3}H
[数学]

请注意，此解决方案取自顶部. 那么从底部截取的质心必须等于 1/3 的h.

常见形状和梁截面的质心公式

下面是一个列表各种梁截面形状以及到截面质心的距离. 这些方程式说明如何从截面的底部或最左端找到特定截面的质心. 对于SkyCiv Student和Structural订阅, 此参考也可以下载为PDF参考，以便随身携带. 梁截面的质心非常重要，因为它们定位中性轴，并且是分析梁截面时所需的最早步骤之一.

SkyCiv 还提供全面的截面摘要表，其中包含与梁截面有关的所有方程式和公式 (惯性矩, 地区等…).

下面列出了各种质心的方程式:

矩形或矩形截面的质心
参考	C_和 (距底的距离)	C_X (距最左点的距离)
	[数学] \dfrac{H}{2} [数学]	[数学] \dfrac{b}{2} [数学]
空心矩形截面的质心
	[数学] \dfrac{b}{2} [数学]	[数学] \dfrac{H}{2} [数学]
圆形或圆形截面的质心
	[数学] \dfrac{d}{2} [数学]	[数学] \dfrac{d}{2} [数学]
空心圆截面的质心方程
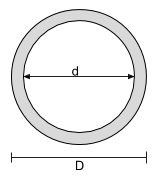	[数学] \dfrac{d}{2} [数学]	[数学] \dfrac{d}{2} [数学]
等腰三角形的质心
	[数学] \dfrac{H}{3} [数学]	[数学] \dfrac{b}{2} [数学]
工字梁的质心
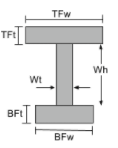	[数学] \压裂{TFw times TFt times left ( 高炉 + 瓦 + \压裂{TFt}{2} \对 )}{TFw 次TFt + Wt /次Wh + BFw 倍BFt} + [数学] [数学] \压裂{Wt timesWh times left ( 高炉 + \压裂{瓦}{2} \对 )}{TFw 次TFt + Wt /次Wh + BFw 倍BFt} + [数学] [数学] \压裂{BFw times BFt times left ( \压裂{高炉}{2} \对 )}{TFw 次TFt + Wt /次Wh + BFw 倍BFt} [数学]	[数学] TFw > 高炉, \压裂{TFw}{2}[数学] [数学] 高炉 > TFw, \压裂{高炉}{2} [数学]
T型截面的质心
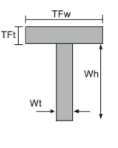	[数学] \压裂{Wt timesWh times left ( \压裂{瓦}{2} \对 )}{TFw 次TFt + Wt /次Wh } + [数学] [数学] \压裂{TFw times TFt times left ( 瓦 + \压裂{TFt}{2} \对 ) }{TFw 次TFt + Wt /次Wh } [数学]	[数学] \压裂{TFw}{2} [数学]
C部分的质心
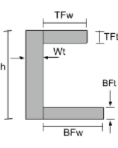	[数学] \压裂{TFw times TFt times left ( H – \压裂{TFt}{2} \对 )}{TFw 次TFt + Wt /次Wh + BFw 倍BFt} + [数学] [数学] \压裂{Wt times times left ( \压裂{H}{2} \对 )}{TFw 次TFt + Wt /次Wh + BFw 倍BFt} + [数学] [数学] \压裂{BFw times BFt times left ( \压裂{高炉}{2} \对 )}{TFw 次TFt + Wt /次Wh + BFw 倍BFt} [数学]	[数学] \压裂{TFt times TFw times left ( Wt + \压裂{TFw}{2} \对 )}{TFt 次TFw + h 次Wt + BFt 乘以BFw} + [数学] [数学] \压裂{h times Wt times left ( \压裂{Wt}{2} \对 )}{TFt 次TFw + h 次Wt + BFt 乘以BFw} + [数学] [数学] \压裂{BFt times BFw times left ( Wt + \压裂{高炉}{2} \对 )}{TFt 次TFw + h 次Wt + BFt 乘以BFw} [数学]
角质心
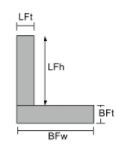	[数学] \压裂{LFt times LFh times left ( 高炉 + \压裂{低频}{2} \对 ) }{LFt 次LFh + BFw 倍BFt} + [数学] [数学] \压裂{BFw times BFt times left ( \压裂{高炉}{2} \对 )}{LFt 次LFh + BFw 倍BFt} [数学]	[数学] \压裂{LFh times LFt times left ( \压裂{低频}{2} \对 )}{LFh 次LFt + BFt 乘以BFw} + [数学] [数学] \压裂{BFt times BFw times left ( \压裂{高炉}{2} \对 )}{LFh 次LFt + BFt 乘以BFw} [数学]