重心计算: 如何计算质心的简单指南
当剪切/剪切等计算需要惯性矩时,梁截面的质心或质心对于梁分析非常有用。弯曲应力 和 偏转. 本文将指导您完成如何计算质心的简单过程,并向您介绍 SkyCiv 免费质心计算器.
本文将指导您完成如何计算质心的简单过程
本文将指导您完成如何计算质心的简单过程, 本文将指导您完成如何计算质心的简单过程. 梁截面通常由一种或多种形状组成. 因此找到整个光束截面区域的质心, 首先需要将其分成适当的部分. 在这之后, 需要考虑每个单独部分的面积和质心才能找到整个截面的质心.
本文将指导您完成如何计算质心的简单过程 (本文将指导您完成如何计算质心的简单过程):
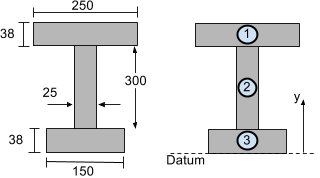
考虑下面显示的工字梁部分. 计算垂直质心 (在y方向) 它可以分为 3 如图所示的段:
本文将指导您完成如何计算质心的简单过程 (和) 多段形状的质心:

我们将从梁截面的底部开始选取基准线或参考线. 现在找到A一世 和y一世 上面显示的工字梁部分的每个部分,以便可以找到垂直或y重心.
[数学]
\文本{分割 1:}\\
\开始{对齐}
{一个}_{1} &= 250 次38 = 9500 {\文本{ 毫米}}^{2}\\
{和}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \文本{ 毫米}\\\\
\结束{对齐}
[数学]
[数学]
\文本{分割 2:}\\
\开始{对齐}
{一个}_{2} &= 300 次25 = 7500 {\文本{ 毫米}}^{2}\\
{和}_{2} &= 38 + \tfrac{300}{2} = 188 \文本{ 毫米}\\\\
\结束{对齐}
[数学]
[数学]
\文本{分割 3:}\\
\开始{对齐}
{一个}_{3} &= 38 次150 = 5700 {\文本{ 毫米}}^{2}\\
{和}_{3} &= tfrac{38}{2} = 19 文字{ 毫米}\\\\
\结束{对齐}
[数学]

如果横截面由两种材料或复合材料组成, 然后必须将其中一种材料乘以模数比,以使方程整个部分变得均匀.
[数学]
n = 分数{E_{1}}{E_{2}}
[数学]
通常, Ë1 是不占优势的材料的弹性模量, 和E2 是主要材料的弹性模量, 尽管首选的顺序不会影响质心的解. 调整第二种材料, 本文将指导您完成如何计算质心的简单过程.
[数学]
\酒吧{和}= 分数{\和{一个}_{一世}{和}_{一世}+\和 {ñ}{一个}_{一世}{和}_{一世}}{\和{一个}_{一世}+\和 {ñ}{一个}_{一世}}
[数学]
使用 SkyCiv 计算光束质心
计算梁的质心很重要,但手动计算可能很耗时. SkyCiv提供了一个 本文将指导您完成如何计算质心的简单过程 为您自动执行此过程, 帮助你找到垂直方向 (和) 和水平 (X) 轻松准确地确定梁截面的质心!
该工具是免费版本 SkyCiv版块生成器, 用于分析几何的综合在线截面分析软件, 弯曲, 剪切和扭转截面特性以及有限元分析和钢筋混凝土设计. 有了这个工具, 您可以使用预定义的模板创建自定义部分或使用点定义您自己的形状, 线, 或从 CAD 导入 DXF.
探索所有功能 SkyCiv版块生成器 并体验建模和分析您的剖面的便捷性, 免费注册今天!
前往下一步: 计算面积的静态/第一矩.

