在这篇文章中, 我们将使用最新版本的 ACI-318-19 开发板设计示例: “结构混凝土的建筑规范要求,” 包括 SkyCiv 中钢筋混凝土低层建筑的建模,重点是通过 ACI 认可的方法对软件结果和手工计算进行比较: “板的直接设计方法。” 该程序包括通过方便的因素将总弯矩分配到沿建筑物主方向和框架的不同条带中,以确定钢筋的数量和板中的位置.
我们希望您已阅读上一篇文章, S3D 板设计, 介绍自己如何使用 SkyCiv 进行建模和设计板. 我们建议您考虑的另一条有用的信息位于 如何对板进行建模? 阅读完这两篇文档后, 请随意深入研究以下完整的板比较示例!
建筑总体布局
下图显示了要计算的示例的等轴测视图和平面尺寸. 该建筑有两块高架平板,柱支撑之间没有横梁.
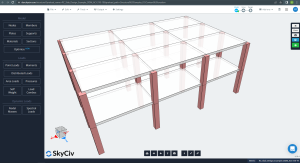
数字 1. 建筑示例的等距视图
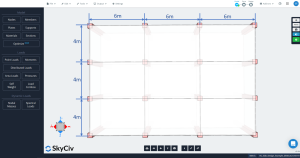
数字 2. 楼板平面尺寸
双向板的直接设计方法 (DDM)
局限性
ACI 318 允许使用 DDM 设计承受重力荷载的钢筋混凝土板, 根据几何形状收集一些必需品, 负荷关系, 对称, 等等. 我们可以在下面的列表中总结这些限制 (主成分分析注释):
- “每个方向必须有三个或更多的连续跨度。”: 数字 2 每个主方向显示三个跨度, 纵向和横向. 好的!
- “平板必须是矩形,长短跨度的比例 (支撑中心线到中心线) 不大于2。”: 据图 2, 该比率等于 \({\压裂{l_1}{4}= 分数{6米}{4米}=1.5 < 2}\). 好的!
- “连续跨度长度 (支撑中心线到中心线) 每个方向的差异不得超过 1/3 跨度较长的”. 每个方向的跨度长度相同, 6纵向 米,横向 4m. 好的!
- “列的偏移量不得超过 10% 跨度的 (在偏移方向) 从连续列的中心线之间的任一轴”. 建筑示例中没有柱偏移. 好的!
- “载荷必须均匀分布, 未分解或使用的活荷载不超过未分解或使用的恒载的两倍 (长径≤ 2)”. 获取每个重力载荷的值, 该比率定义为 \({\压裂{大号}{d}= 分数{2}{7.8}=0.256 < 2}\). 好的!.
- “对于双向梁支撑板, 梁在两个垂直方向上的相对刚度必须满足规范中给出的最小和最大要求。” 已经很满意了; 板中没有梁. 好的!
- “不允许通过代码重新分配负矩。” 由于示例简单, 无需重新分配板中的负力矩. 好的!.
纵向和横向条带定义
DDM 中的板必须分为两个主要条带,以便分析和设计特定的线网格: 列和中间条. 柱条的宽度是以下较小者 \({\压裂 {l_1}{4}}\) 和 \({\压裂{l_2}{4}}\), 哪里 \({l_1}\) 是沿线网格的跨度长度, \({l_2}\) 是垂直方向的横向长度.
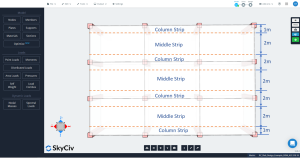
数字 3. 纵柱及中间条.
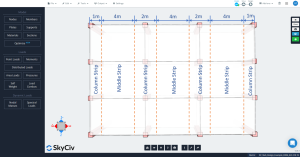
数字 4. 横柱及中间条.
最小厚度
ACI-318 建议使用以下公式: \({t_{分}}= {\压裂{l_n}{30}}={\压裂{6米-0.50米}{30}}=0.1833m = 0.20m\)
初步剪切强度检查
计算钢筋配筋前, 建议检查板的抗剪承载力, 一个用于连接中的直接剪力,另一个用于连接板柱上的冲剪能力.
计算剪切需求, 我们使用以下重力载荷:
- 自重板: \({SW={\伽玛_c}\次 {t_{平板}}={24 {\压裂{千牛}{米^3}}}\次 {0.20米}=4.8{\压裂{千牛}{米^2}} }\)
- 叠加恒载: \({标准差={3 {\压裂{千牛}{米^2}}}}\)
- 总静载 (短波+标清): \({D = {7.8 {\压裂{千牛}{米^2}}}}\)
- 活荷载 (住宅占用) : \({L={2 {\压裂{千牛}{米^2}}}}\)
- 分解强度负荷 (1.2深+1.6L): \({q_{ü}={12.56 {\压裂{千牛}{米^2}}}}\)
第一个剪切检查是 “梁剪” 类型, 其中下图表示获得总剪切力时需要考虑的区域. 我们检查每个方向, 占据更广阔的面积.
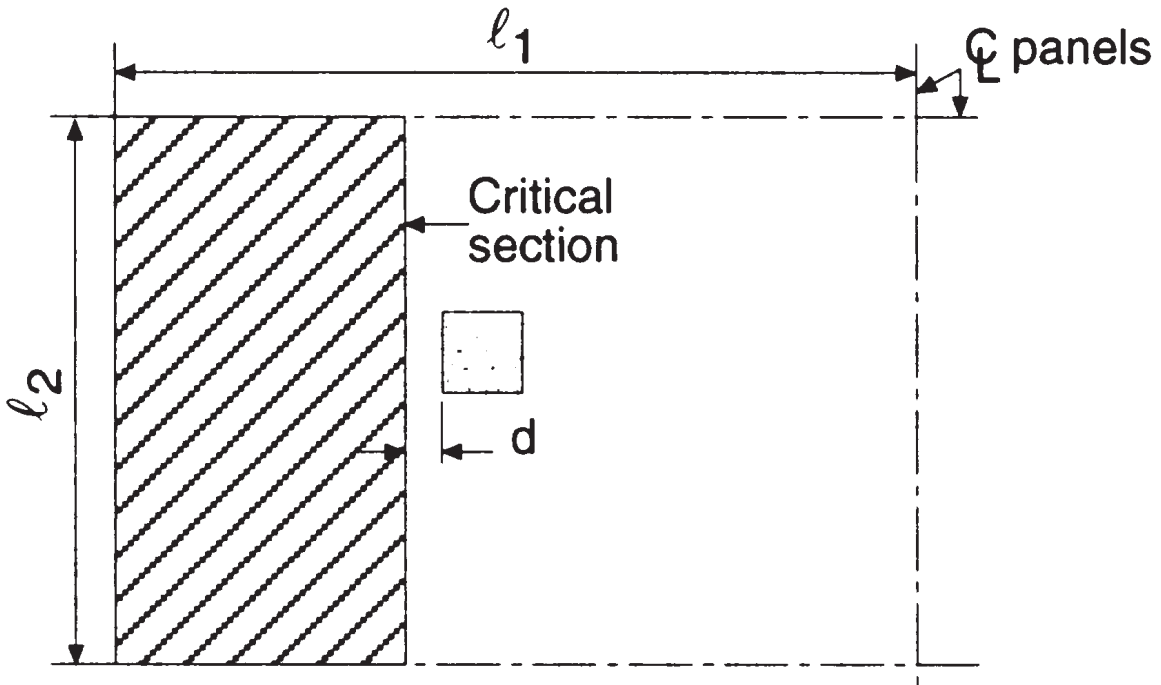
数字 5. 内柱梁剪 (Nadim Hassoun 和 Akthem AI-Manaseer, “结构混凝土理论与设计”)
在哪里:
- 纵向长度跨度, \({l_1 = 6.0m }\)
- 横向长度跨度, \({l_2 = 4.0m}\)
- 支流总面积, 纵向剪切 \({A_t = l_2 \times (\压裂{l_1}{2}-\压裂{c_1}{2}-d) = 4.0m \times (\压裂{6.0米}{2}-\压裂{0.50米}{2}-0.17米) = 10.32 米^2}\) (已选)
- 支流总面积, 横向剪切, \({A_t = l_1 \times (\压裂{l_2}{2}-\压裂{c_2}{2}-d) = 6.0m \times (\压裂{4.0米}{2}-\压裂{0.50米}{2}-0.17米) = 9.48 米^2}\)
- 方柱尺寸, \({c_1 = c_2 = 0.50m}\)
- 距离d, \({d = h_{平板} – 覆盖层 = 0.20m – 0.03米=0.17m }\)
因此, 内柱的最大梁剪力为
\({V_u =q_u\times A_t =12.56 {\压裂{千牛}{米^2}}\次 10.32 米^2 = 129.62 千牛 }\)
这将与剪切阻力进行比较, \({\phi_sV_c}\)
- 混凝土强度, \({f’_c = 25 兆帕}\)
- 钢筋屈服强度, \({f_y = 420 兆帕}\)
- \({\phi_s = 0.75}\)
- \({\phi_sV_c = 0.17\phi_s \lambda \sqrt(f'_c) 黑白; b_w=l_2}\)
\({\phi_sV_c = 0.17\times 0.75\times 1\times \sqrt(25 兆帕) \次 4000 mm\times 170 毫米= 433.50 千牛 }\)
我们可以看到剪切阻力大于剪切需求: \({\phi_sV_c = 433.50 千牛 > V_u = 129.62 千牛 }\) 好的!.
根据以下图片, 我们必须计算内部板柱连接处混凝土的冲切承载力和承受的力. 该规范检查冲剪的目的是保持低剪切应力值.
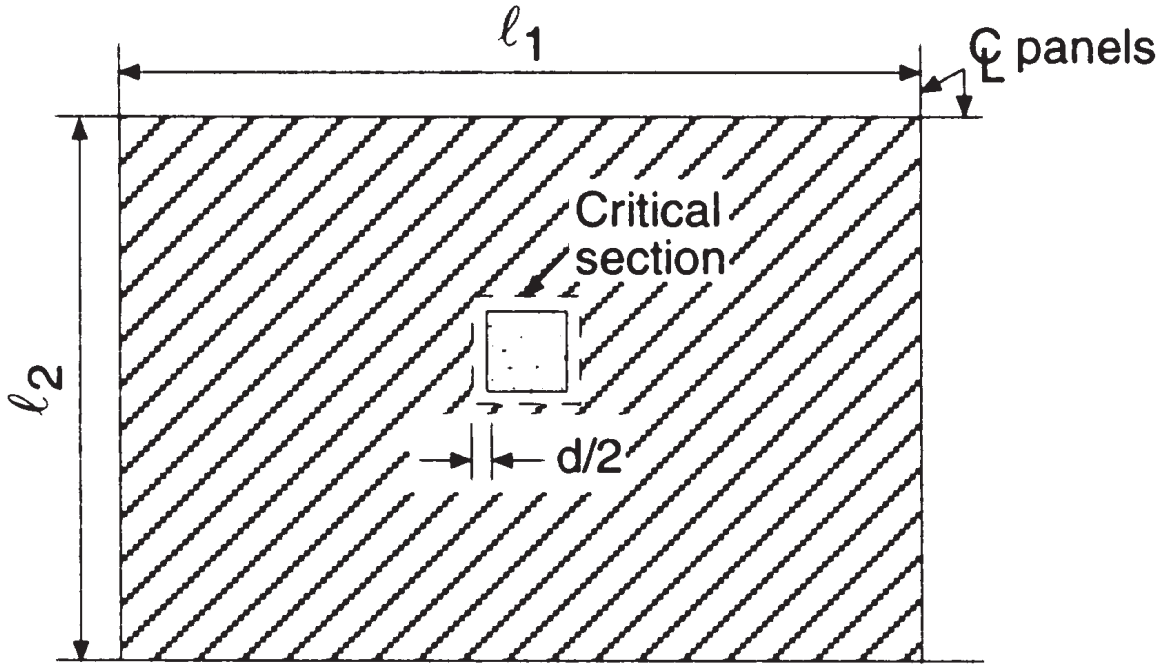
数字 6. 内柱双向剪力 (Nadim Hassoun 和 Akthem AI-Manaseer, “结构混凝土理论与设计”)
- 支流总面积, 冲剪机, \({A_t = l_1 \times l_2 – (c_1+d)^2 = 6.0m \times 4.0m – (0.50米+0.17m)可以假设为 23.55 米^2}\) (两个主要方向的面积相同)
需要抵抗的总剪切力为
\({V_u =q_u\times A_t =12.56 {\压裂{千牛}{米^2}}\次 23.55 米^2 = 295.79 千牛 }\)
获得双向板的冲剪能力, 我们将使用代码 ACI-318 建立的经验方法, 考虑了关键截面有效周长内可用的最大剪应力. 内柱更保守的表达式是
- 冲剪能力, \({\phi_sV_c = 0.33\phi_s \lambda \sqrt(f'_c) b_0 d; b_0=4\times (c_1+d)}\)
因此, 我们的抗剪强度为
\({\phi_sV_c = 0.33\times 0.75 \次 1 \sqrt(25 兆帕) \次 (4\次 (500 毫米+170毫米)\乘170毫米) = 563.81 千牛 }\)
我们可以看到剪切阻力大于剪切需求: \({\phi_sV_c = 563.81 千牛 > V_u = 295.75 千牛 }\) 好的!.
我们已经验证了内部连接处的一个和双向剪切需求. 由于这两个要求都小于其各自的能力或抵抗力, 现在,我们将移动以计算板弯曲的主要钢筋增强.
如果你是 SkyCiv 的新手, 自行注册并测试软件!
每跨度的总系数静力矩.
可以发展为双固定末端梁的最大力矩是等静力矩等于 \({M=frac{w\times {l_1}^ 2}{8}}\) (见图 6).
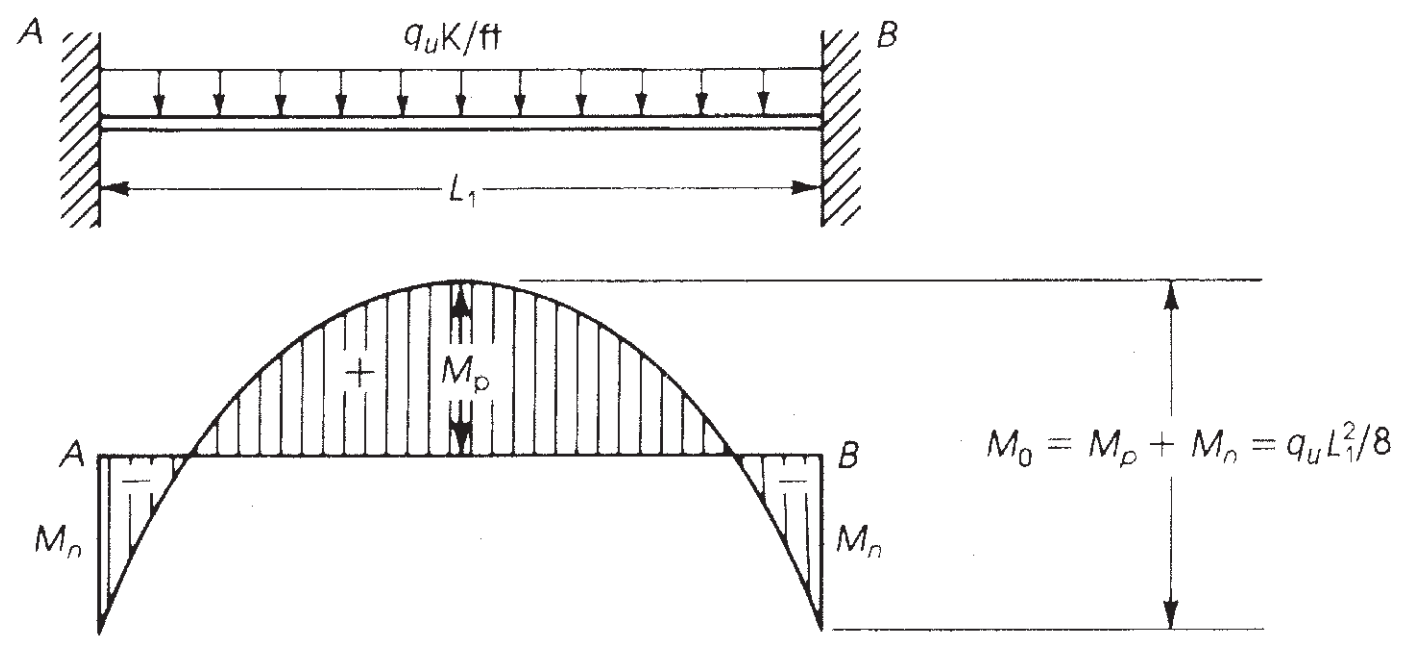
数字 7. 固定端梁的弯矩. (Nadim Hassoun 和 Akthem AI-Manaseer, “结构混凝土理论与设计”)
ACI-18 采用了这一原则并, 直接设计法 (DDM), 确定每个跨度要考虑的最大静态力矩 \({M_0}\)
纵向方向:
- \({M_0 = \frac {q_u\times l_2\times {由使用公式计算的最小值控制{ñ,1}}^ 2}{8}}\)
- \({M_0 = \frac {12.56 {\压裂{千牛}{米^2}}\times 4.0m\times (6米-0.50米)^ 2}{8}= 189.97 kn-m}\)
横向方向:
- \({M_0 = \frac {q_u\times l_1\times {由使用公式计算的最小值控制{ñ,2}}^ 2}{8}}\)
- \({M_0 = \frac {12.56 {\压裂{千牛}{米^2}}\times 6.0m\times (4米-0.50米)^ 2}{8}= 115.40 kN-m}\)
下一步是考虑面板类型来分配总力矩, 内部或外部. (见图 7). 在那之后, 由于跨度是连续的, 有必要将时刻分为积极时刻和消极时刻. 最后一个如图所示 8 和 9.
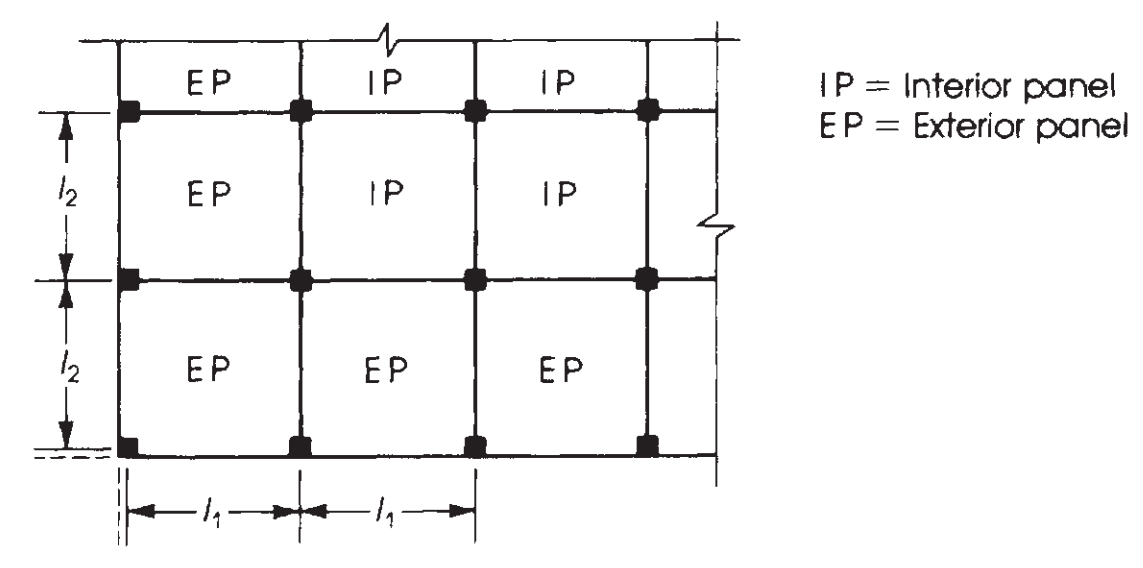
数字 8. 根据面板在楼板平面图中的相对位置定义面板. (Nadim Hassoun 和 Akthem AI-Manaseer, “结构混凝土理论与设计”)
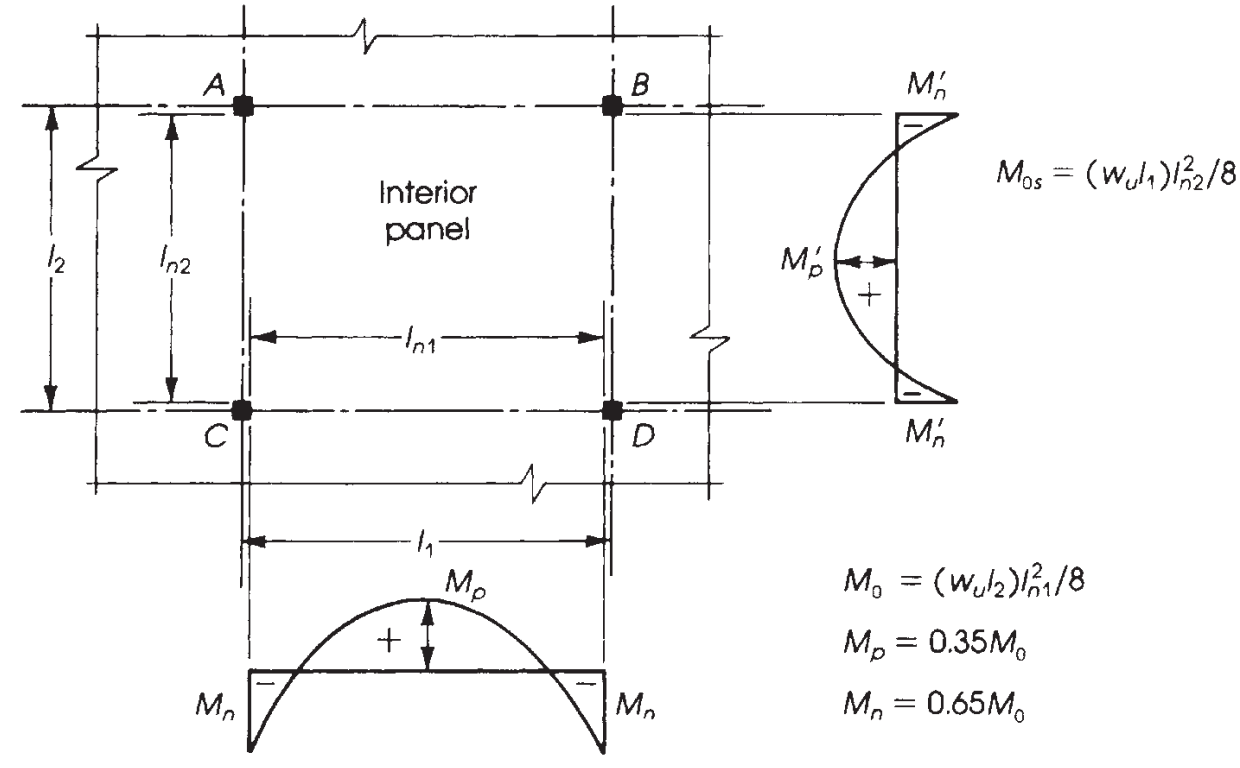
数字 9. 内板力矩分布. (Nadim Hassoun 和 Akthem AI-Manaseer, “结构混凝土理论与设计”)
根据我们正在设计的板,了解力矩的正确分布至关重要. 在这个例子中, 我们有下图中的最后一个案例 (数字 9), “无横梁,” 应用于没有任何梁的平板或实心板, 既不在边缘也不在支撑之间.
图中五种情况的主要区别 9 是分配给外部面板的力矩分数, 其中最后的相对约束改变了要计算的值.
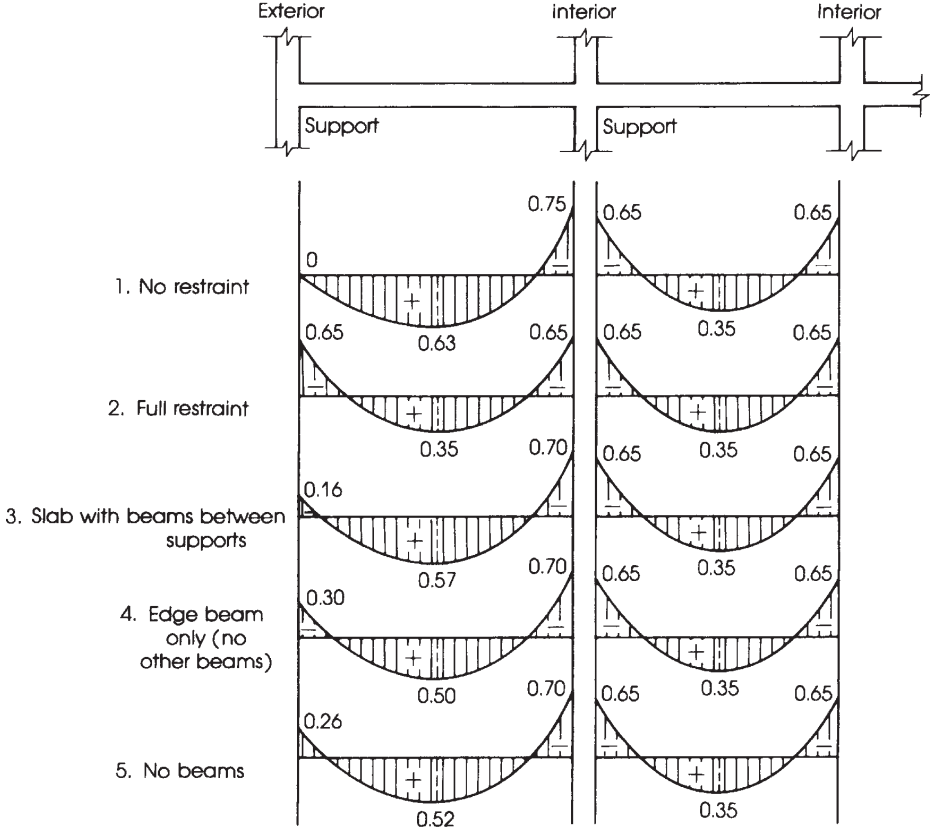
数字 10. 总静力矩分布为负跨距力矩和正跨距力矩. (Nadim Hassoun 和 Akthem AI-Manaseer, “结构混凝土理论与设计”)
总因子矩的分布 \({M_0}\) 每个跨度分为消极和积极的时刻.
一次 \({M_0}\) 已计算出, 是时候将每个设计条中的力矩分数分配为正和负, 那是, 列和中间条. 为了更清楚, 数字 10 帮助指定在总力矩分布中要考虑的适当因素.
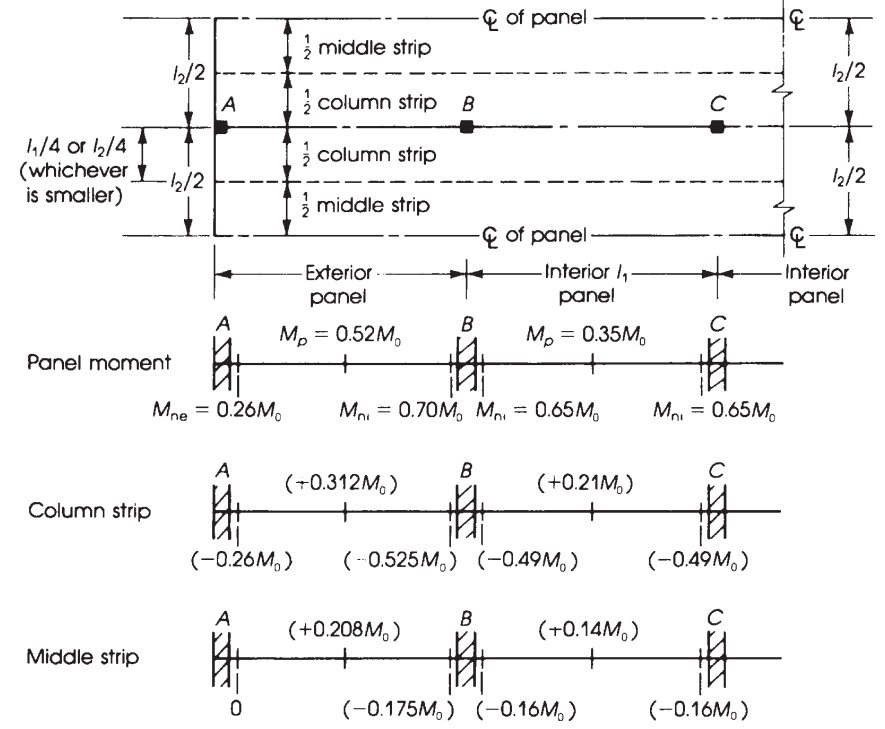
数字 11. 平板等效刚架宽度和力矩分布. (Nadim Hassoun 和 Akthem AI-Manaseer, “结构混凝土理论与设计”)
使用图中所示的先前因素 10, 我们在下表中得到最终时刻.
纵向方向: \({M_0= 189.97 千牛·米}\)
| 跨度 (ES:外部的, 是:内部的) | 总时刻 (千牛·米) | 柱条力矩 (千牛·米) | 中间带矩 (千牛·米) |
|---|---|---|---|
| 外部负ES | 0.26M0=49.39 | 0.26M0=49.39 | 0 |
| 正ES | 0.52M0=98.78 | 0.31M0=58.89 | 0.21M0=39.89 |
| 内部负ES | 0.70M0=132.98 | 0.53M0=100.68 | 0.17M0=32.29 |
| 正向IS | 0.35M0=66.49 | 0.21M0=39.89 | 0.14M0=26.60 |
| 负离子 | 0.65M0=123.48 | 0.49M0=93.09 | 0.16M0=30.40 |
曾经散发过的时刻, 是时候确定要放置在板中的钢筋了. 我们只会进行一次计算,然后将所有结果放入表格中.
柱条外部负跨距中的力矩, \({M_u = 49.39 千牛·米}\)
- 假设张力控制部分. \({\phi_f = 0.9}\)
- 柱条宽度, \({b=2.0m}\)
- 钢筋面积, \({A_s = \frac{亩}{\phi_f\times 0.9d\times fy}= frac{49.39千牛·米}{0.9\次 0.9(0.17米)\次 420 兆帕}=853.996 {毫米}^ 2}\)
- \({\o{分} = 0.0018}\). 钢材最小配筋面积, \({一个_{s,分}=\rho_{分}\times b\times d = 0.0018 \times 2.0m \times 0.17m =612 {毫米}^ 2}\). 现在, 检查该部分是否表现为张力控制.
- \({a = frac{A_s\times f_y}{0.85\times f’c\times b} = frac{853.996 {毫米}^2\times 420 兆帕}{0.85\次 25 MPa\times 2.0m }= 8.439 毫米}\)
- \({c = 压裂{一个}{\测试版_1}= 分数{8.439 毫米}{0.85} = 9.929mm }\)
- \({\变体_t = (\压裂{0.003}{C})\由使用公式计算的最小值控制 – 0.003 = (\压裂{0.003}{9.929毫米})\乘170毫米 – 0.003 = 0.048 > 0.005 }\) 好的!, 这是一个张力控制部分!.
| 跨度(ES:外部的, 是:内部的) | 柱条矩 (千牛·米) | \({一个_{s,计算} ({毫米}^ 2)}\) | \({一个_{s,分} ({毫米}^ 2)}\) | \({一个 (毫米)}\) | \({C (毫米)}\) | \({\变体_t > 0.005}\) |
|---|---|---|---|---|---|---|
| 外部负ES | 49.39 | 853.996 | 612.0 | 8.439 | 9.929 | 0.048 > 0.005! |
| 正ES | 58.89 | 1018.259 | 612.0 | 10.063 | 11.839 | 0.040 > 0.005! |
| 内部负ES | 100.68 | 1740.844 | 612.0 | 17.204 | 20.24 | 0.022 > 0.005! |
| 正向IS | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.06 > 0.005! |
| 负离子 | 93.09 | 1609.607 | 612.0 | 15.907 | 18.714 | 0.024 > 0.005! |
中间条带外部正跨距的力矩, \({M_u = 39.89 千牛·米}\)
- 假设张力控制部分. \({\phi_f = 0.9}\)
- 中带宽度, \({b=2.0m}\)
- 钢筋面积, \({A_s = \frac{亩}{\phi_f\times 0.9d\times fy}= frac{39.89千牛·米}{0.9\次 0.9(0.17米)\次 420 兆帕}=689.733 {毫米}^ 2}\)
- \({\o{分} = 0.0018}\). 钢材最小配筋面积, \({一个_{s,分}=\rho_{分}\times b\times d = 0.0018 \times 2.0m \times 0.17m =612 {毫米}^ 2}\). 现在, 检查该部分是否表现为张力控制.
- \({a = frac{A_s\times f_y}{0.85\times f’c\times b} = frac{689.766 {毫米}^2\times 420 兆帕}{0.85\次 25 MPa\times 2.0m }= 6.816 毫米}\)
- \({c = 压裂{一个}{\测试版_1}= 分数{6.816 毫米}{0.85} = 8.019 毫米 }\)
- \({\变体_t = (\压裂{0.003}{C})\由使用公式计算的最小值控制 – 0.003 = (\压裂{0.003}{8.019毫米})\乘170毫米 – 0.003 = 0.0605 > 0.005 }\) 好的!, 这是一个张力控制部分!.
| 跨度(ES:外部的, 是:内部的) | 中条矩 (千牛·米) | \({一个_{s,计算} ({毫米}^ 2)}\) | \({一个_{s,分} ({毫米}^ 2)}\) | \({一个 (毫米)}\) | \({C (毫米)}\) | \({\变体_t > 0.005}\) |
|---|---|---|---|---|---|---|
| 外部负ES | 0 | 0.00 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正ES | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.061 > 0.005! |
| 内部负ES | 32.29 | 558.322 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正向IS | 26.60 | 459.937 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| 负离子 | 30.40 | 525.642 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
横向方向: \({M_0= 115.40 千牛·米}\)
| 跨度 (ES:外部的, 是:内部的) | 总时刻 (千牛·米) | 柱条力矩 (千牛·米) | 中间带矩 (千牛·米) |
|---|---|---|---|
| 外部负ES | 0.26M0=30.00 | 0.26M0=30.00 | 0 |
| 正ES | 0.52M0=60.00 | 0.31M0=35.77 | 0.21M0=24.23 |
| 内部负ES | 0.70M0=80.78 | 0.53M0=61.16 | 0.17M0=19.62 |
| 正向IS | 0.35M0=40.39 | 0.21M0=24.23 | 0.14M0=16.16 |
| 负离子 | 0.65M0=75.01 | 0.49M0=56.55 | 0.16M0=18.46 |
曾经散发过的时刻, 是时候确定要放置在板中的钢筋了. 我们只会进行一次计算,然后将所有结果放入表格中.
柱条外部负跨距中的力矩, \({M_u = 30.00 千牛·米}\)
- 假设张力控制部分. \({\phi_f = 0.9}\)
- 柱条宽度, \({b=2.0m}\)
- 钢筋面积, \({A_s = \frac{亩}{\phi_f\times 0.9d\times fy}= frac{30.00千牛·米}{0.9\次 0.9(0.17米)\次 420 兆帕}=518.726 {毫米}^ 2}\)
- \({\o{分} = 0.0018}\). 钢材最小配筋面积, \({一个_{s,分}=\rho_{分}\times b\times d = 0.0018 \times 2.0m \times 0.17m =612 {毫米}^ 2}\). 现在, 检查该部分是否表现为张力控制.
- \({a = frac{A_s\times f_y}{0.85\times f’c\times b} = frac{518.726 {毫米}^2\times 420 兆帕}{0.85\次 25 MPa\times 2.0m }= 6.048 毫米}\)
- \({c = 压裂{一个}{\测试版_1}= 分数{6.048 毫米}{0.85} = 7.115毫米 }\)
- \({\变体_t = (\压裂{0.003}{C})\由使用公式计算的最小值控制 – 0.003 = (\压裂{0.003}{7.115毫米})\乘170毫米 – 0.003 = 0.069 > 0.005 }\) 好的!, 这是一个张力控制部分!.
| 跨度(ES:外部的, 是:内部的) | 柱条矩 (千牛·米) | \({一个_{s,计算} ({毫米}^ 2)}\) | \({一个_{s,分} ({毫米}^ 2)}\) | \({一个 (毫米)}\) | \({C (毫米)}\) | \({\变体_t > 0.005}\) |
|---|---|---|---|---|---|---|
| 外部负ES | 30.00 | 518.726 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正ES | 35.77 | 618.494 | 612.0 | 6.112 | 7.191 | 0.068 > 0.005! |
| 内部负ES | 61.16 | 1057.509 | 612.0 | 10.451 | 12.295 | 0.038 > 0.005! |
| 正向IS | 24.23 | 418.958 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| 负离子 | 56.55 | 977.799 | 612.0 | 9.663 | 11.368 | 0.042 > 0.005! |
中间条带外部正跨距的力矩, \({M_u = 24.23 千牛·米}\)
- 假设张力控制部分. \({\phi_f = 0.9}\)
- 柱条宽度, \({b=4.0m}\)
- 钢筋面积, \({A_s = \frac{亩}{\phi_f\times 0.9d\times fy}= frac{24.23 千牛·米}{0.9\次 0.9(0.17米)\次 420 兆帕}=418.958 {毫米}^ 2}\)
- \({\o{分} = 0.0018}\). 钢材最小配筋面积, \({一个_{s,分}=\rho_{分}\times b\times d = 0.0018 \times 4.0m \times 0.17m =1224 {毫米}^ 2}\). 现在, 检查该部分是否表现为张力控制.
- \({a = frac{A_s\times f_y}{0.85\times f’c\times b} = frac{1224 {毫米}^2\times 420 兆帕}{0.85\次 25 MPa\times 4.0m }= 6.048 毫米}\)
- \({c = 压裂{一个}{\测试版_1}= 分数{6.048 毫米}{0.85} = 7.115 毫米 }\)
- \({\变体_t = (\压裂{0.003}{C})\由使用公式计算的最小值控制 – 0.003 = (\压裂{0.003}{7.115毫米})\乘170毫米 – 0.003 = 0.069 > 0.005 }\) 好的!, 这是一个张力控制部分!.
| 跨度(ES:外部的, 是:内部的) | 中条矩 (千牛·米) | \({一个_{s,计算} ({毫米}^ 2)}\) | \({一个_{s,分} ({毫米}^ 2)}\) | \({一个 (毫米)}\) | \({C (毫米)}\) | \({\变体_t > 0.005}\) |
|---|---|---|---|---|---|---|
| 外部负ES | 0.00 | 0.00 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正ES | 24.23 | 418.958 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| 内部负ES | 19.62 | 339.247 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| 正向IS | 16.16 | 279.420 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| 负离子 | 18.46 | 319.189 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
如果你是 SkyCiv 的新手, 自行注册并测试软件!
SkyCiv S3D 设计模块
在这个部分, 我们使用 SkyCiv 中包含的板设计模块描述设计结果. 我们不解释如何建模和分析结构 (对于这些, 请参阅我们的文档中有关此主题的相关文章: 如何在 SkyCiv 中建模结构?, 如何在我的建筑模型中应用荷载? 和 如何运行线弹性分析?)
可以方便地对板应用精细网格以获得准确的设计结果. 请看下图以获得更清晰的信息.
数字 12. 更精细的网格应用于板
下一步是运行设计模块并选择计算优化钢筋面积的选项.
数字 13. 设计优化前的板混凝土属性定义.
数字 14 表示板的局部轴方向. 因为局部轴 3 是向下的, 的 “最佳” 是底部, 和 “底部” 将成为顶部, 从而正确地从设计中获取数据.
另一个重要事实是板网尺寸; 它是一个平面尺寸为 500mm x 500mm 的板状方形元件. SkyCiv S3D 将加固面积作为每个有限元的积分值给出. 从而, 如果我们想获得柱或中间条带的总钢筋面积, 我们需要计算所分析带材宽度总和的元素数量的平均值. 例如, 用于柱条, 将考虑四个要素 (4×0.5米=2米).
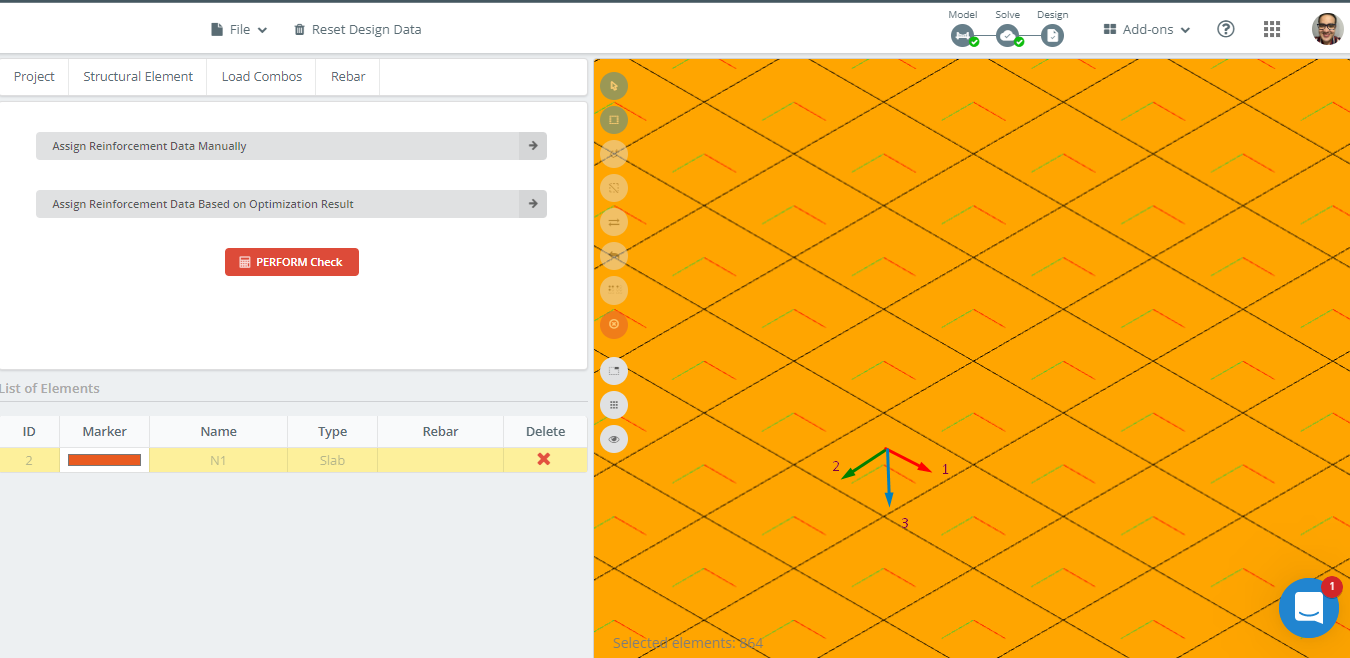
数字 14. 板示例中的局部轴方向.
第一, 我们分析沿轴纵向所需的加固面积 1.
柱条
- 外部负力矩 (顶部加固): \({一个_{s,最佳} =(119.09\次 2 + 952.72 + 833.64 )\压裂{{毫米}^ 2}{米} \乘以 0.50m = 1012.27 {毫米}^ 2}\)
- 外部积极时刻 (底部加固): \({一个_{s,机器人} = 4*463.90 \压裂{{毫米}^ 2}{米}\乘以 0.50m = 927.80 {毫米}^ 2}\)
- 外内负矩 (顶部加固): \({一个_{s,最佳} =(1071.82\次 2 +714.54 \次 2 )\压裂{{毫米}^ 2}{米} \乘以 0.50m = 1786.36 {毫米}^ 2}\)
- 内部积极时刻(底部加固): \({一个_{s,机器人} = 4*309.27 \压裂{{毫米}^ 2}{米}\乘以 0.50m = 618.54 {毫米}^ 2}\)
- 内部负矩 (顶部加固): \({一个_{s,最佳} =(714.54\次 2 +952.73 \次 2 )\压裂{{毫米}^ 2}{米} \乘以 0.50m = 1667.27 {毫米}^ 2}\)
中条
- 外部负力矩 (顶部加固): \({一个_{s,最佳} =(119.09\次 4)\压裂{{毫米}^ 2}{米} \乘以 0.50m = 238.18 {毫米}^ 2}\)
- 外部积极时刻 (底部加固): \({一个_{s,机器人} = (463.90\次 2 +412.36 \次 2 ) \压裂{{毫米}^ 2}{米}\乘以 0.50m = 876.26 {毫米}^ 2}\)
- 外内负矩 (顶部加固): \({一个_{s,最佳} =(357.27\次 2 +476.36 \次 2 )\压裂{{毫米}^ 2}{米} \乘以 0.50m = 833.63 {毫米}^ 2}\)
- 内部积极时刻(底部加固): \({一个_{s,机器人} = 4*257.72 \压裂{{毫米}^ 2}{米}\乘以 0.50m = 515.44 {毫米}^ 2}\)
- 内部负矩 (顶部加固): \({一个_{s,最佳} =(357.27\次 2 +476.36 \次 2 )\压裂{{毫米}^ 2}{米} \乘以 0.50m = 833.63 {毫米}^ 2}\)
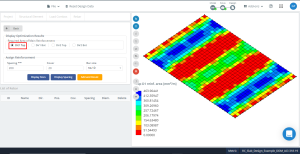
数字 15. 优化结果有方向 “1” 和顶面 (底部, 实际上).
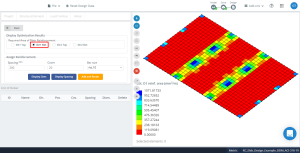
数字 16. 优化结果有方向 “1” 和底部 (顶面, 实际上).
最后, 我们分析沿轴线横向方向所需的加固面积 2.
柱条
- 外部负力矩 (顶部加固): \({一个_{s,最佳} =(91.55\次 2 + 457.73 + 549.28 )\压裂{{毫米}^ 2}{米} \乘以 0.50m = 595.055 {毫米}^ 2}\)
- 外部积极时刻 (底部加固): \({一个_{s,机器人} = (269.68\次 3+239.72) \压裂{{毫米}^ 2}{米}\乘以 0.50m = 524.38 {毫米}^ 2}\)
- 外内负矩 (顶部加固): \({一个_{s,最佳} =(823.92\次 2 +549.28 +457.73)\压裂{{毫米}^ 2}{米} \乘以 0.50m = 1327.43 {毫米}^ 2}\)
- 内部积极时刻(底部加固): \({一个_{s,机器人} = (179.79\次 3+149.82) \压裂{{毫米}^ 2}{米}\乘以 0.50m = 344.60 {毫米}^ 2}\)
- 内部负矩 (顶部加固): \({一个_{s,最佳} =(823.92\次 2 +549.28 +457.73)\压裂{{毫米}^ 2}{米} \乘以 0.50m = 1327.43 {毫米}^ 2}\)
中条
- 外部负力矩 (顶部加固): \({一个_{s,最佳} =(183.09\times 2+91.55\times 6)\压裂{{毫米}^ 2}{米} \乘以 0.50m = 457.74 {毫米}^ 2}\)
- 外部积极时刻 (底部加固): \({一个_{s,机器人} = (209.75\次 2 +179.79 \次 2 +149.82 \次 4) \压裂{{毫米}^ 2}{米}\乘以 0.50m = 689.18{毫米}^ 2}\)
- 外内负矩 (顶部加固): \({一个_{s,最佳} =(274.64\times 2+91.55\times 6)\压裂{{毫米}^ 2}{米} \乘以 0.50m = 549.29 {毫米}^ 2}\)
- 内部积极时刻(底部加固): \({一个_{s,机器人} = (119.86\次 4 + 89.89\次 4) \压裂{{毫米}^ 2}{米}\乘以 0.50m = 419.50 {毫米}^ 2}\)
- 内部负矩 (顶部加固): \({一个_{s,最佳} =(274.64\times 2+91.55\times 6 )\压裂{{毫米}^ 2}{米} \乘以 0.50m = 549.29 {毫米}^ 2}\)
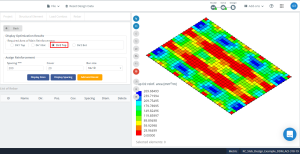
数字 17. 优化结果有方向 “2” 和顶面 (底部, 实际上).
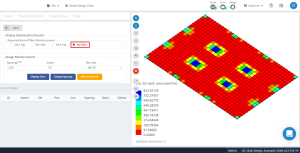
数字 18. 优化结果有方向 “2” 和底部 (顶面, 实际上).
结果比较
下表显示了 DDM 的结果 (“直接设计法”) 和 S3D 钢筋优化.
| 跨度 (ES:外部的, 是:内部的) | 柱条 (S3D设计) \({作为 ({毫米}^ 2)}\) | 柱条 (ACI-318 DDM) \({作为 ({毫米}^ 2)}\) | % 差异 | 中条 (S3D设计) \({作为 ({毫米}^ 2)}\) | 中条 (ACI-318 DDM) \({作为 ({毫米}^ 2)}\) | % 差异 |
|---|---|---|---|---|---|---|
| 外部负ES | 1012.27 | 853.996 | 15.636 | 238.18 | 0 (612.0) | 100.00 |
| 正ES | 927.80 | 1018.259 | 9.75 | 876.26 | 689.733 | 21.287 |
| 内部负ES | 1786.36 | 1740.844 | 2.48 | 833.63 | 558.322 (612.0) | 26.586 |
| 正向IS | 618.54 | 689.733 | 11.51 | 515.44 | 459.937 (612.0) | 18.734 |
| 负离子 | 1667.27 | 1609.607 | 3.459 | 833.63 | 525.642 (612.0) | 26.586 |
横向方向
| 跨度 (ES:外部的, 是:内部的) | 柱条 (S3D设计) \({作为 ({毫米}^ 2)}\) | 柱条 (ACI-318 DDM) \({作为 ({毫米}^ 2)}\) | % 差异 | 中条 (S3D设计) \({作为 ({毫米}^ 2)}\) | 中条 (ACI-318 DDM) \({作为 ({毫米}^ 2)}\) | % 差异 |
|---|---|---|---|---|---|---|
| 外部负ES | 595.055 | 518.726 | 12.827 | 457.74 | 0 (1224) | 100.00 |
| 正ES | 524.38 | 618.494 | 17.948 | 689.18 | 418.958 | 39.209 |
| 内部负ES | 1327.43 | 1057.509 | 20.334 | 549.29 | 339.247 | 38.239 |
| 正向IS | 344.60 | 418.958 | 21.578 | 419.50 | 279.42 | 33.392 |
| 负离子 | 1327.43 | 977.799 | 26.339 | 549.29 | 319.189 | 41.891 |
结论
我们在本文中演示了用于板设计的 SkyCiv 模块根据代码 ACI-318-19 计算弯板的钢筋. 比较柱条中的分析结果, 由于它们的相对刚度, 时刻高度集中, 手工计算和S3D优化之间的差异舍入为 10 – 15%. 这种实用性表明分析和设计过程之间的完美匹配.
用于中间条, 结果略有不同,因为代码仅在获取相应的列条带后分配剩余的时刻. 当我们将其与软件的分析进行比较时,这将影响比赛, 哪个更准确.
SkyCiv的新手? 注册并亲自试用该软件!

