计算挡土墙上的侧向土压力
作用在挡土墙上的主要荷载之一是侧向土压力. 是因为, 对其大小和分布进行良好估计是混凝土挡土墙设计的决定性因素. 一般来说, 根据墙体倾向于移动的方向,存在三种不同类型的侧向土压力:
- 静土压力: 当墙壁完全无法移动时
- 主动土压力: 当墙壁可能倾斜离开保留的土壤时
- 被动土压力: 当墙壁可能被推入保留的土壤时
在这篇文章中, 我们将重点描述上述每种土压力情况的公式.
侧向土压力分布
一般来说, 侧向土压力的行为与静水压力相同. 在表面处具有零值,在最深点处具有最大值,遵循两个提到的边界之间的线性分布. 因此, 水平地下应力分布由以下表达式描述:
\(\sigma_h = K_* \cdot (\伽马z)\)
在哪里 \(K_*\) 取值为 \(K_o\) 对于静止压力的情况, \(K_a\) 对于主动压力的情况, 和 \(K_p\) 对于被动压力的情况.
将给定的横向地下应力表达式从 \(0\) 至 \(H\) 在 \(z), 结果是:
\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)
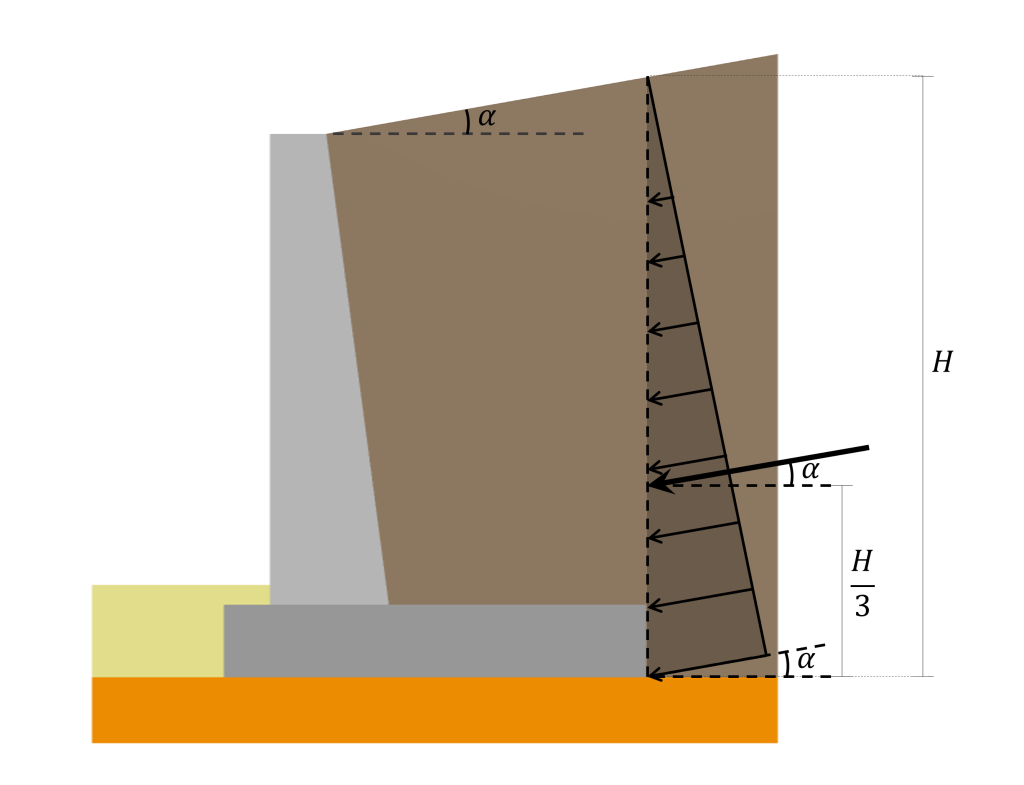
这个结果的行动路线位于 \(\压裂{2}{3}H\) 从表面上看. 侧向土压力分布, 它的结果, 和上面描述的位置如下图所示:
值得一提的是,所提出的分布和结果计算方法仅适用于作用在垂直背面的土壤压力. 对于带有倾斜背面的挡土墙 (就像上图中的那个), 土壤压力作用的表面仍被认为是垂直的,因为假定它作用在位于脚跟末端的垂直平面内.
另外, 当回填物倾斜某个角度时 \(\alpha\) 相对于水平, 压力分布及其结果以相同的角度倾斜 \(\alpha\) 如下图所示:
正确估计侧向土压力分布及其结果是挡土墙设计过程中的关键步骤. 有关如何将这种横向土压力包含在挡土墙设计过程中的更多信息, 参考文章 这里. 现在让我们深入研究计算不同条件下土壤对挡土墙施加的合成侧向土压力的公式.
静止侧向土压力
这种计算挡土墙侧向土压力的方法只能在墙完全静止并且不允许远离土壤或进入土壤的情况下使用, 这种条件确保土壤中的水平应变为零. 压力分布倾斜一个等于回填倾角的角度, 静压系数 (\(K_o\)) 是取代 \(K_*\) 在前面的方程中. 该系数是计算压力分布及其结果的唯一未知数. 对于正常固结土, 的关系 \(K_o\) 是:
\(K_o = 1-sin(\菲')\)
在哪里 \(\φ') 是考虑的土壤的有效摩擦角.
对于超固结土, 系数可以使用以下表达式计算:
\(K_o = (1-没有(\菲'))\cdot OCR^{没有(\菲')}\)
在哪里 \(\φ') 是有效摩擦角, 和 \(OCR\) 考虑的土壤超固结率.
将该系数代入计算静态侧向土压力合力的表达式中,得到:
\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)
主动侧向土压力
当墙完全不屈服时,可以使用前面的方法, 然而, 如果墙壁倾向于远离土壤, 任何深度的墙壁上的土压力都会减小. 压力分布倾斜一个等于回填倾角的角度, 主动压力系数 (\(K_a\)) 是取代 \(K_*\) 在初始方程中. 使用 Rankine 的方法 粒状回填, 并假设压力作用在 垂直背面, 主动土压力系数可用下式计算:
\(K_a=cos(\α) \压裂{cos(\α) – \sqrt{因^2(\α) – 因^2(\菲')}}{cos(\α) + \sqrt{因^2(\α) – 因^2(\菲')}}\)
在哪里 \(\φ') 是考虑的土壤的摩擦角和 \(\alpha\) 是回填面相对于水平面的倾角.
将该系数代入计算活动条件下侧向土压力合力的表达式中,得到:
\(P_a=\frac{1}{2} \gamma \cdot H^2 \cdot K_a\)
前面介绍的兰金主动压力计算是基于壁无摩擦的假设.
被动侧向土压力
当挡土墙被推入土体时,作用在挡土墙上的侧向土压力被认为是被动的, 在那种情况下, 水平应力将相对于静止状态增加. 压力分布倾斜一个等于回填倾角的角度, 被动压力系数 (\(K_p\)) 是取代 \(K_*\) 在初始方程中. 使用 Rankine 的方法 粒状回填, 并假设压力作用在 垂直背面, 被动土压力系数可以使用表达式计算:
当回填完全水平时
\(K_p = tan^2(45º+\frac{\菲'}{2})\)
当回填土相对于水平面倾斜一定角度时
\(K_p=cos(\α) \压裂{cos(\α) + \sqrt{因^2(\α) – 因^2(\菲')}}{cos(\α) – \sqrt{因^2(\α) – 因^2(\菲')}}\)
在哪里 \(\φ') 是考虑的土壤的摩擦角和 \(\alpha\) 是回填面相对于水平面的倾角.
将该系数代入计算被动条件下侧向土压力合力的表达式中,得到:
\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)
再次, 前面介绍的 Rankine 主动压力计算是基于壁无摩擦的假设.
参考资料
挡土墙计算器
SkyCiv 提供了一个免费的挡土墙计算器,可以计算墙上的横向土压力, 并对挡土墙进行稳定性分析. 付费版本还显示完整的计算, 所以你可以一步一步看到, 如何计算挡土墙抗倾覆的稳定性, 滑行, 和轴承!
产品开发人员
ng (民用)
领英