NBCC的一个完整的例子 2015 雪荷载计算
结构上积雪会严重危害屋顶构件或其他裸露的结构元素. 的 加拿大国家建筑法规 (2015) B区 – 部分 4.1.6 提供雪荷载和相关雨荷载的详细计算. 使用本指南, 我们将使用结构3D示例演示如何计算雪荷载 (S3D) 仓库模型, 如下所示:
数字 1: S3D仓库模型示例
数字 2: 使用Google地图的示例网站位置 (仅用于说明).
桌子 1: 计算雪荷载所需的建筑数据.
| 位置 | 奥格登, 卡尔加里, 艾伯塔省 (仅用于说明) |
| 占用 | 物料的仓库或储存 |
| 方面 | 19.508 x 31.70 每个结构的m 较小建筑物的屋檐高度 9.144 米 较小建筑物的顶点高度 11.941 米 上下屋顶的区别是 3.50 米 车顶俯仰角 16° |
| 额外细节 | 屋顶表面湿滑 结构之间的差距是 2.30 米 |
从表 1, 指定的雪荷载, \(S), 可以使用公式计算:
\(S = {一世}_{s}[{小号}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{一个} +{小号}_{[R}]\) (1)
在哪里:
\({一世}_{s}\) =积雪的重要因素, 表4.1.6.2-A
\({小号}_{s}\) = 1-50年地面雪荷载, 千帕, 小节 1.1.3
\({C}_{b}\) =基本屋顶雪荷载系数, 4.1.6.2 (2)
\({C}_{w}\) =基于风暴露因子, 4.1.6.2 (3) 和 (4)
\({C}_{s}\) =斜率系数, 4.1.6.2 (5), (6), 和 (7)
\({C}_{一个}\) =累积因子, 4.1.6.2 (8)
\({小号}_{[R}\) = 50年中1年相关的雨量, 千帕, 小节 1.1.3, 但不大于 \({小号}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{一个}\)
以下各节将分别检查每个参数. 将计算以下雪荷载情况: 每个屋顶上的雪量平衡和不平衡 (正常风向脊), 以及考虑到滑动积累而在下层屋顶上产生的漂移.
重要性因子, \({一世}_{s}\)
确定的第一件事是重要因素, \({一世}_{s}\), 被发现使用 表4.1.6.2-A 如所引用. 由于该结构是一栋存储建筑物,一旦发生故障,它对人类生活的直接影响很小, 重要性类别是 低的. 此外, 计算将处于极限状态 (超低硫). 所以从 表4.1.6.2-A, \({一世}_{s}\) 等于 0.80.
| 重要性类别 | 重要性因子, \({一世}_{s}\) | |
|---|---|---|
| 超低硫 | SLS | |
| 低的 | 0.8 | 0.9 |
| 普通的 | 1.0 | 0.9 |
| 高的 | 1.15 | 0.9 |
| 灾后 | 1.25 | 0.9 |
地面积雪, \({小号}_{s}\), 和相关的雨量, \(({小号}_{[R})\)
地面积雪, \({小号}_{s}\), 和相关的雨量, \(({小号}_{[R})\), 值列在 附录C, NBCC B部 2015 取决于位置和省. 对于这个例子, 相应的 \({小号}_{s}\) 和 \(({小号}_{[R})\) 在 卡尔加里艾伯塔省 等于 1.10 千帕 和 0.1 千帕, 分别.
难以搜寻NBCC的地面积雪和相关的雨量 2015? 尝试 的 SkyCiv免费负载生成器工具 加快搜索速度并获得相应的 \({小号}_{s}\) 和 \({小号}_{[R}\) 根据您的结构的位置.
风暴露因子, \({C}_{w}\)
对于风的暴露因子, \({C}_{w}\), 它应被允许等于 1.0 基于 4.1.6.2 (3). 只要在 4.1.6.2 (4) 很满意. 对于这个例子, \({C}_{w}\) 等于 1.0 因为该位置不是一个使结构完全暴露在风中的开放地形.
基本屋顶积雪系数, \({C}_{b}\)
屋顶基本雪荷载系数, \({C}_{b}\), 可以使用以下公式计算, 如参考 4.1.6.2 (2):
\({C}_{b} = 0.8\) (2) 对于 \({升}_{C} ≤ (70/{{C}_{w}}^{2})\) 和
\({C}_{b} = (1/{C}_{w}) [1 – (1 – 0.8{C}_{w})经验值(-0.01({升}_{C}{{C}_{w}}^{2} – 70))] \) (3) 对于 \({升}_{C} > (70/{{C}_{w}}^{2})\)
在哪里:
\({升}_{C}\) =上层或下层屋顶的特征长度定义为: \(2w -{w}^{2}/l\)
\(l\) =屋顶的较大平面尺寸
\(w\) =较小的屋顶平面尺寸
对于这个例子,\(l\) 和 \(w\) 等于 31.7 m和 19.51 米, 分别, 因此, \({升}_{C}\) 等于 27.01. 以来 \({升}_{C}\) 小于 \((70/{1.0}^{2})\), 基本屋顶积雪系数, \({C}_{b}\), 等于 0.8.
斜率系数, \({C}_{s}\)
斜率因子的计算为 \({C}_{s}\) 详细介绍 4.1.6.2 (5), (6), 和 (7) 如下所示.
畅通无阻的光滑屋顶:
\({C}_{s} = 1.0\) 对于 \(α ≤ 15°\)
\({C}_{s} = 0\) 对于 \(一种 > 60°\)
\({C}_{s} = (60° – 一种)/45°\) 对于 \(15° < α ≤ 60°\)
对于其他情况:
\({C}_{s} = 1.0\) 对于 \(α ≤ 30°\)
\({C}_{s} = 0\) 对于 \(一种 > 70°\)
\({C}_{s} = (70° – 一种)/40°\) 对于 \(30° < α ≤ 70°\)
雪比重, \(γ\)
雪的具体重量在 4.1.6.13 并应视为:
\(γ= 0.43{小号}_{s} + 2.2 千牛/{米}^{3} ≤4.0kN /{米}^{3}\) (4)
对于这个例子, \(γ\) 等于 \(2.673 千牛/{米}^{3}\).
积累因子, \({C}_{一个}\)
积累因子, \({C}_{一个}\), 升 升 4.1.6.2 (8). 升.
规定的雪荷载, \(S)
在这个部分, 规定的雪荷载, \(S), 将针对平衡和漂移的情况进行计算.
平衡/不漂流的情况
对于平衡/未浸透的情况, 的 积累因子 \({C}_{一个}\) 等于 1.0. 此外, 升 \(α\) 是 \(16°\) 并且假定屋顶表面畅通无阻, 斜率因子, \({C}_{s}\), 在我们的例子中等于 0.978. 使用方程式 (1), 指定的雪荷载, \(S), 对于平衡/未过滤的情况是:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 千帕
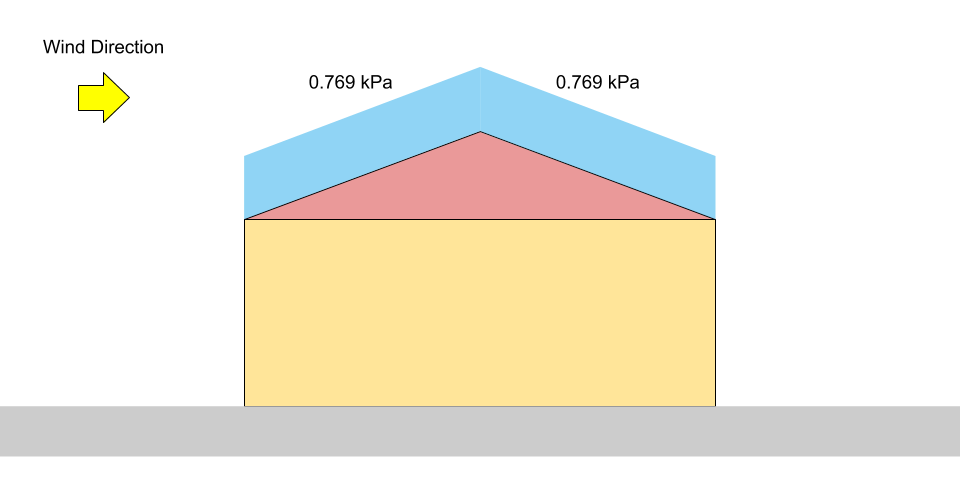
数字 3: 山墙屋顶平衡雪荷载的荷载图.
不平衡/漏水的情况
风向法线对脊
由于结构具有山墙屋顶, 不平衡的雪荷载 (垂直于山脊的风) 积累因子 \({C}_{一个}\) 被发现使用 4.1.6.9:
\({C}_{一个, 迎风} = 0\)
\({C}_{一个, 顺风} = 0.25 +α/20\) 对于 \(15° ≤ α ≤ 20°\)
\({C}_{一个, 顺风} = 1.25\) 对于 \(20° < α ≤ 90°\)
因为两个结构的屋顶俯仰角均等于16°, 积累因子 \({C}_{一个, 迎风}\) 和 \({C}_{一个, 顺风}\) 等于 0 和 1.05, 分别. 此外, 升 \(α\) 是 \(16°\) 并且假定屋顶表面畅通无阻, 斜率因子, \({C}_{s}\), 在我们的例子中等于 0.978.
在不平衡/漂移的情况下垂直于山脊, \({C}_{一个}\) 应基于 4.1.6.9 用于山形屋顶案例. 从上面的计算, \({C}_{一个, 迎风} = 0\) 和 \({C}_{一个, 顺风} = 1.05\). 因此, 两侧的指定雪荷载为:
\({小号}_{迎风} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 千帕 = \({p}_{1}\)
\({小号}_{顺风} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 千帕 = \({p}_{2}\)
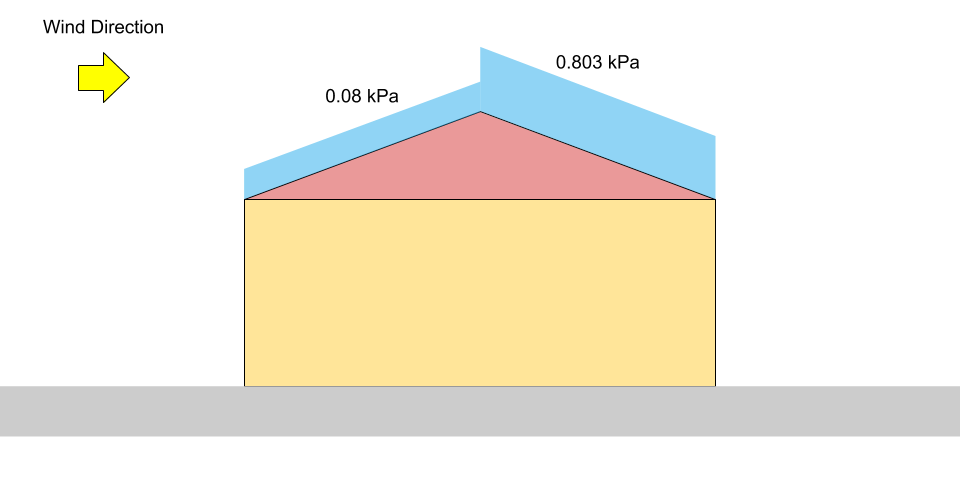
数字 4: 山墙屋顶雪荷载不平衡的荷载图 (不按比例).
风向平行于脊 – 案例一 – 风从上到下屋顶
当风平行于山脊时, 下层屋顶很可能会形成积雪. 升 积累因子 \({C}_{一个}\), 来自以下公式 4.1.6.2 (8) 被使用:
\({C}_{一个} ={C}_{00} – ({C}_{00} – 1)(X/{X}_{d})\) 对于 \(0 ≤x≤ {X}_{d}\)
\({C}_{一个} = 1.0\) 对于 \(X > {X}_{d}\)
在哪里:
\({C}_{00}\) =的峰值 \({C}_{00}\) 在x = 0
\(x\) =距屋顶台阶的距离
\({X}_{d}\) =漂移长度,如图所示 3 下面
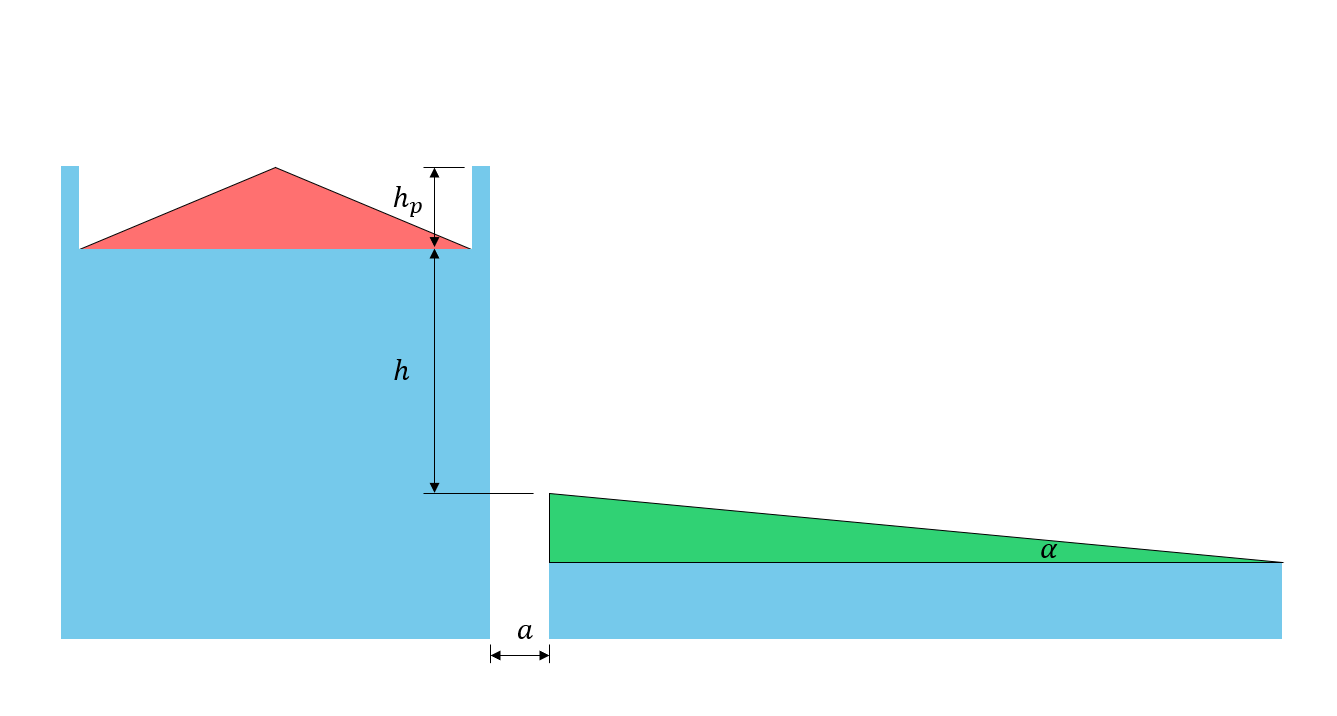
数字 5: 屋顶尺寸参数说明
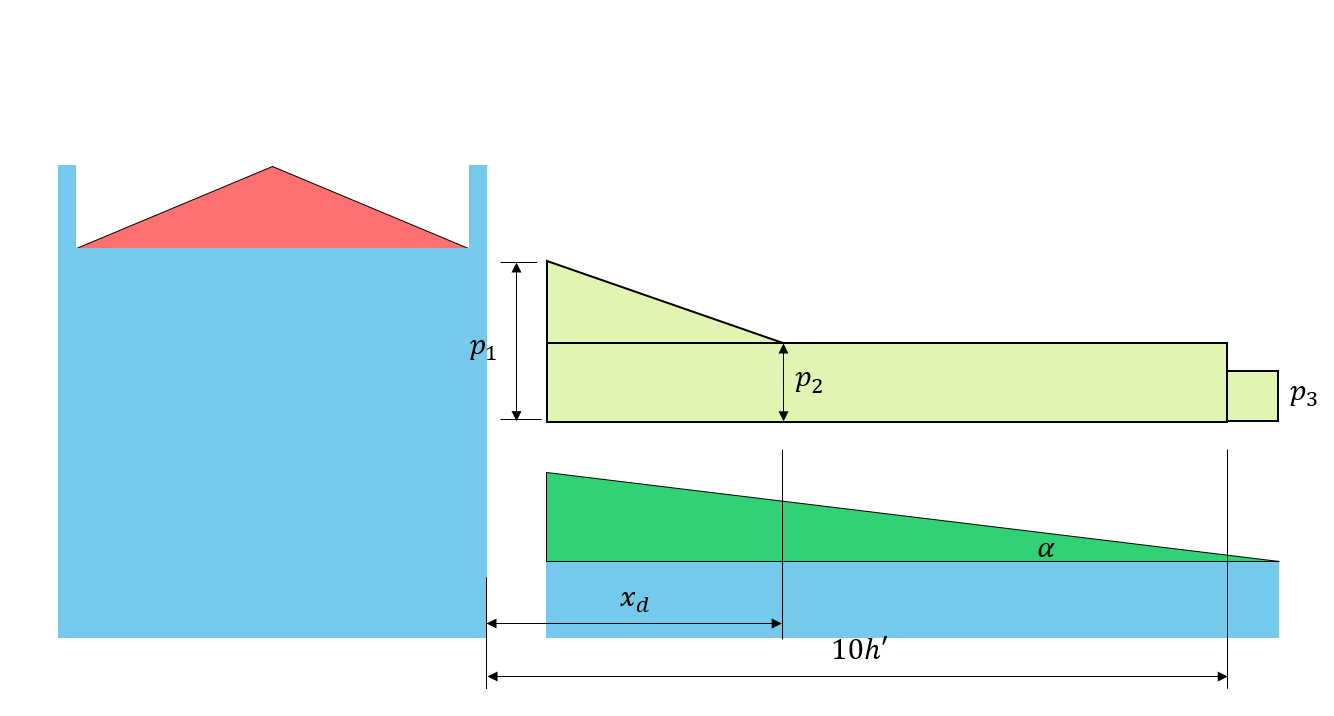
数字 6: 基于 图4.1.6.5-A.
\({C}_{00}\) 和 \({X}_{d}\) 可以使用以下公式计算:
\({C}_{00} = frac{βγh}{{C}_{b}{小号}_{s}}\) 要么 \({C}_{00} = frac{F}{{C}_{b}}\) (5), 以较小者为准
\({X}_{d} = 5 \压裂{{C}_{b}{小号}_{s}}{C}({C}_{00} – 1)\) (6)
\(F = 0.35β\sqrt{\压裂{C({升}_{cs} – 5{{H}_{p}}^{‘})}{{小号}_{s}}} +{C}_{b}\) 但 \(F≤ 5\) 对于 \({C}_{ws} = 1.0\) (7)
\({H}^{‘} =小时 – \压裂{{C}_{b}{C}_{w}{小号}_{s}}{C}\) (8)
\({{H}_{p}}^{‘} ={H}_{p} – \压裂{0.8{小号}_{s}}{C}\) 但 \(0 ≤ {{H}_{p}}^{‘} ≤ \frac{{升}_{cs}}{5}\) (9)
在哪里:
\({H}_{p}\) =上层屋顶的护墙高度 (0 在这种情况下,因为没有护栏)
\(H) =上下屋顶高度之间的高度差
\({C}_{ws}\) =的值 \({C}_{w}\) 适用于漂移源
\({升}_{cs}\) =源区域的特征长度,定义为: \(2{w}_{s} -{{w}_{s}}^{2}/{升}_{s}\)
\({升}_{s}\) =源区域的较大平面尺寸,如图所示 7 和 8, 如下图所示
\({w}_{s}\) =源区域的较小平面尺寸,如图所示 7 和 8, 如下图所示
\(β\) = 1.0 对于案例一, 和 0.67 对于案例II和III.
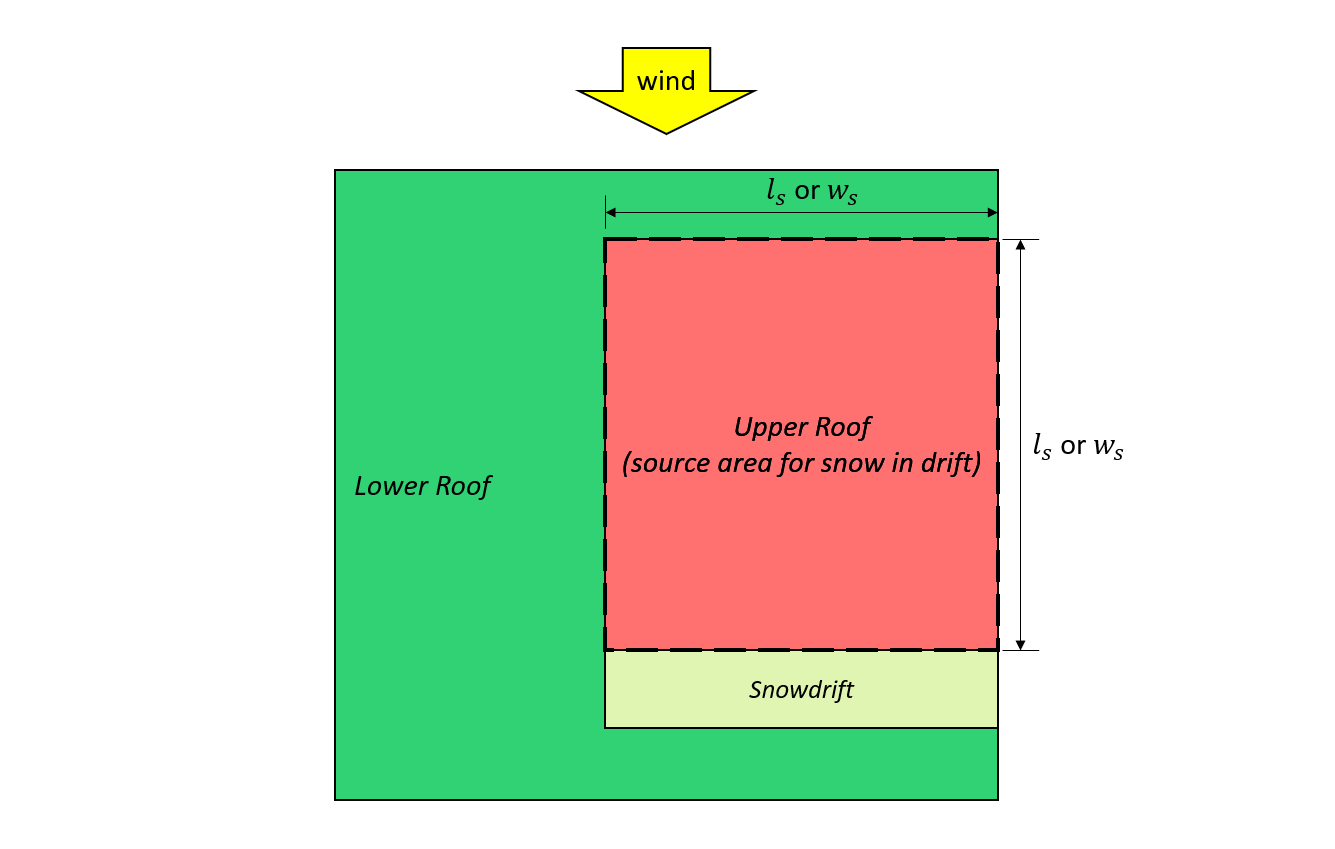
数字 7: 案例一 – 飘雪是由来自上层屋顶的风形成的 图4.1.6.5-B.
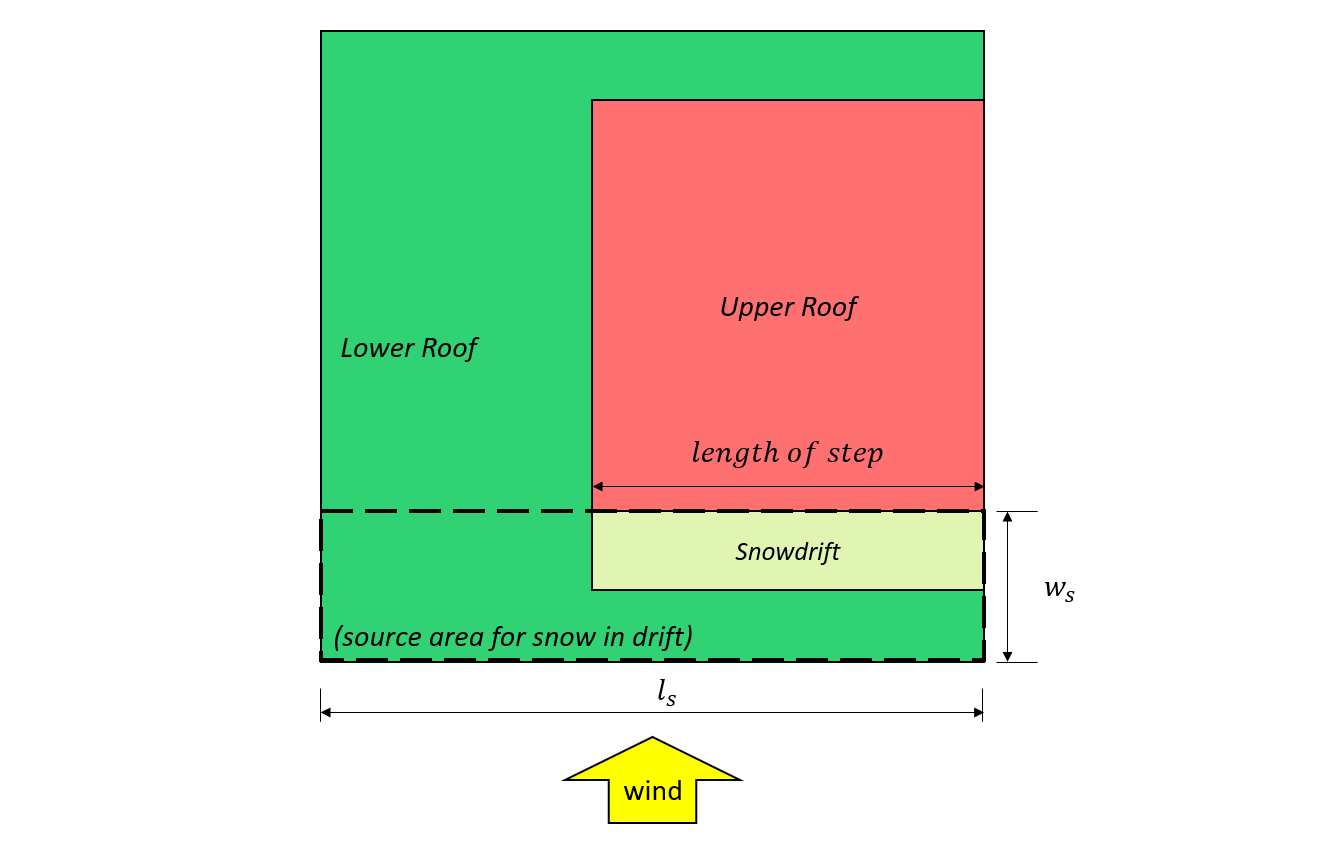
数字 8: 案例二 – 来自下层屋顶的风形成的雪堆基于 图4.1.6.5-B.
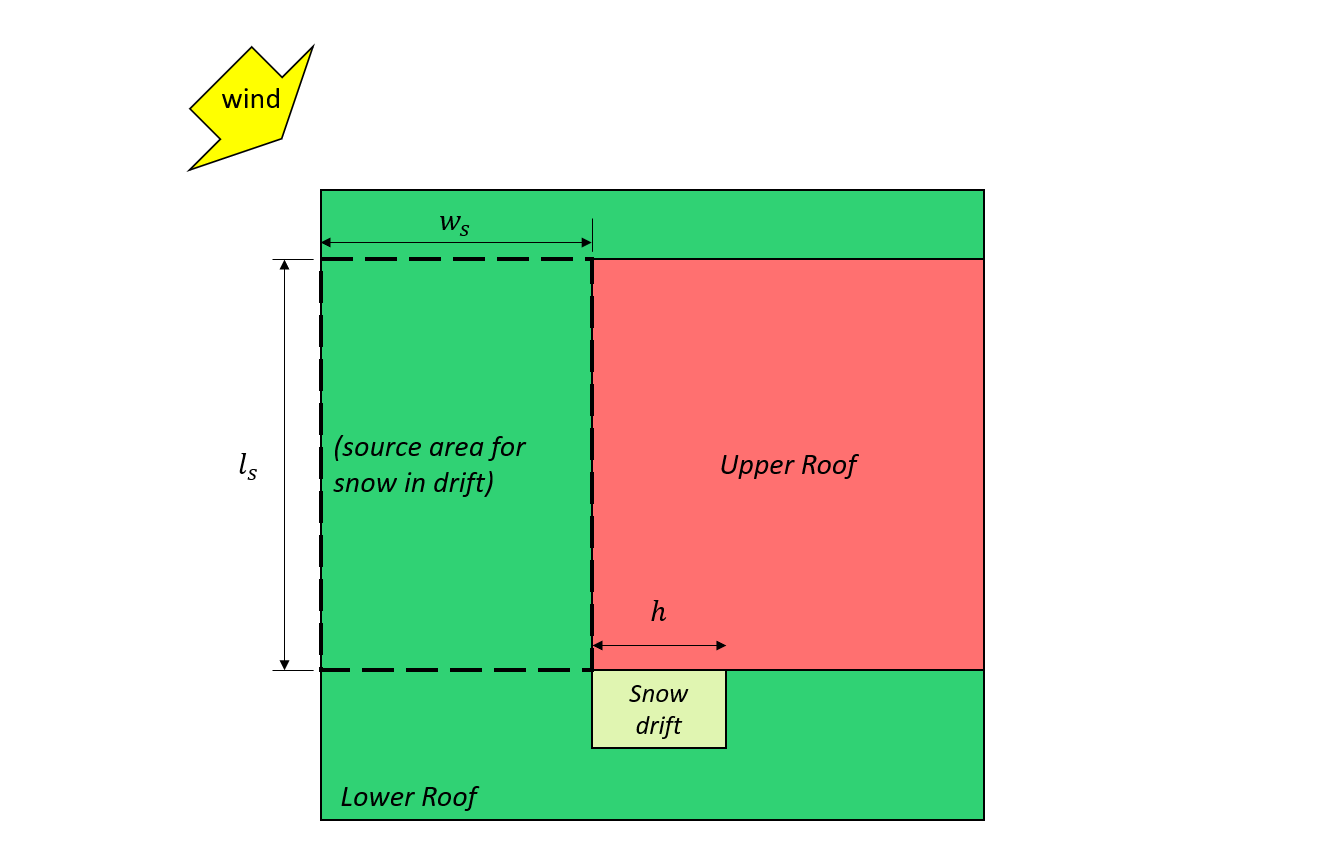
数字 7: 情况三 – 来自下层屋顶的风形成的部分雪堆基于 图4.1.6.5-B.
对于这个例子, 情况一和二将被考虑.
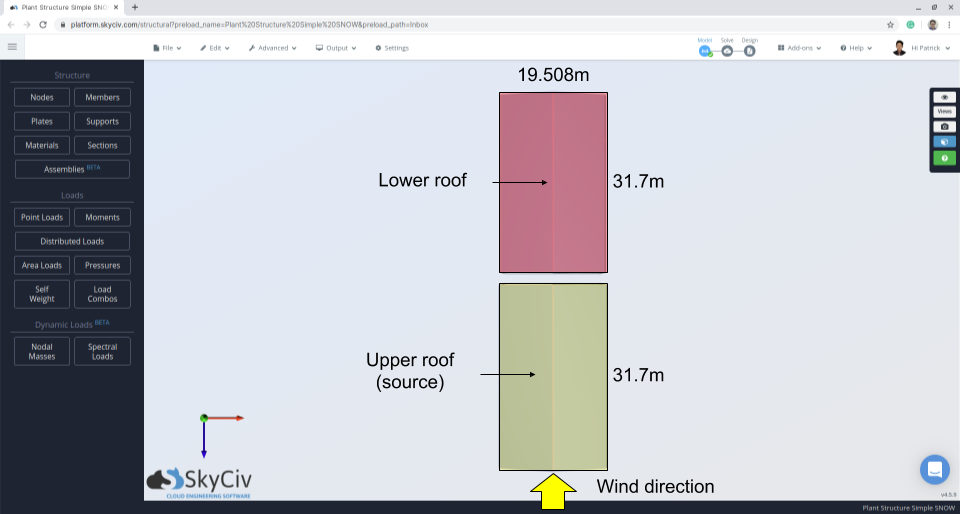
数字 10: 指示风向和风源区域的结构图.
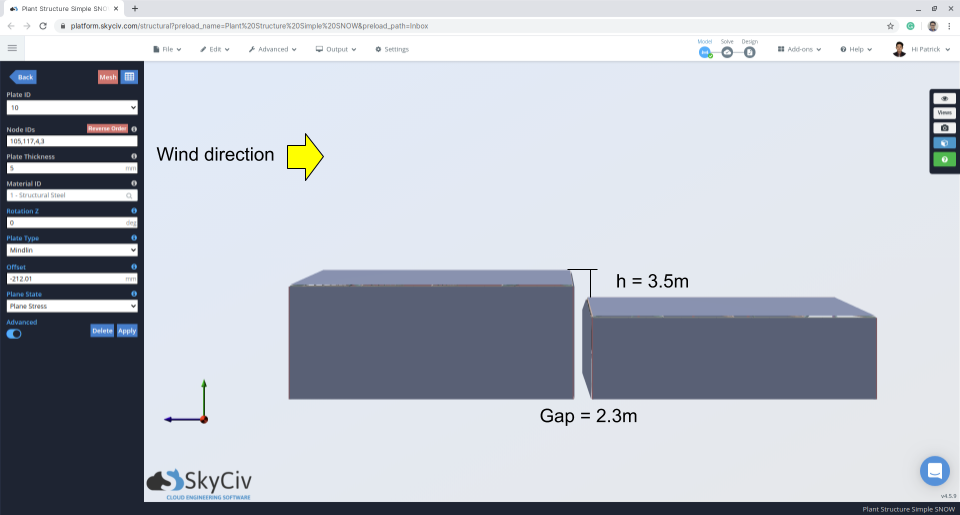
数字 11: 表示上下车顶的间隙和差异的立面图.
对于不平衡/漂移的情况,平行于山脊, \({C}_{一个}\) 应根据以下条件为案例I和案例II计算 4.1.6.5 用于多层屋顶. 对于案例一, 以下这些参数应首先使用本示例中先前提到的各种方程式进行计算:
\(β= 1.0\)
\({H}^{‘} = (3.5) – \压裂{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 米)
\({H}_{p} = 0\)
\({{H}_{p}}^{‘} =0\)
\({升}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 米)
\(F = 0.35(1.0)\sqrt{\压裂{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({C}_{00} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) 要么 \({C}_{00} = frac{3.66}{0.8} = 4.544\)
\({C}_{00} = 4.544\)
\({X}_{d} = 5 \压裂{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 米)
从这些参数, 积累因子, \({C}_{一个}\), 可以通过代入的值来计算 \({C}_{00}\) 在每一个 \(x\) 距离. 注意,我们需要计算 \({C}_{一个}\) 在 \(x = a\) 哪里 \(a\) 是屋顶之间的间隙,因为屋顶间隙小于 5 m如 4.1.6.6.
在 \(x = 0\): \({C}_{一个} = 4.544 – (4.544 – 1)(0/5.835) = 4.544\)
在 \(x = a\): \({C}_{一个} = 4.544 – (4.544 – 1)(2.3/5.835) = 3.147\)
在 \(x = {X}_{d}\): \({C}_{一个} =1.0\)
在 \(x = 10{H}^{‘}\): \({C}_{一个} =1.0\)
升 升 升, \({C}_{s} = 1.0\). 此外, 在上屋顶找到指定的雪荷载时, 积累因子, \({C}_{一个}\), 和斜率因子, \({C}_{s}\), 都等于 1.0. 因此, 每个位置的指定雪荷载的大小为:
在 \(x = 0\): \(S = 0.8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa\)
在 \(x = a\): \(S = 0.8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
在 \(x = {X}_{d}\): \(S = 0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
在上层屋顶: \(S = 0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)
风向平行于脊 – 案例二 – 风从下到上屋顶
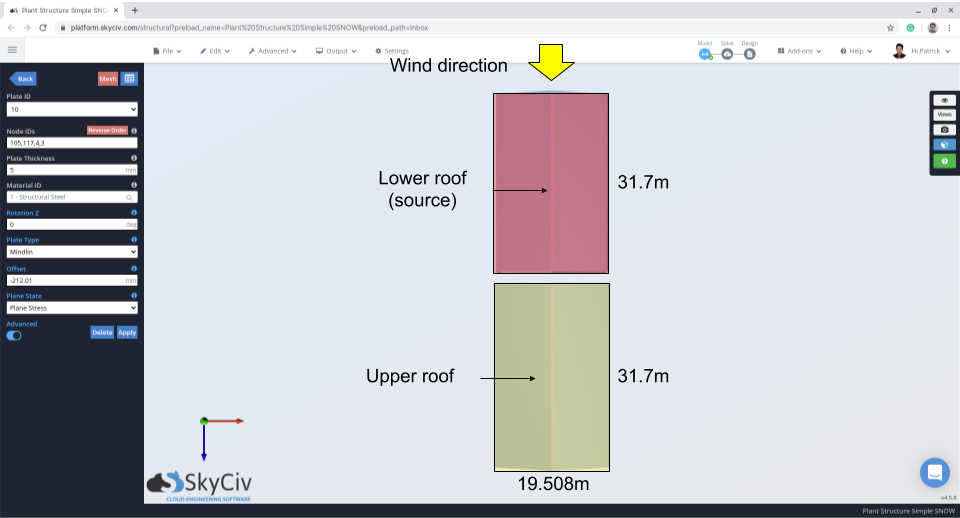
数字 12: 指示风向和风源区域的结构图 – 从下屋顶到上风.
对于案例二, 计算与案例一相似,但有不同 \(β= 0.67\):
\(β= 0.67\)
\({H}^{‘} = (3.5) – \压裂{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 米)
\({H}_{p} = 0\)
\({{H}_{p}}^{‘} =0\)
\({升}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 米)
\(F = 0.35(0.67)\sqrt{\压裂{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({C}_{00} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) 要么 \({C}_{00} = frac{2.70}{0.8} = 3.375\)
\({C}_{00} = 3.375\)
\({X}_{d} = 5 \压裂{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 米)
在 \(x = 0\): \({C}_{一个} = 3.375 – (3.375 – 1)(0/3.909) = 3.375\)
在 \(x = a\): \({C}_{一个} = 3.375 – (3.375 – 1)(2.3/3.909) = 1.978\)
在 \(x = {X}_{d}\): \({C}_{一个} =1.0\)
在 \(x = 10{H}^{‘}\): \({C}_{一个} =1.0\)
在 \(x = 0\): \(S = 0.8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa\)
在 \(x = a\): \(S = 0.8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
在 \(x = {X}_{d}\): \(S = 0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
在上层屋顶: \(S = 0.8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)
为了说明, 相应的 \({p}_{1}\), \({p}_{2}\), 和 \({p}_{3}\) 如图所示 13 和 14 下面针对案例I和案例II, 分别.
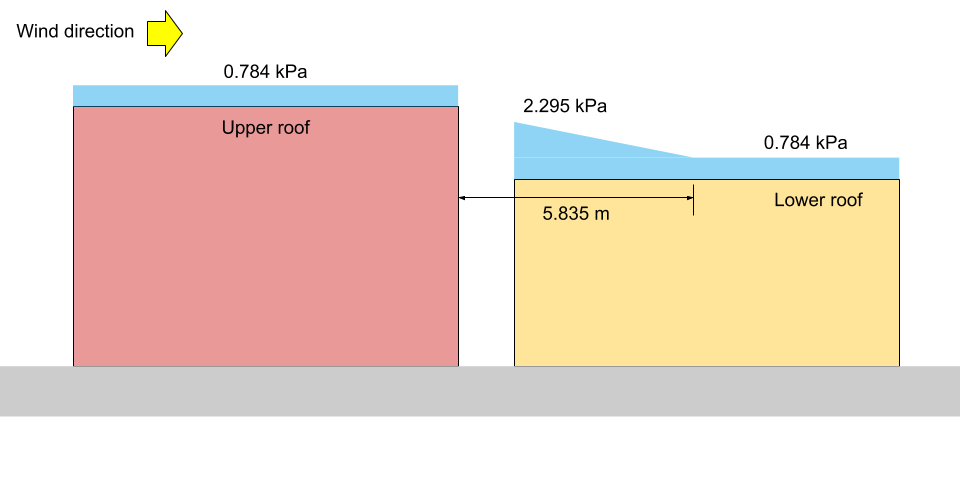
数字 13: 案例一的雪荷载图 (不按比例).
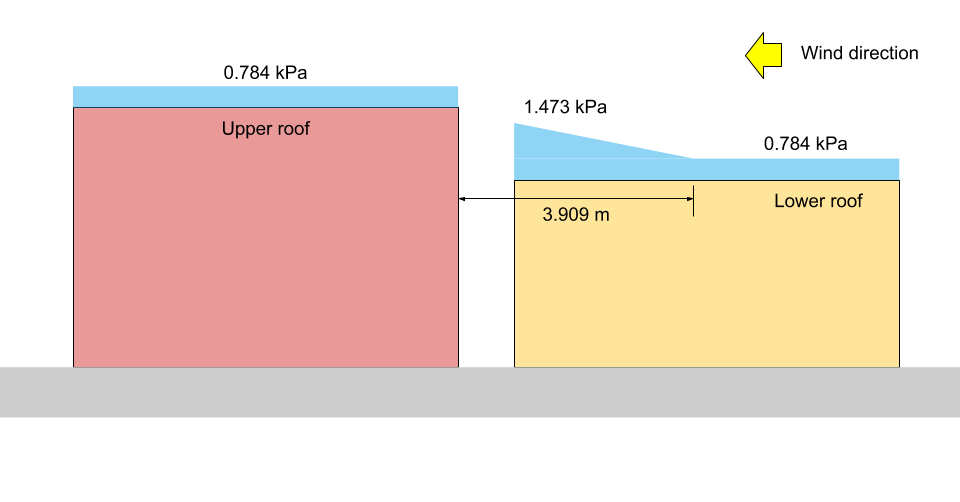
数字 14: 案例二的雪荷载图 (不按比例).
在数分钟内自动完成这些计算
那是一个很长的计算, 您作为工程师可以做什么,以加快您未来项目的流程? 最近,SkyCiv已发布并自动将Snow Load Generator作为SkyCiv Load Generator的一部分, 也会产生风荷载. 查找所示示例的雪荷载, 使用该工具只需点击几下:
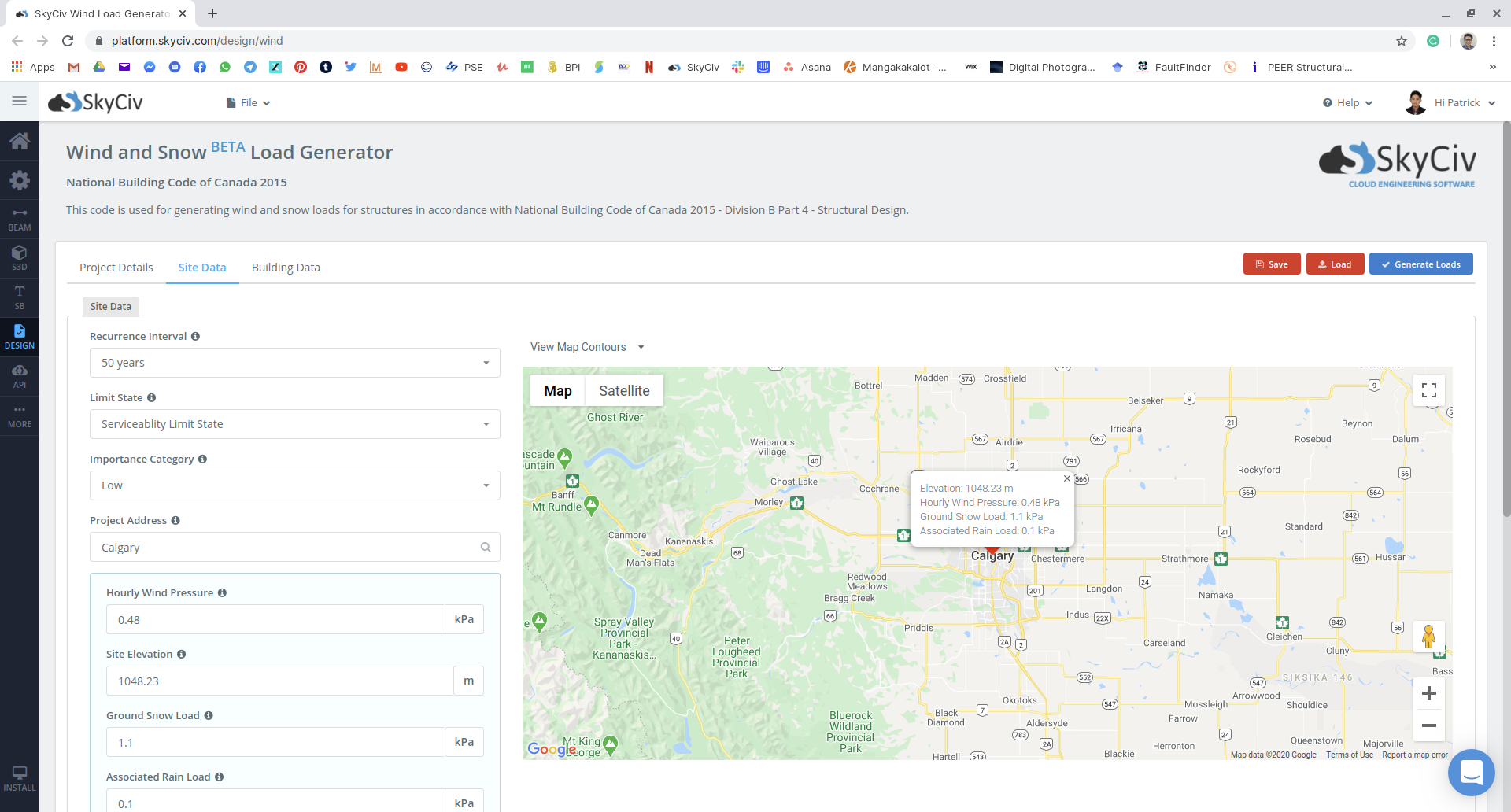
数字 15: 使用我们的示例在SkyCiv Load Generator模块上输入站点数据.
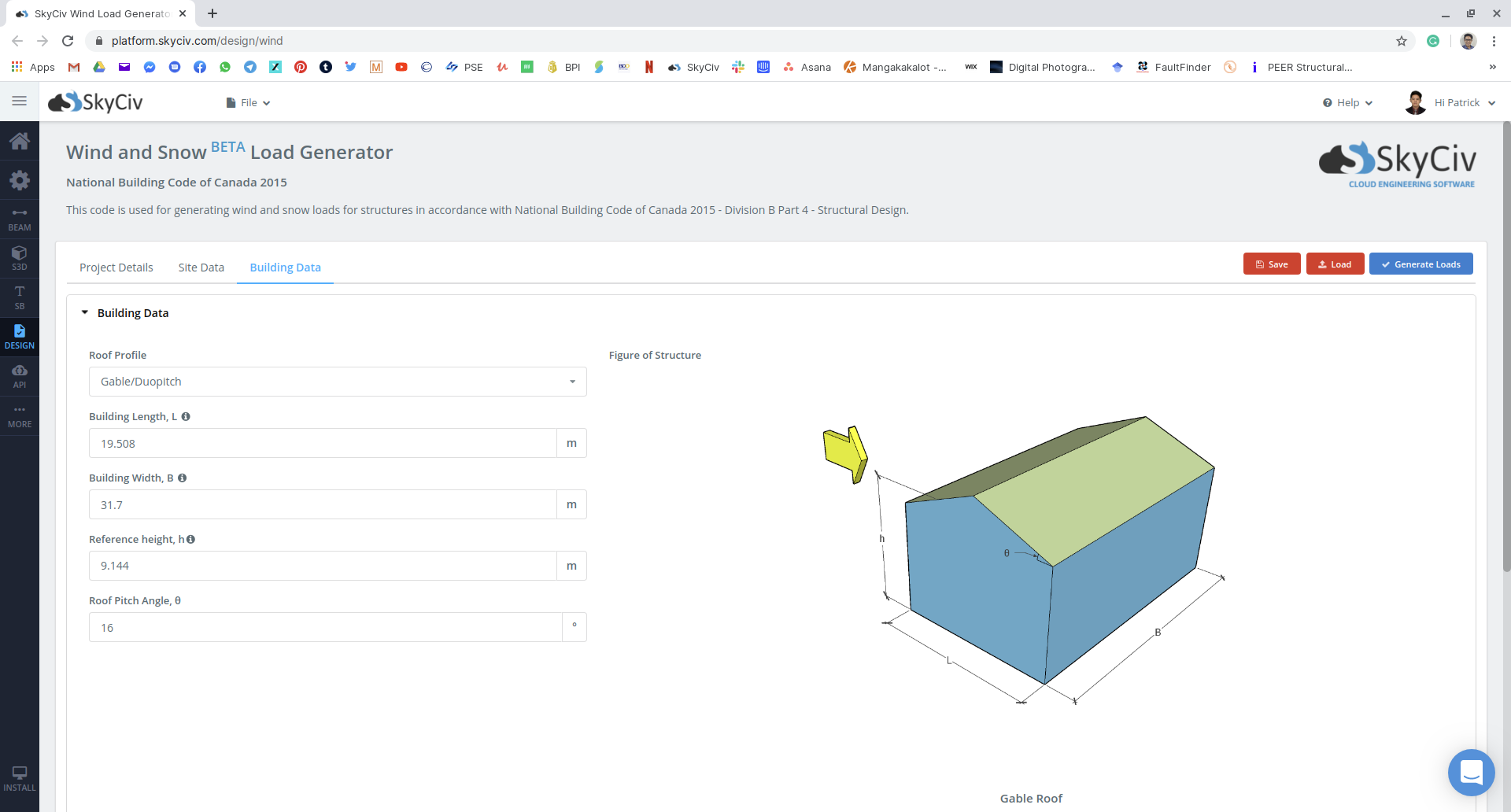
数字 16: 使用我们的示例在SkyCiv Load Generator模块上输入建筑和降雪参数.
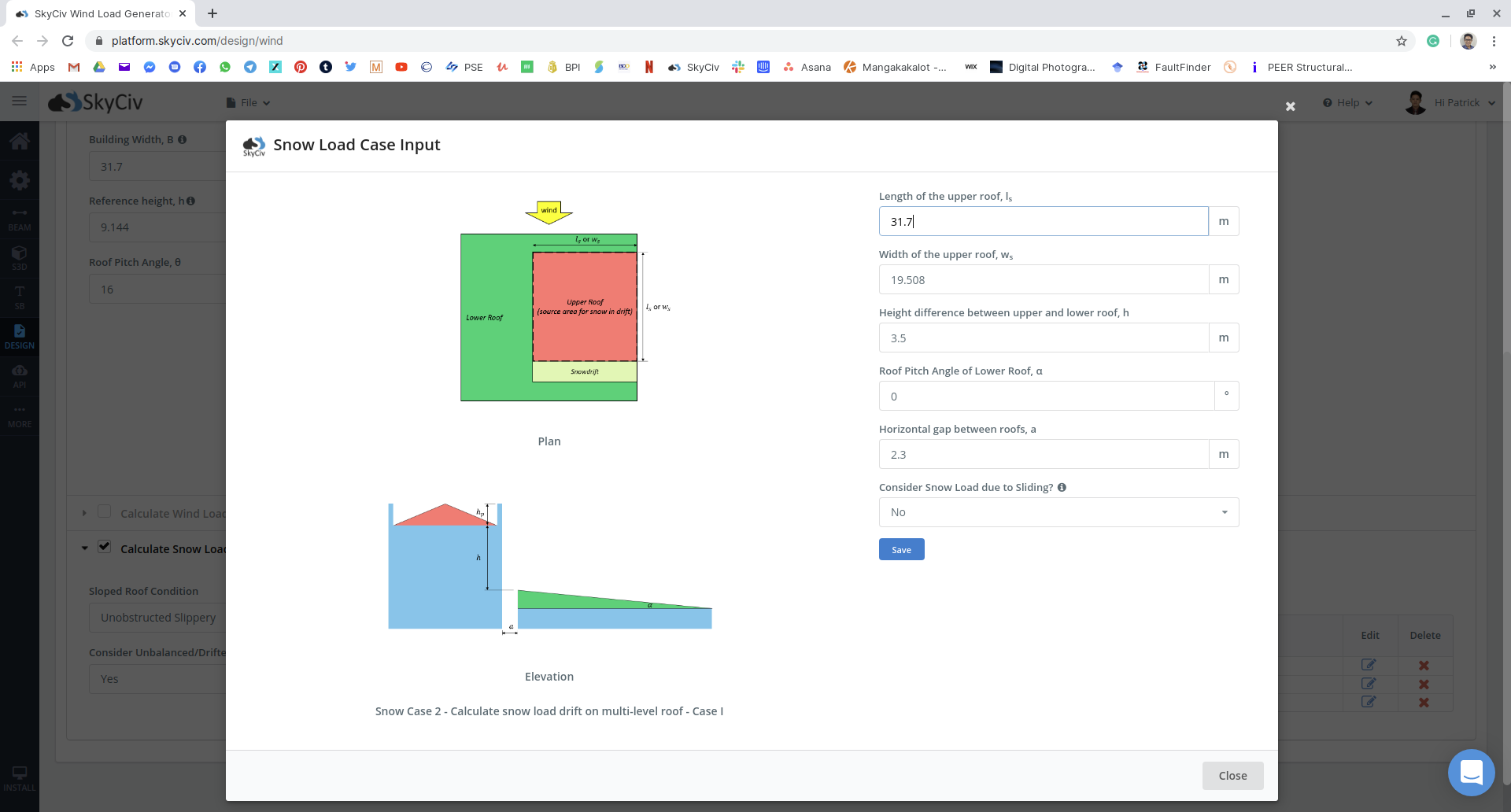
数字 17: 示例中的多个不平衡情况下的雪荷载输入.
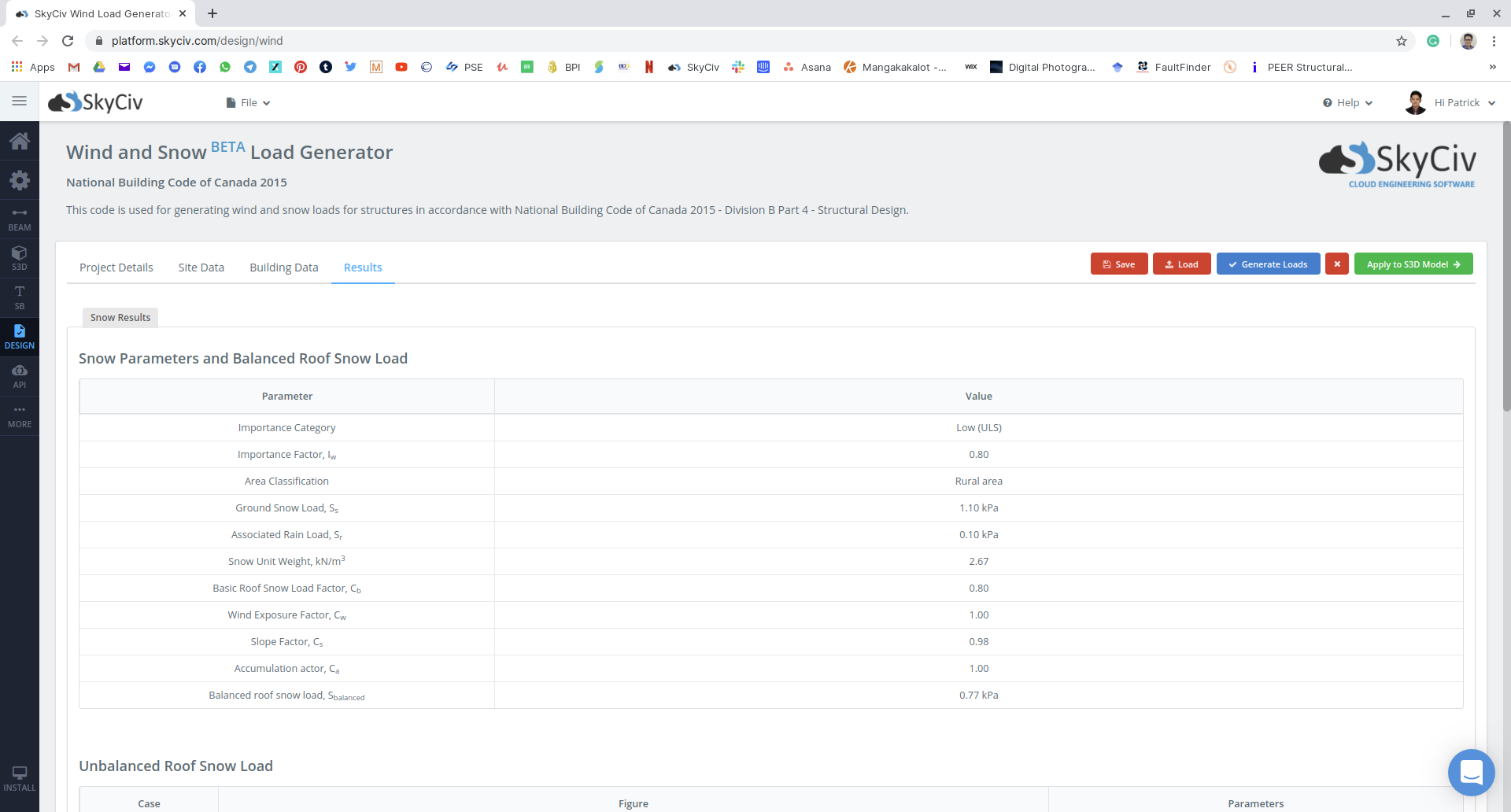
数字 18: 使用的雪荷载参数汇总以及将应用于结构的平衡雪荷载.
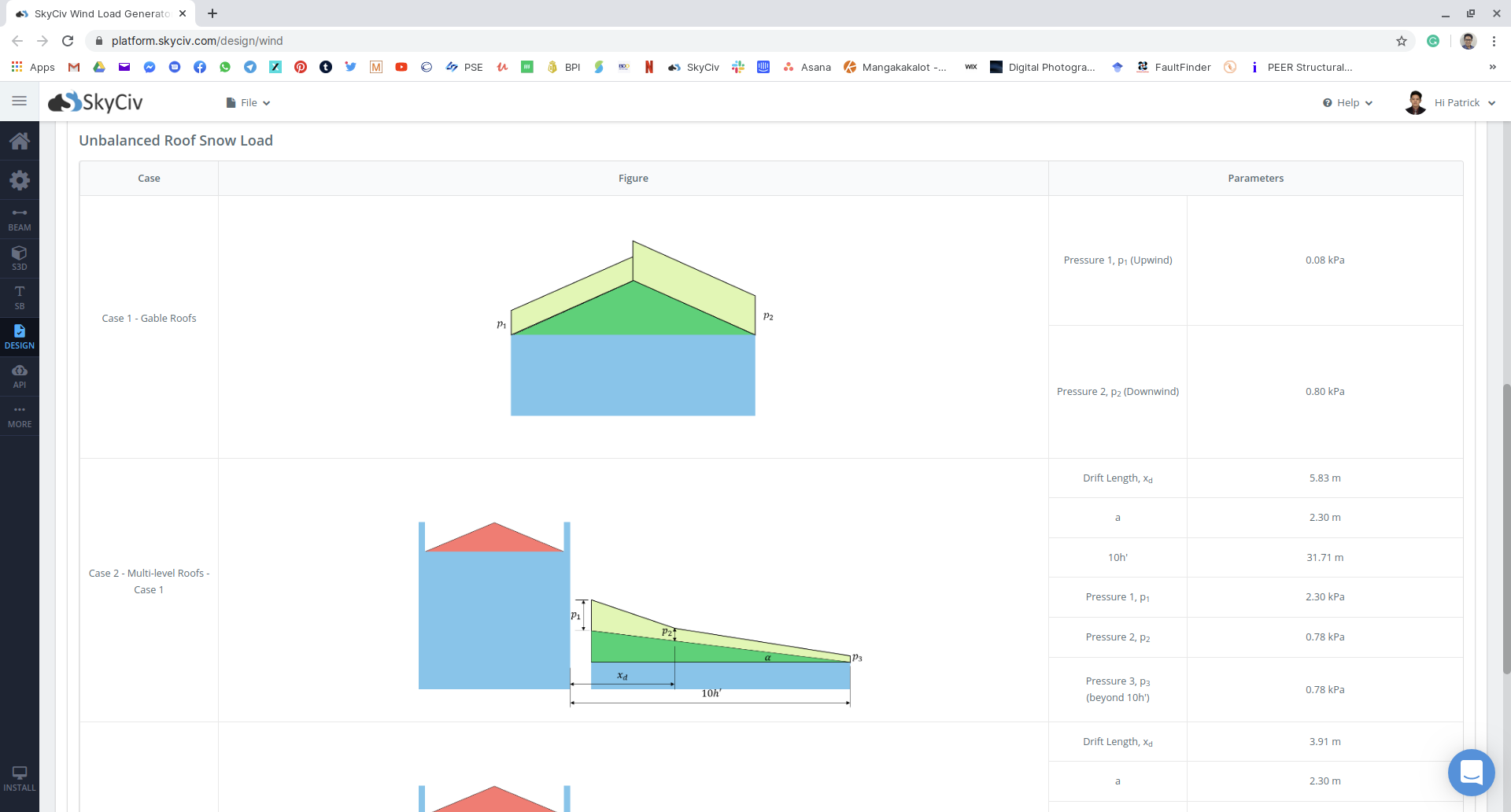
数字 19: 积雪不平衡结果汇总.
参考代码(例如ASCE)支持SkyCiv Load Generator模块中的雪荷载计算 7-10, 7-16, 在 1991-1-3, NBCC 2015, 和AS / NZS 1170.3, 并且可以在 单机版 (仅负载生成器) 和 专业的 帐目. 熟悉编程和API? 此功能可以通过使用 SkyCiv API.
结构工程师, 产品开发
土木工程硕士
领英
参考资料:
- 加拿大国家研究委员会. (2015). 加拿大国家建筑法规, 2015. 加拿大国家研究委员会.
注意:
- NBCC代码参考 “基本屋顶积雪系数” — 寻找 4.1.6.2 句子 (2)
- NBCC代码参考 “风暴露因子” — 寻找 4.1.6.2 句子 (3) 和 (4)
- NBCC代码参考 “斜率系数” — 寻找 4.1.6.2 句子 (5), (6), 和 (7)
- NBCC代码参考 “积累因子” — 寻找 4.1.6.2 句子 (8), 4.1.6.5 用于多层屋顶, 4.1.6.6 用于带缝隙的屋顶, 和 4.1.6.9 用于山墙屋顶


