SkyCiv Load Generator 最近添加了符合 ASCE7-16 的地震荷载计算. 这涉及整合 USGS 地震数据并对其进行处理以使用剖面生成地震基础剪切 12.8 等效横向程序. 在这篇文章中, 我们将深入研究使用 ASCE 计算建筑物地震荷载的过程 7-16.
SkyCiv 现在集成了来自 USGS Web API 的现场地震数据. 试试我们的 SkyCiv负载生成器!
结构数据
在这个例子中, 我们将使用以下数据计算地震荷载:
桌子 1. 我们的地震荷载计算所需的建筑数据.
| 位置 | 8050 西南比弗顿希尔斯代尔高速公路, 波特兰, 要么 97225, 美国 |
| 占用 | 住宅楼 |
| 方面 | 64 英尺 (4 海湾) × 104 英尺 (6 海湾) 计划中 楼层高度 15 英尺 电梯屋顶高度. 75 英尺 屋顶平台 柱: 20″x20″ 光束: 14″x20″ 大板: 8″ 厚度 |
| 载入中 | 混凝土单位重量 : 156 pcf 叠加恒载 (在地上): 100 psf 叠加恒载 (在屋顶上): 50 psf |
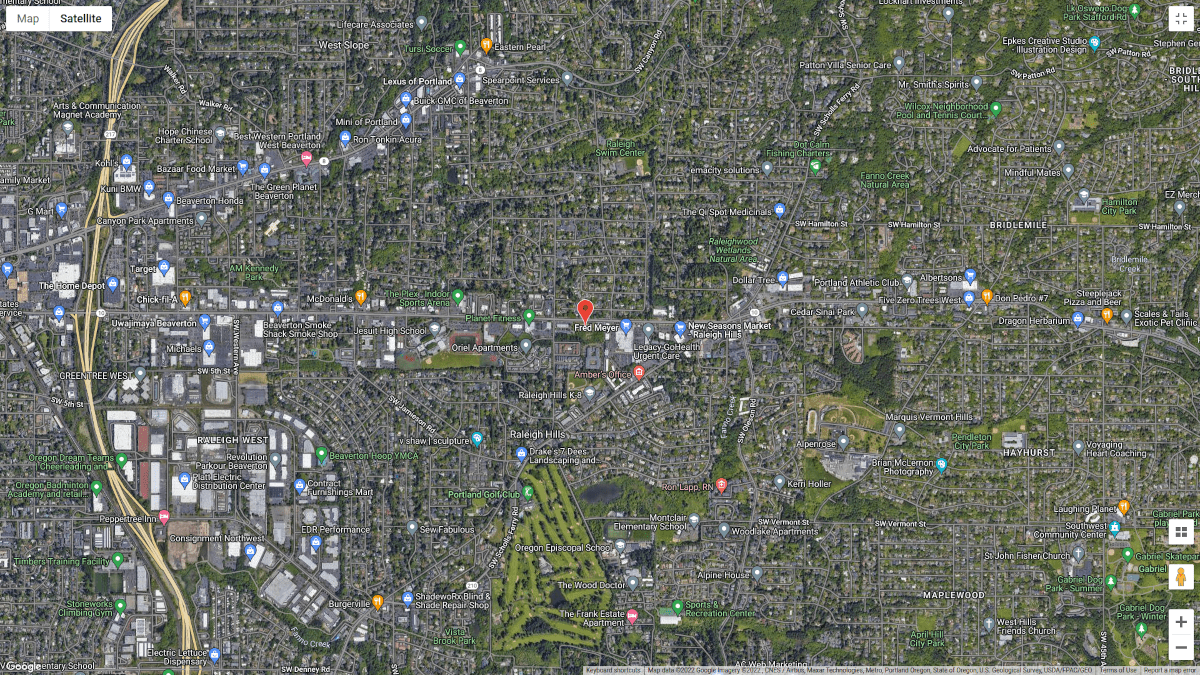
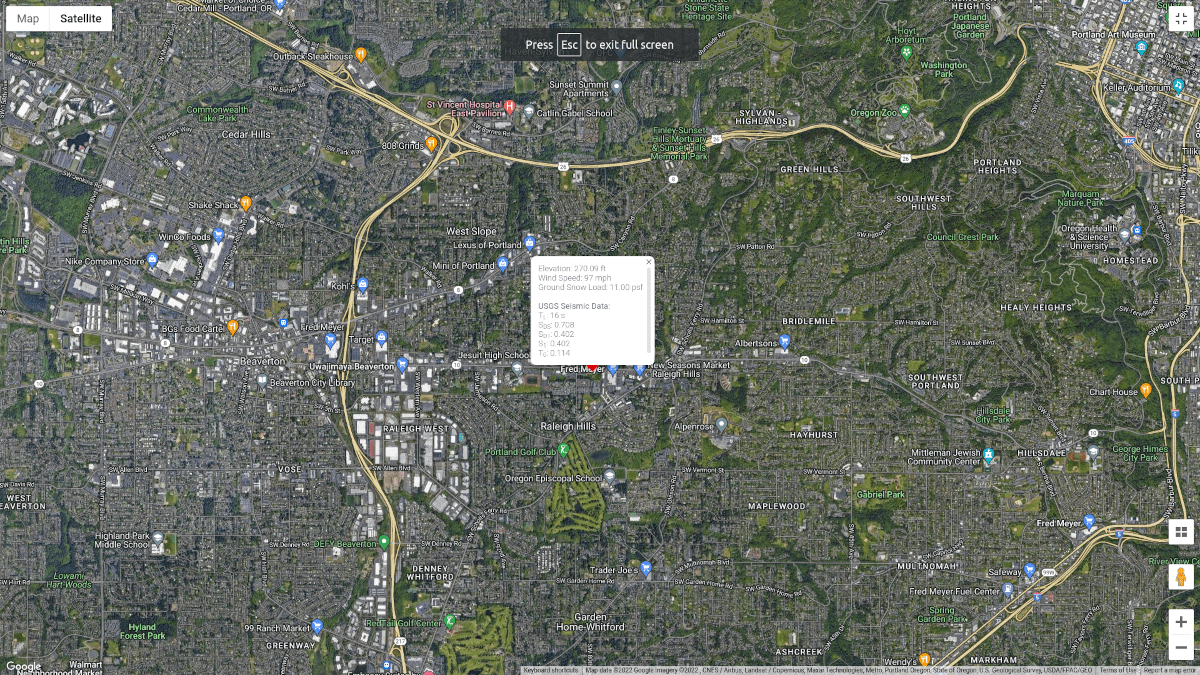
数字 1. 地点坐标 (从Google地图).
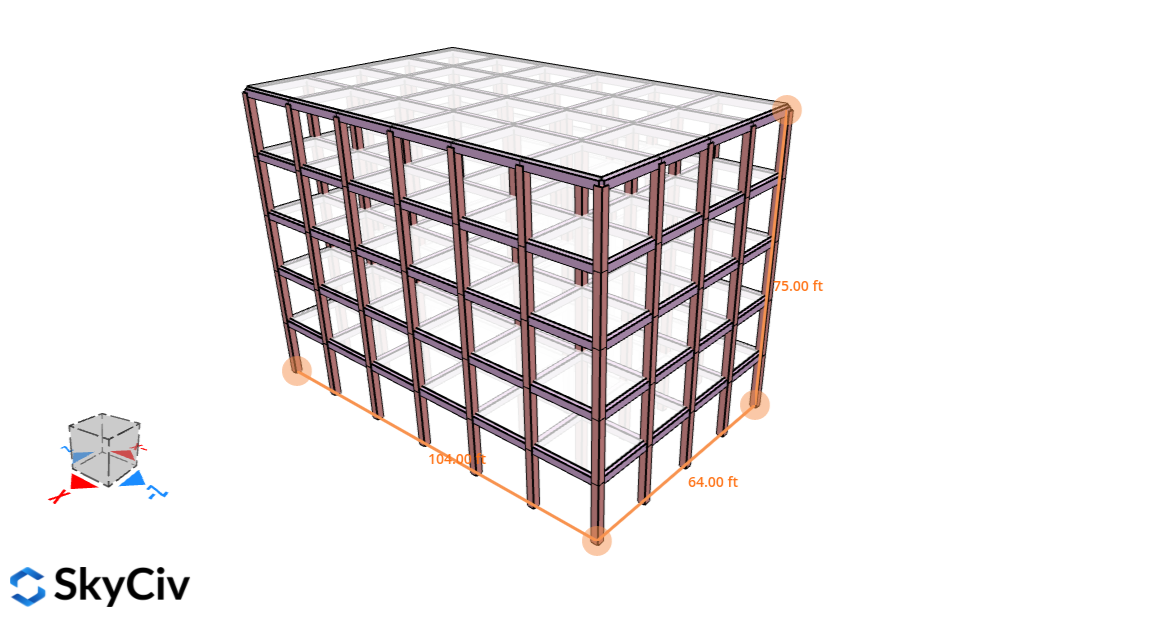
数字 2. 此示例的结构.
美国地质勘探局地震数据
美国地质勘探局有一个 开源现场地震数据 可以从他们的 Design Web Services API 中使用. 在这个计算中, 我们只需要以下数据:
- \({小号}_{D1}\) 是设计谱响应加速度参数在一个周期 1.0 s
- \({小号}_{1}\) 是考虑的地震谱响应加速度参数的映射最大值
- \({小号}_{DS}\)是短周期范围内的设计谱响应加速度参数
- \({Ť}_{大号}\) 是长期过渡期
数字 3. USGS 地震设计网络服务.
为了请求上述数据，我们将需要以下数据:
- 纬度, 我们可以从谷歌地图获得的经度
- 基于部分的结构的风险类别 1.5 ASCE的 7-16
- 基于表的站点类 20.3-1 ASCE的 7-16
等效侧向力程序
抗震设计基础剪力可以使用公式计算 12.8-1 ASCE的 7-16:
\( V = {C}_{小号} w ^ \) (情商. 12.8-1)
在哪里:
\( V \) 是抗震设计基础剪力
\( {C}_{s} \) 是基于截面的地震反应系数 12.8.1.1
\( w ^ \) 是根据截面的有效抗震重量 12.7.2
确定地震反应系数的公式为:
\( {C}_{s} = frac{{小号}_{DS}}{ \压裂 { [R }{ {一世}_{Ë} } } \) (情商. 12.8-2)
在哪里:
\( {小号}_{DS} \) 是短周期范围内的设计谱响应加速度参数 (来自美国地质调查局数据)
\( [R \) 是表中的响应修正因子 12.2-1
\( {一世}_{Ë} \) 是从截面确定的重要性因子 11.5.1
然而, 我们需要满足方程 12.8-3 至 12.8-6:
是屋檐到屋脊的水平距离 \({C}_{s}\) 不应超过 12.8-3 要么 12.8-4
对于 \( T ≤ {Ť}_{大号}\):
\({C}_{s,最高} = frac { {小号}_{D1}}{ \压裂{T R}{{一世}_{Ë}}} \) (情商. 12.8-3)
对于 \( Ť > {Ť}_{大号}\) :
\({C}_{s,最高} = frac { {小号}_{D1} {Ť}_{大号} }{ \压裂{ {Ť}^{2} [R}{{一世}_{Ë}}} \) (情商. 12.8-4)
此外, \( {C}_{s} \) 不得小于等式 12.8-5
\( {C}_{s,分} = 0.044 {小号}_{DS} {一世}_{Ë} ≥ 0.01 \) (情商. 12.8-5)
此外, 对于位于的结构 \( {小号}_{1} ≥0.6g):
\( {C}_{s,分} = 0.5 \压裂 {{小号}_{1}} { \压裂{[R}{{一世}_{Ë}}} \) (情商. 12.8-6)
在哪里
\( {小号}_{D1} \) 是在周期的设计谱响应加速度参数 1.0 s (来自美国地质调查局数据)
\( Ť \) 是结构的基本周期
\( {Ť}_{大号} \) 是长期过渡期 (来自美国地质调查局数据)
\( {小号}_{1} \) 是映射的最大考虑地震谱响应加速度参数 (来自美国地质调查局数据)
一旦我们计算出抗震设计基础剪力值 \( V \), 我们需要使用截面沿结构的高度分布力 12.8.3 ASCE的 7-16. 在这个例子中, 我们将假设该结构没有垂直或水平不规则性.
\( {F}_{X} ={C}_{vx} V \) (情商. 12.8-11)
\( {C}_{vx} = frac {{w}_{X}{{H}_{X}}^{ķ}} { \和_{i = 1}^n{w}_{一世}{{H}_{一世}}^{ķ}} \) (情商. 12.8-12)
在哪里
\( {C}_{vx} \) 是垂直分布因子
\( {w}_{一世} \) 和 \( {w}_{X} \) 是结构总有效抗震重量的一部分 \( w ^ \) 位于或分配到级别 一世 要么 X
\( {H}_{一世} \) 和 \( {H}_{X} \) 是从底座到水平的高度 一世 要么 X
\( ķ \) 定义如下:
- \( k = 1 \) 对于结构 \( T ≤ 0.5 s)
- \( k = 2 \) 对于结构 \( ≥ 2.5 s)
- 的线性插值 \( ķ \) 对于 \( 0.5 < Ť < 2.5 s \)
此外, 地板和屋顶隔膜力可以使用截面来确定 12.10.1 ASCE的 7-16. 可以使用方程式计算设计力 12.10-1 至 12.10-3:
\( {F}_{像素} = 分数 { \和_{我=x}^n {F}_{一世}} { \和_{我=x}^n {w}_{一世} }{w}_{像素} \) (情商. 12.10-1)
\( {F}_{像素,分} = 0.2 {小号}_{DS}{一世}_{Ë}{w}_{像素} \) (情商. 12.10-2)
\( {F}_{像素,最高} = 0.4 {小号}_{DS}{一世}_{Ë}{w}_{像素} \) (情商. 12.10-3)
在哪里
\( {F}_{像素} \) 是水平的隔膜设计力 X
\( {F}_{一世} \) 是施加在水平面上的设计力 一世
\( {w}_{一世} \) 是水平的权重支流 一世
\( {w}_{像素} \) 是水平隔膜的重量支流 X
我们将在下面深入研究这些参数并将这个概念应用到我们的结构中.
重要性因子, \( {一世}_{Ë} \)
重要因素, \( {一世}_{Ë} \), 对于结构可以从部分确定 11.5.1 指向表 1.5-2 ASCE的 7-16.
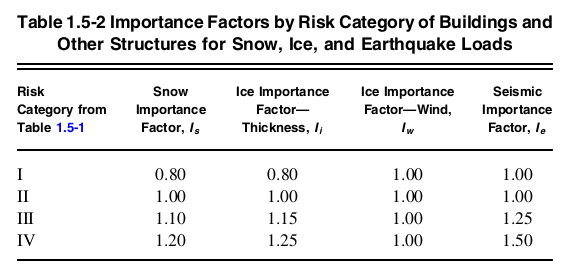
数字 4. 桌子 1.5-2 ASCE的 7-16 指示每个风险类别的重要性因子值.
由于该结构属于 风险类别 II, 相应的重要性因子 \( 一世_{Ë} \) 等于 1.0 基于表 1.5-2.
\( {一世}_{Ë} = 1.0 \)
响应修正因子, \( [R \)
响应修正因子, \( [R \), 雪地装载 12.2-1 取决于使用的结构系统. 在这个例子中, 我们将假设使用的结构系统是 “特殊钢筋混凝土弯矩框架” 对于 X 和 Z 方向. 由此, 我们可以确定 \( [R \) 等于 8 根据表 12.2-1.
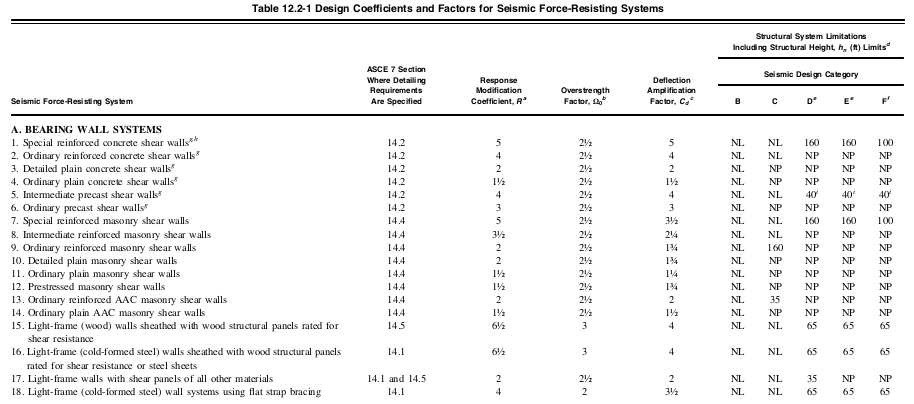
数字 5. 表的截断值 12.2-1 ASCE的 7-16 表示响应修正系数, \( [R \), 每个结构系统.
站点类
计算我们的地震荷载, 我们将使用的位置是 罗利山, 波特兰, 要么, 美国 基于地震载荷: ASCE 地震荷载规定指南 7-16 (查尼等人。, 2020) 分类为 站点 C 类.
美国地质勘探局地震数据
.该位置的 USGS 地震数据如下:
SkyCiv 现在集成了来自 USGS Web API 的现场地震数据. 试试我们的 SkyCiv负载生成器!
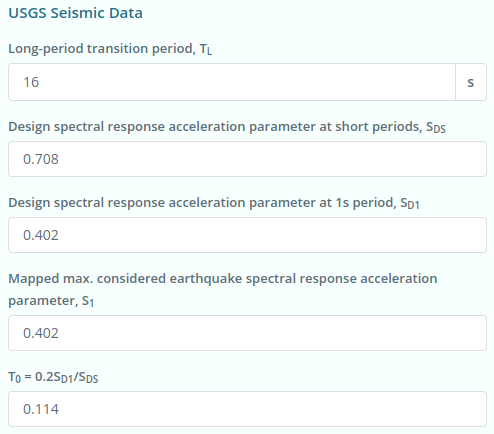
数字 6. 来自 USGS 网络服务的现场地震数据.
\({小号}_{D1} = 0.402 \)
\({小号}_{1} = 0.402 \)
\({小号}_{DS} = 0.708 \)
\({Ť}_{大号} = 16 s \)
\({Ť}_{0} = 0.114 \)
抗震设计类别
部分 11.6 ASCE的 7-16 详细说明如何根据结构的风险类别和场地等级确定结构的抗震设计类别的程序.
- 对于 \({小号}_{1} ≥ 0.75 \) 和风险类别 I, II, 或 III, 抗震设计类别应分配给抗震设计类别 E
- 对于 \({小号}_{1} ≥ 0.75 \) 和风险类别 IV, 抗震设计类别应分配给抗震设计类别 F
- 除此以外, 桌子 11.6-1 和表 11.6-2 应使用, 以较严重者为准.
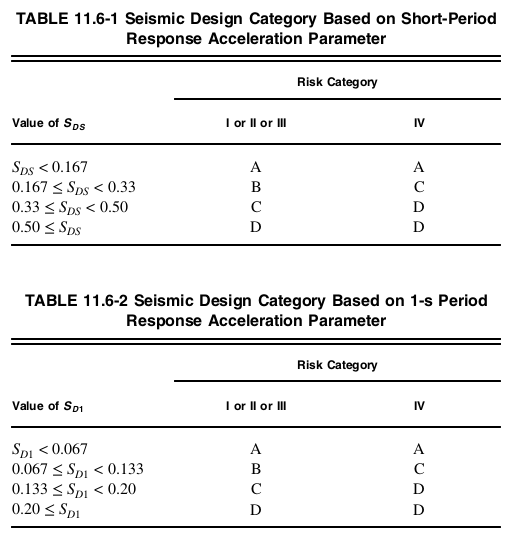
数字 7. Section 的抗震设计类别 11.6 ASCE的 7-16.
对于这种结构, 风险类别 II, \({小号}_{D1} = 0.402 \), 和 \({小号}_{DS} = 0.708 \) 基于两个表，抗震设计类别为 D 11.6-1 和 11.6-2 ASCE的 7-16. 抗震设计类别将用于冗余系数 \( r \) 在计算隔膜设计力时.
结构的基本时期 \( Ť \)
结构的基本周期可以从结构的模态分析中确定. 协会 7-16 允许使用截面近似结构的基本周期 12.8.2.1.
\( {Ť}_{一个} = {C}_{Ť} {{H}_{ñ}}^{X} \)
在哪里 \( {H}_{ñ} \) 是结构的结构高度 (基础至结构抗震系统最高层的垂直距离), 和 \( {C}_{Ť} \) 和 \( X \) 雪地装载 12.8-2.
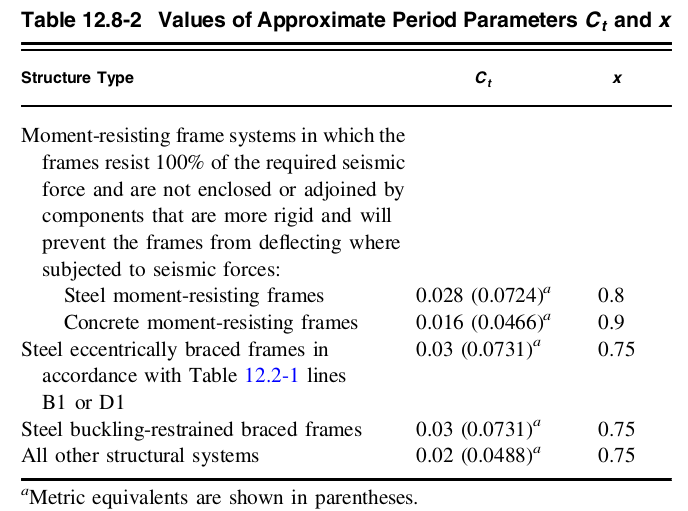
数字 8. 的价值 \( {C}_{Ť} \) 和 \( X \) 从表 12.8-2 ASCE的 7-16.
由于结构是混凝土抗弯框架:
\( {C}_{Ť} = 0.016\)
\( x = 0.9\)
因此, 使用结构高度 \( {H}_{ñ} \) 我们将插入已知值 75 英尺。, 结构的近似基本周期 \( {Ť}_{一个} \) 可以确定:
\( {Ť}_{一个} = {C}_{Ť} {{H}_{ñ}}^{X} = (0.016) {(75)}^{0.9}\)
\( T = {Ť}_{一个} = 0.7792 s)
地震反应系数 \({C}_{s}\)
因为屋顶轮廓是山墙或双坡, 我们已经可以计算地震响应系数 \({C}_{s}\):
\( {C}_{s} = frac{ {小号}_{DS} }{ \压裂 {[R}{{一世}_{Ë}} } = frac{ 0.402 }{ \压裂 {8}{1.0} } \)
\( {C}_{s} = 0.0885\)
以来 \( T ≤ {Ť}_{大号}\):
\({C}_{s,最高} = frac { {小号}_{D1}}{ \压裂{T R}{{一世}_{Ë}}} = frac { (0.402)}{ \压裂{(0.7792)(8)}{(1.0)}} \)
\({C}_{s,最高} = 0.0645 \)
此外, 的最小值 \( {C}_{s} \) 不得少于:
\( {C}_{s,分} = 0.044 {小号}_{DS} {一世}_{Ë} ≥ 0.01 \)
\( {C}_{s,分} = 0.044 (0.402) (1.0) ≥ 0.01 \)
\( {C}_{s,分} = 0.0312 \)
的最终值 \( {C}_{s} \) 用于计算的应为:
\( {C}_{s} = 0.0645\)
有效抗震重量 \( w ^ \)
在这个例子中, 我们将使用施加在地板上的恒载和叠加恒载来计算有效抗震重量. 假定外墙和内墙包含在叠加楼板恒载中，等于 100 psf. 使用混凝土单位重量等于 156 磅/立方英尺:
对于典型的楼层 (不包括地面和屋顶水平):
柱: 典型层高 x 横截面积 x 混凝土单位重量 x 总数. 列数 = 15 英尺 x 156 磅/立方英尺. X (20″x20″) X 35 = 227.5 ps
大板: 建筑面积 x 厚度 x 混凝土单位重量 = 64 英尺 (104 英尺) × 8″ X 156 磅/立方英尺. = 692.224 ps
横梁: 混凝土总长 x 横截面积 x 单位重量 = 968 英尺 x 156 磅/立方英尺. X (14″x20″) = 293.627 ps
叠加恒载: 楼面面积 x 负载 = 64 英尺 (104 英尺) X 100 psf= 665.6 ps
每层总静载: 1878.951 ps
对于屋顶水平:
柱: 典型层高 x 横截面积 x 混凝土单位重量 x 总数. 列数 = 7.5 英尺 x 156 磅/立方英尺. X (20″x20″) X 35 = 113.75 ps
大板: 建筑面积 x 厚度 x 混凝土单位重量 = 64 英尺 (104 英尺) × 8″ X 156 磅/立方英尺. = 692.224 ps
横梁: 混凝土总长 x 横截面积 x 单位重量 = 968 英尺 x 156 磅/立方英尺. X (14″x20″) = 293.627 ps
叠加恒载: 楼面面积 x 负载 = 64 英尺 (104 英尺) X 50 psf= 332.8 ps
屋顶平面的总恒载: 1432.401 ps
综上所述:
| 楼层 | 海拔, 英尺 | 重量, wx, ps |
| 屋顶 | 75 | 1432.401 |
| 5级别 | 60 | 1878.951 |
| 4级别 | 45 | 1878.951 |
| 3研发水平 | 30 | 1878.951 |
| 2第 2 级 | 15 | 1878.951 |
| 有效抗震重量, w ^ | 8948.203 | |
\( 是屋檐到屋脊的水平距离 8949.203 基普)
地震底剪 \( V \)
使用方程式 12.8-1 ASCE的 7-16, 可以计算地震基础剪力:
\( V = {C}_{小号} 是屋檐到屋脊的水平距离 (0.0645)(8948.203) \)
\( V = 577.159 ps \)
地震力的垂直分布 \( {F}_{X} \)
我们需要将地震荷载分布在整个结构中. 由于结构的基本周期是 \( T = {Ť}_{一个} = 0.7792 s), 因此:
\( k = 1.1396\)
计算地震力 \( {F}_{X} \) 每级, 最好的方法是将每个级别的地震权重制成表格:
| 楼层 | \( {w}_{X} \) ps | \( {H}_{X} \) 英尺 | \( {w}_{X} {{H}_{X}}^{ķ} \) | \( {C}_{vx} \) |
\( {F}_{X} \) ps |
| 屋顶 | 1432.401 | 75 | 196303.644 | 0.2923 | 168.6950 |
| 5级别 | 1878.951 | 60 | 199681.715 | 0.2973 | 171.5980 |
| 4级别 | 1878.951 | 45 | 143865.010 | 0.2142 | 123.6315 |
| 3研发水平 | 1878.951 | 30 | 90631.141 | 0.1349 | 77.8845 |
| 2第 2 级 | 1878.951 | 15 | 41135.482 | 0.0612 | 35.3501 |
| 小号 = 671616.992 | \( V \) = 577.1591 |
隔膜力 \( {F}_{像素} \)
隔膜力的计算如下所示. 因为我们假设没有违规行为, 冗余因子 \( r \) 设定为 1.0. 该参数应乘以 \( {F}_{像素} \):
| 楼层 | \( {w}_{像素} \) ps | \( Σ {w}_{一世} \) |
\( Σ {F}_{一世} \) | \( {F}_{像素,分} \) | \( {F}_{像素,最高} \) | \( {F}_{像素} \) | 设计 \( {F}_{像素} \) |
| 屋顶 | 1432.401 | 1432.401 | 168.6950 | 202.8279 | 405.6559 | 168.6950 | 202.8279 |
| 5级别 | 1878.951 | 3311.351 | 340.2930 | 266.0594 | 532.1188 | 193.0915 | 266.0594 |
| 4级别 | 1878.951 | 5190.302 | 463.9245 | 266.0594 | 532.1188 | 167.9461 | 266.0594 |
| 3研发水平 | 1878.951 | 7069.253 | 541.8090 | 266.0594 | 532.1188 | 144.0085 | 266.0594 |
| 2第 2 级 | 1878.951 | 8948.203 | 577.1591 | 266.0594 | 532.1188 | 121.1923 |
266.0594 |
SkyCiv负载生成器
所有这些计算都已包含在 SkyCiv 负载生成器中. 使用我们用于 ASCE 的免费地震载荷计算器简化您的计算 7-16!
现场地震数据
USGS 地震数据可在风险类别下获得, 站点类, 和项目地址已定义. 注意参数 \({小号}_{D1} \), \({小号}_{1} \), \({小号}_{DS} \), 和 \({Ť}_{大号} \) 应该有值才能继续进行地震载荷计算.
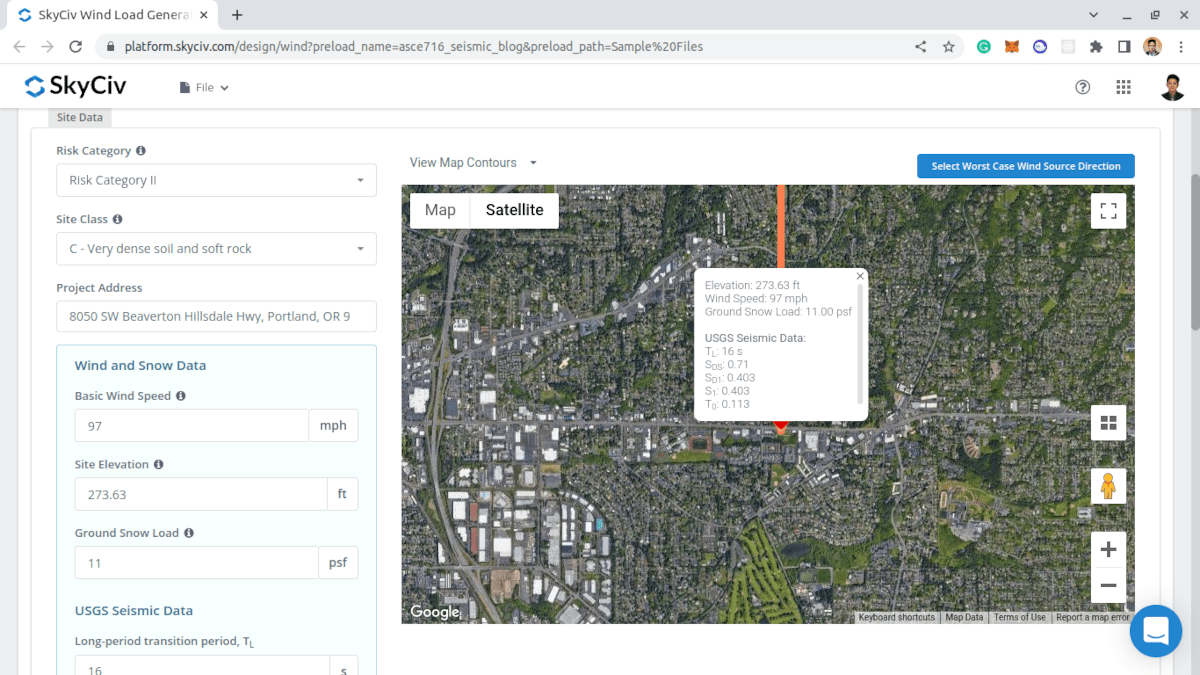数字 9. 获取该位置的 USGS 地震数据所需的参数.
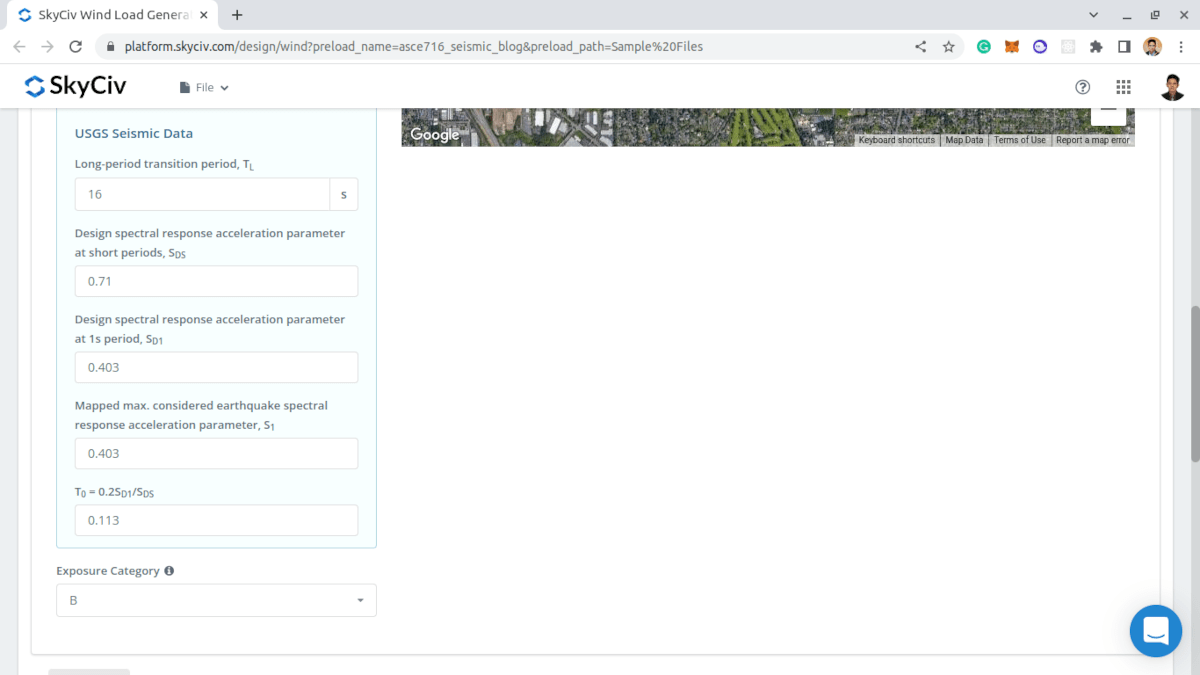
数字 9. 美国地质勘探局地震数据的结果.
用户可以修改从 USGS Web Services 获得的参数，以获得最适合结构的地震荷载.
结构数据
在结构数据选项卡上, 您只需要定义标准的建筑数据: 屋顶型材, 建筑长度, 建筑宽度, 平均屋顶高度, 和屋顶俯仰角.
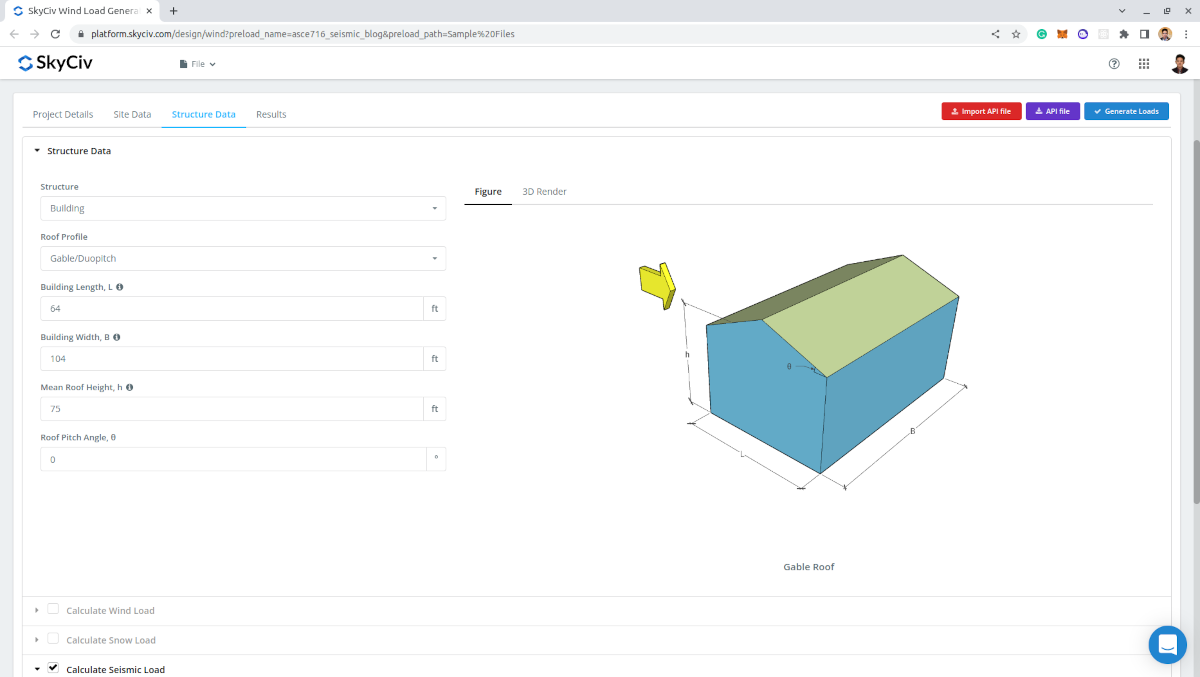
数字 10. 建筑数据输入.
地震数据
继续进行地震计算, 所需内容如下:
- 结构系统 – 用于确定的值 \({C}_{Ť} \) 和 \(X \) 这将用于计算结构的近似基本周期 \({Ť}_{一个} \)
- 结构的近似基本周期 \({Ť}_{一个} \) – 可以用户自定义更合适的地震荷载计算
- 响应修正因子 \( [R \) – 默认值为 8.5 并进行修改以获得更合适的地震结果
- 冗余系数, \( r \) – 默认值为 1.0 并且可以修改. 用于隔膜力计算
- 地板重量 – 用于基础剪力的垂直分布和隔膜力. 所需的每个级别的数据是: 我们已经可以解决设计风速 (用于指定), 海拔, 和重量
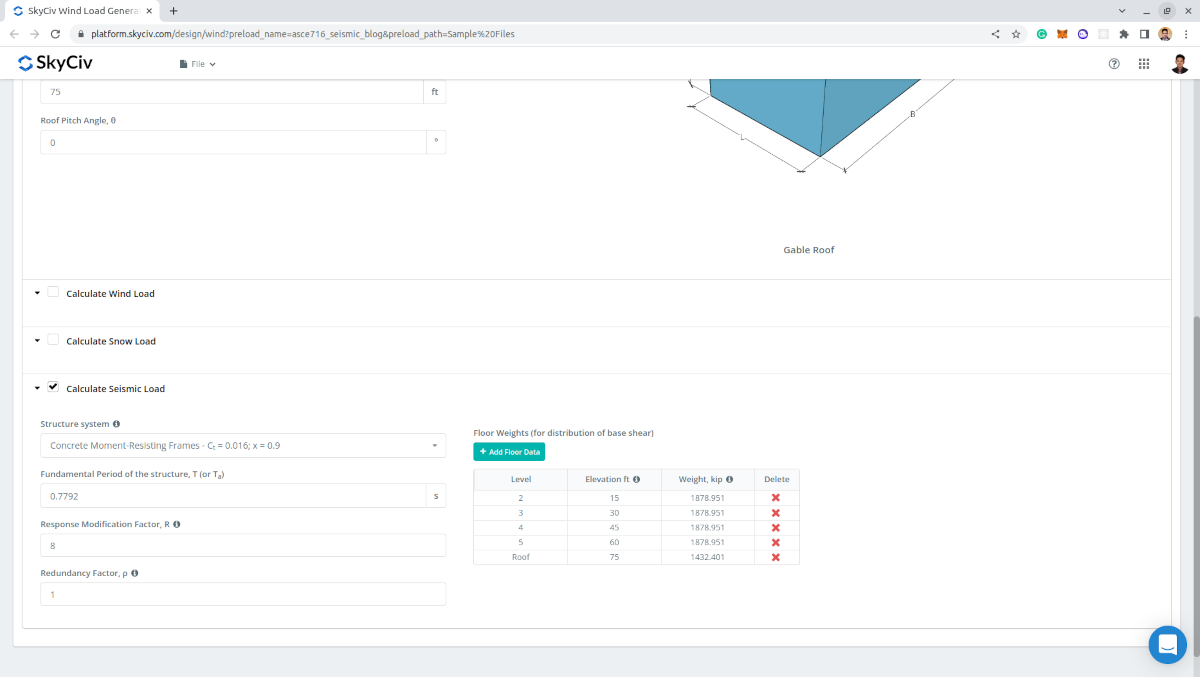
数字 11. 地震计算所需的地震参数.
结果
计算的输出是使用的地震参数和计算的地震基础剪力 \(V \), 每层地震力, 和每层的隔膜力.
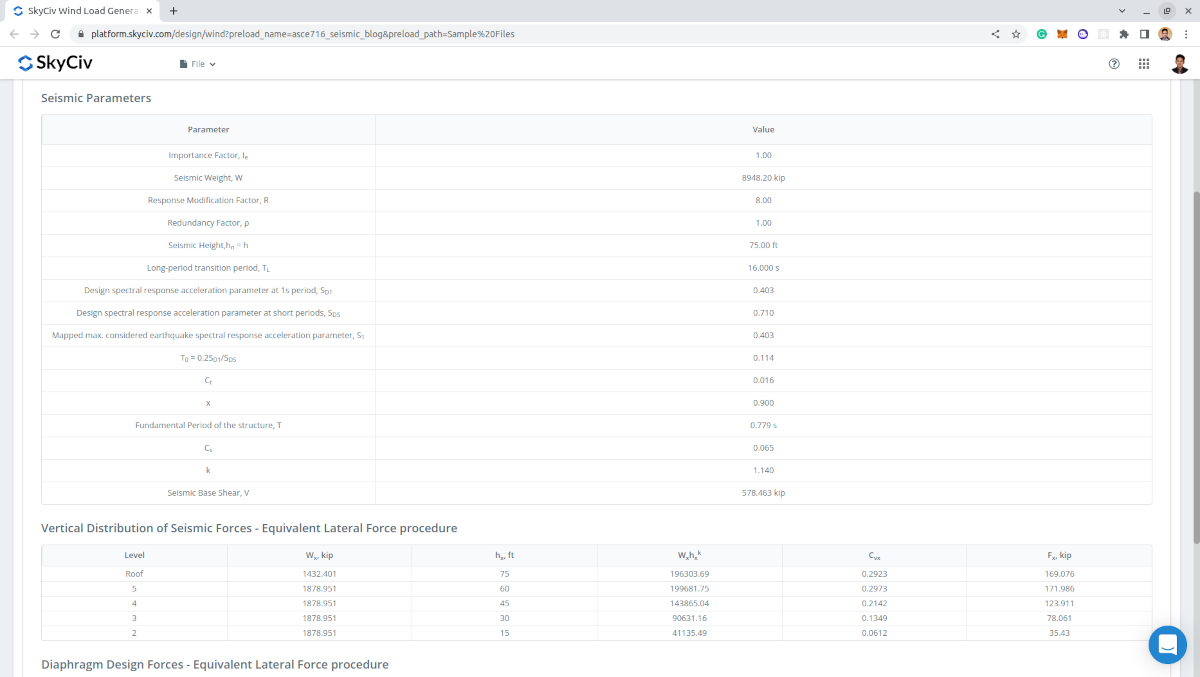
数字 12. 地震荷载计算的输入参数和结果.
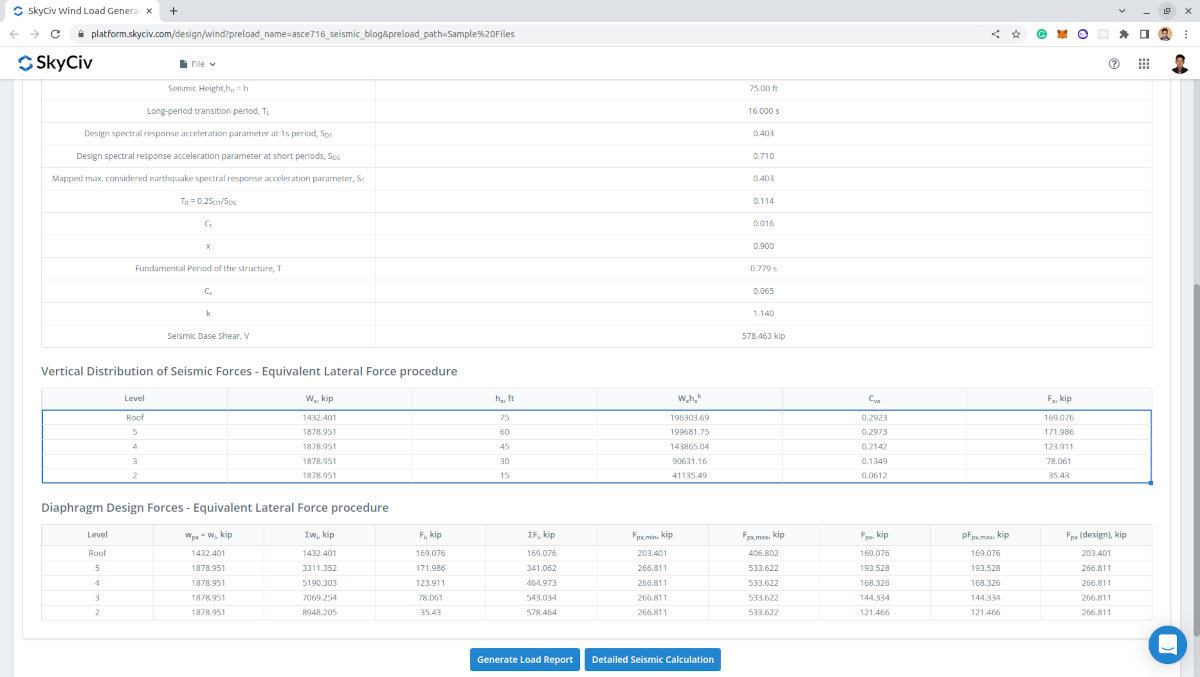
数字 13. 每层的地震力列表，包括隔膜设计力.
详细报告
生成结果时, 专业帐户用户 和那些购买了 独立负载生成器模块 可以生成详细的地震计算. 该报告显示地震计算中使用的所有参数和假设，以使其对用户透明. 可以通过此访问为该示例计算生成的报告 链接.
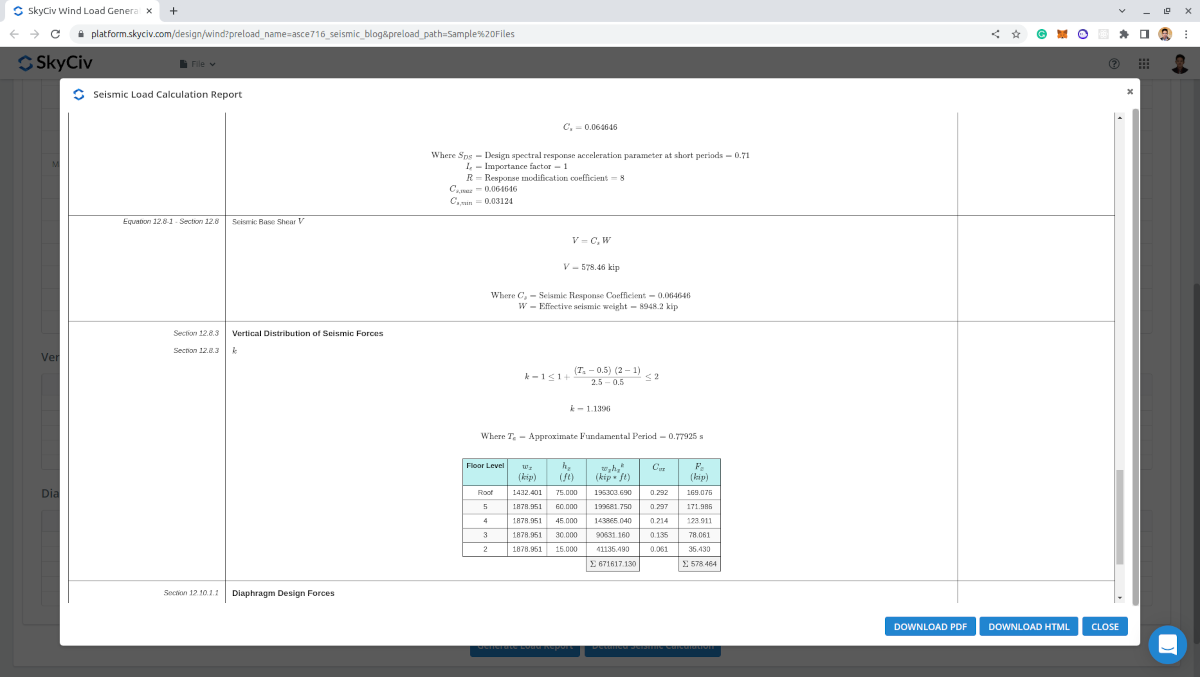
数字 14. SkyCiv Load Generator的详细地震荷载计算.
通过以下方式利用此功能 注册专业帐户 或通过购买 独立的Load Generator模块! 对于现有用户, 一个 免费演示 如果您需要更全面的负载计算解决方案，也可以使用.
有关其他资源, 你可以通过这个查看我们的 API 文档:
结构工程师, 产品开发
土木工程硕士
领英
参考资料:
- 美国土木工程师学会. (2017, 六月). 建筑物和其他结构的最小设计载荷和相关标准. 美国土木工程师学会.
- 查尼, F。, 豪斯勒, T。, 和马歇尔, Ĵ. (2020). 地震载荷: ASCE 地震荷载规定指南 7-16. 美国土木工程师学会.
- 你可以通过这个查看我们的 API 文档
