如何计算不确定的光束 – 双积分法

不定 横梁 可能是一个挑战，因为解决反应需要额外的步骤. 请记住，不确定结构具有所谓的不确定度. 解决结构, 必须引入边界条件. 所以, 不确定程度越高, 需要识别的边界条件越多. 但在我们解决不确定梁之前, 我们首先需要确定梁是否是静态不确定的. 由于梁是一维结构, 使用该方程来确定外部超静定结构就足够了.

[数学]
一世_{Ë}=R-左 ( 3+e_{C} \对 )
[数学]

在哪里:

• 一世_Ë = 不确定度
• R = 反应总数
• Ë_C = 外部条件 (例如. 内铰链)

通常, 然而, 无需求解不确定度, 除了简单的跨度或悬臂梁之外的任何东西都是静态不确定的, 假设这样的梁没有内部铰链.

有很多方法可以解决不确定梁的问题. 尽管为了简单起见并与 SkyCiv Beam 相似 手工计算, 我们将讨论双重积分方法.

双积分

双积分可能是所有梁分析方法中最简单的. 与其他方法相比，该方法的概念非常简单，因为它主要依赖于对积分微积分的基本理解, 由此得名. 从梁的曲率与力矩的关系中改编了一些积分，如下所示.

[数学]
\压裂{1}{\罗}= 分数{中号}{不}
[数学]

请注意，1/ρ 是梁的曲率，ρ 是曲线的半径. 从根本上, 曲率的定义是切线相对于弧长的变化率. 由于力矩是相对于构件长度的载荷的函数, 将曲率相对于构件的长度积分将产生梁的斜率. 相似地, 将斜率相对于构件的长度积分将产生梁偏转. 由于典型的结构载荷本质上是代数的, 这些表达式的积分就像使用通用幂公式一样简单.

[数学]
\整数 f左 ( x 右 )^{ñ}dx=frac{f左 ( x 右 )^{n+1}}{n+1}+C
[数学]

也许理解这个概念的最好方法是提供一个光束的例子，下面给出.

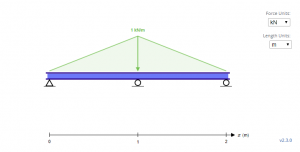
上面的示例梁是一个带有三角形载荷的不确定梁. 随着 支持, 一个_和, 乙_和 和 C_和 为了第一, 第二, 和第三个分别支持, 求解这些未知数的第一步是从平衡方程开始.

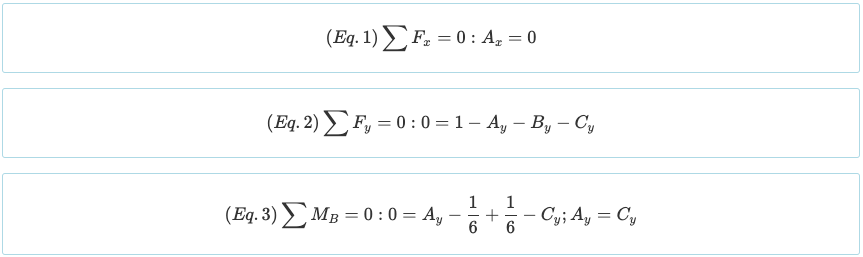
请注意，梁的度数为 静不确定性 1°. 因为有四个未知数 (一个_X, 一个_和, 乙_和, 和 C_和) 到目前为止，除了上面的平衡方程之外，还有三个方程, 有必要根据边界条件再创建一个方程. 回想一下，点载荷和三角载荷产生的力矩如下.

点载荷:

[数学]
M=Ftimes x; M = Fx
[数学]

三角荷载:

[数学]
M=frac{w_{0}\x 次}{2}\时代左 ( \压裂{X}{3} \对 ); M = frac{w_{0}x^{2}}{6}
[数学]

使用双重积分法, 这些新方程被制作并显示在下面.

注意: 上面的方程被写成麦考利函数，其中一个表达式等于 0，当 X < 大号. 在这种情况下, L = 1.

在上面的等式中, 请注意，添加的第四个术语似乎无处不在. 事实上, 加载方向与重力方向相反. 这是因为三角形载荷方程仅在载荷随着长度增加而上升时才起作用. 这对于方程来说不是什么大问题 分散式 和 点荷载 由于它们的对称性. 有效, 上面梁的等效载荷看起来像下面的梁, 因此方程基于它.

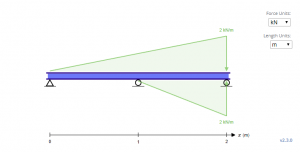
求解 C₁ 和 C₂, 必须确定边界条件. 在上面的梁, 可以观察到，三个这样的边界条件存在于 X = 0, X = 1, 和 X = 2, 其中三个位置的挠度 y 为零.

边界条件 1

[数学]
x=0, y = 0; C_{2}= 0
[数学]

边界条件 2

[数学]
x=0, y = 0; C_{1}= 分数{1}{120}-\压裂{一个_{和}}{6}
[数学]

确定每个常数的值后, 现在可以使用最后一个边界条件获得最后一个方程.

边界条件 3

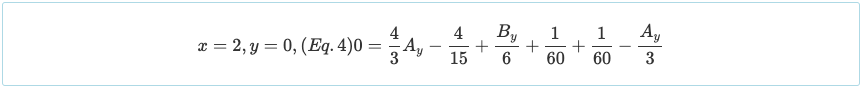
注意θ的边界条件= 0 在x = 1 可以使用, 虽然只适用于对称荷载的对称连续梁的中间反力.

由于已经确定了四个方程, 它们现在可以同时解决. 求解这些方程将产生以下反应.

随着反应确定, 反应的值可以代回力矩方程. 这将使我们能够确定梁系统任何部分的力矩值.

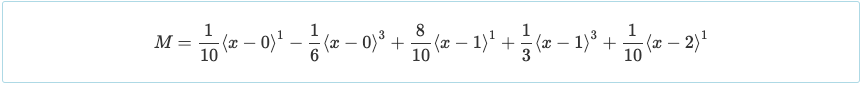
双积分的另一个便利是力矩方程的表示方式可用于求解剪切，其关系如下所示.

[数学]
V = 压裂{米}{dx}
[数学]

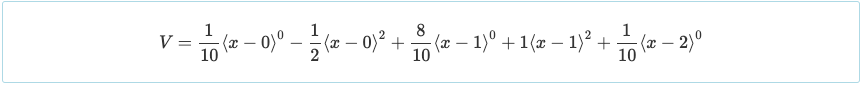
再次, 仅使用对微分的基本了解, 将函数的导数等于零会产生该函数的最大值或最小值. 从而, 等于 V = 0 将导致最大的正时刻 X = 0.447 和 X = 1.553 M = 0.030

当然, 所有这些都可以通过 SkyCiv Beam 进行验证.

SkyCiv Beam软件

SkyCiv 光束分析软件 允许用户轻松准确地分析梁结构. 你可以得到你的梁成员的分析, 包含 反应, 剪力, 弯矩, 偏转, 和 压力 在几秒钟内.

如果你想先试一试, 自由光束计算器 是一个很好的开始方式, 或者今天就免费注册!