总览
弯曲应力是结构设计中最重要的值之一, 对于大多数水平梁而言,这通常是关键或控制设计. 当水平梁加载时, 它产生 弯矩 该部分的顶部和底部纤维中的应力可能会使该部分承受过大的应力,导致其屈服或完全失效.
计算弯曲应力时, 考虑以下因素很重要:
- 截面的转动惯量 – 直接影响弯曲应力
- 您正在检查横梁上的哪个位置 – 远离截面中性轴时,弯曲应力通常会增加 (因此,为什么截面顶部和底部的应力最大)
- 材料特性 – 更强的材料 (例如更高的屈服强度) 可以承受更高的应力,可能更适合某些设计
- 横截面形状 – 与点一样 (1) 以上 – 不同的截面非常适合承受更高的弯曲应力, 鉴于其较高的转动惯量值
- 应力方向 – 根据载荷的方向,弯曲可能发生在截面的长轴/短轴上.
- 经常, 这些弯曲应力可以与剪切应力或轴向应力相结合 (由于其他方向的力), 增加梁的总应力
在下面的指南中我们将主要探讨如何计算弯曲应力 (特别是在工字梁中), 但在学习这些原则时,记住上述背景很重要.
如何计算梁的弯曲应力?
了解弯曲应力很重要,因为梁弯曲在梁设计中起着至关重要的作用. 本教程将介绍如何使用公式计算梁中的弯曲应力. 该公式将梁中的纵向应力分布与内部 弯矩 作用于梁的横截面. 我们假设光束的材料是 线弹性 (即. 胡克定律 适用).
1. 使用弯曲应力公式手动计算弯曲应力 (方程)
让我们看一个例子. 考虑下面显示的工字梁:
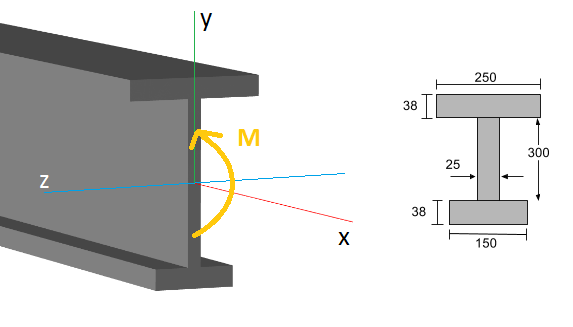
在沿梁长度的特定点 (x轴), 存在内部弯矩 (m), 通常使用弯矩图确定. 一般弯曲应力公式 (或正常压力) 该部分是:

考虑梁的特定部分时, 很明显,弯曲应力将在距中性轴特定距离处达到其最大值 (和). 从而, 最大弯曲应力将出现在梁截面的顶部或底部, 取决于哪个距离更大:
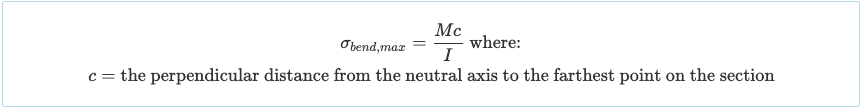
让我们考虑上面显示的工字梁的真实示例. 在我们之前的 惯性矩教程, 我们已经发现绕中性轴的惯性矩为I = 4.74×108 毫米4. 另外, 在里面 重心教程, 我们找到了质心,因此找到了中性轴的位置 216.29 距截面底部的毫米. 如下所示:
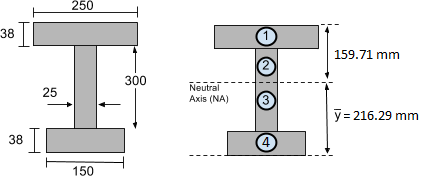
通常需要确定截面承受的最大弯曲应力. 例如, 假设我们已经确定, 从弯矩图, 梁遇到的最大弯矩为 50 kN-m或 50,000 牛顿米 (转换弯矩单位后).
然后我们需要找到截面的顶部或底部是否离中性轴更远. 清楚地, 该部分的底部有更大的距离, 测量 c = 216.29 毫米. 有了这些信息, 我们可以使用上面提供的弯曲应力公式来计算最大应力:

相似地, 我们可以在该部分的顶部找到弯曲应力, 我们知道它是y = 159.71 距中性轴毫米 (不适用):

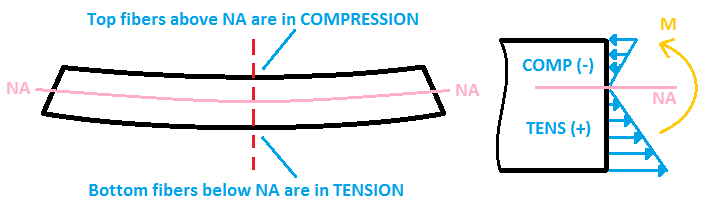
最后的考虑包括确定梁应力是否导致截面纤维的压缩或拉伸.
- 如果梁下垂像 “ü” 形状, 顶部纤维受到压缩 (负压力), 而底部纤维承受张力 (正压力).
- 如果光束倒置下垂 “ü” 形状, 形势逆转: 底部纤维受到压缩, 而顶部纤维会受到拉力.
2. 使用软件计算弯曲应力
上节讨论了手算的弯曲应力公式, 但您不再需要自己手动完成 SkyCiv Beam计算器 只需单击一下即可帮助您找到梁中的剪切应力和弯曲应力. 通过简单地对梁建模, 纳入支持, 并施加负载, 您可以使用此弯曲应力计算器获得最大应力. 下图显示了I型梁承受弯曲应力的示例:
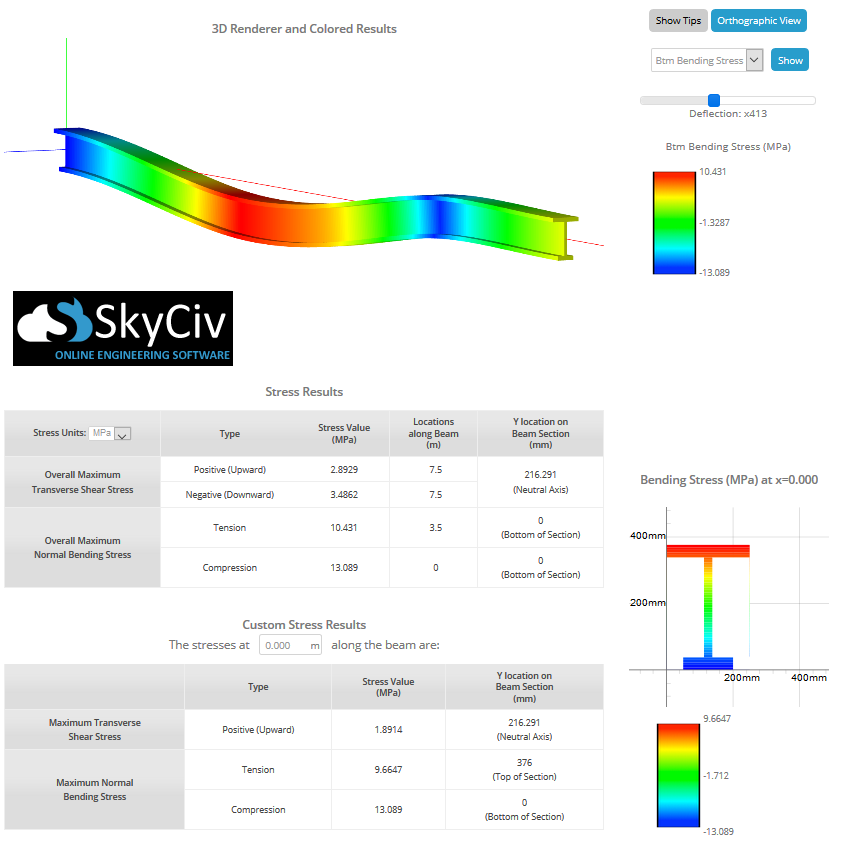
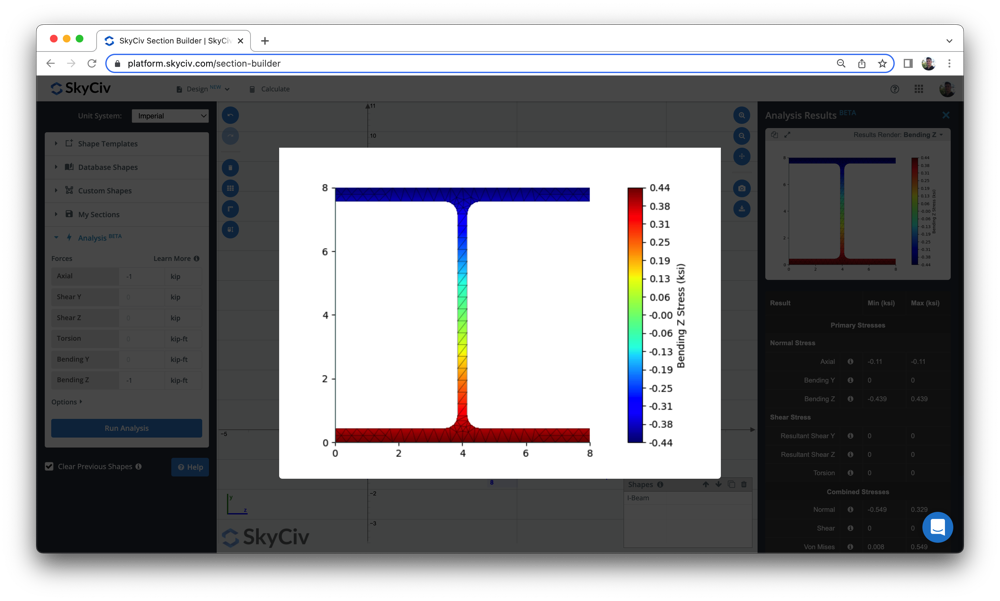
用户还可以使用以下 梁应力软件 计算弯曲应力和其他梁应力, 使用简单的部分构建工具. 因此,请查看我们上面的光束工具或立即注册免费体验该软件!
更多光束文档, 访问我们的文章 计算梁截面的弯曲应力, 如何求弯矩, 确定支撑处的反应, 和 光束偏转.


