惯性矩的基本原理
转动惯量可以导出为 惯性矩 零件和应用转移公式: 我=我0 + 广告2. 我们有一篇全面的文章解释了 求解转动惯量.
从根本上, 惯性矩是区域的第二矩, 可以表示为以下形式:
[数学] 一世_{X}= int int y ^{2}给 [数学] [数学] 一世_{和}= int int x ^{2}给 [数学]
观察以下公式的推导, 我们尝试仅使用上面的公式来找到对象(例如矩形)绕其主轴线的惯性矩. 获得惯性矩, 必须确定极限,以使它们从旋转轴到其极限纤维. 这将是外部积分的极限. 内部积分的极限为 0 到b. 那说, 我们也可以将dA表示为xdy, 这将成为bdy. 由于旋转轴位于中性轴, 惯性矩可以与h / 2的上限和 0 并因矩形的对称性而相乘两次. 这给我们留下了下面的积分.
[数学] 一世_{X}= 2 int_{0}^{\压裂{H}{2}} 和^{2}dy [数学] 整合, [数学] 一世_{X}= 2b 左 [ \压裂{和^{3}}{3} \对 ]_{0}^{\压裂{H}{2}} [数学] [数学] 一世_{X}= 2b 左 [ \压裂{h ^{3}}{24}-0 \对 ] [数学] [数学] 一世_{X}= 分数{bh ^{3}}{12} [数学]
梁截面的惯性矩公式
梁截面的惯性矩公式 (区域的第二时刻). 惯性矩方程对于快速而准确的计算非常有用. 为方便起见,公式已汇总为最简单的形式.
SkyCiv还提供了 惯性矩免费计算器 快速计算或检查您是否正确应用了公式. 矩形的惯性矩公式, 圆圈, 梁截面的惯性矩公式. 梁截面的惯性矩公式:
- 区域惯性矩与质量惯性矩不同
- 这也被称为第二时刻
- 这是变形的重要因素 (我越大X, 较低的挠度将是)
- 单位的长度等于 4
- 下面的方程式给出了相对于截面质心的惯性矩
参考 |
一世xx |
一世y |
矩形或矩形截面的惯性矩矩 |
||
|---|---|---|
 |
[数学] \dfrac{bh ^ 3}{12} [数学] | [数学] \dfrac{b ^{3}H}{12} [数学] |
空心矩形截面惯性方程的矩 |
||
 |
[数学] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [数学] | [数学] \dfrac{b ^ 3小时}{12} – \dfrac{b_1 ^ 3h_1}{12} [数学] |
圆或圆截面的惯性矩矩 |
||
 |
[数学] \dfrac{\pi}{64}D ^ 4 [数学] | [数学] \dfrac{\pi}{64}D ^ 4 [数学] |
空心圆截面惯性方程的矩 |
||
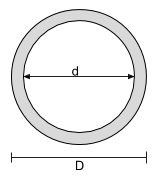 |
[数学] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [数学] | [数学] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [数学] |
等腰三角形的惯性方程的矩 |
||
 |
[数学] \dfrac{bh ^ 3}{36} [数学] | [数学] \dfrac{3b ^ 3小时}{144} [数学] |
I型截面的惯性方程的矩 |
||
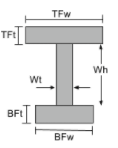 |
[数学] \压裂{TFw times TFt ^{3}}{12} +\压裂{Wt Wh ^{3}}{12} + \压裂{BFw 乘以BFt ^{3}}{12} +[数学] [数学] TFw times TFt times left ( 高炉 + Wh + 分数{TFt}{2} -\酒吧{和}_{机器人} \对 )^{2} +[数学] [数学] Wt timesWh times left ( BFt + 压裂{瓦}{2} -\酒吧{和}_{机器人} \对 )^{2} +[数学] [数学] BFw times BFt times left ( \压裂{瓦}{2} -\酒吧{和}_{机器人} \对 )^{2} [数学] | [数学] \压裂{TFt times TFw ^{3}}{12} + \压裂{Wh 次Wt ^{3}}{12} + \压裂{BFt 乘以BFw ^{3}}{12} [数学] |
T型截面的惯性矩 |
||
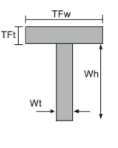 |
[数学] \压裂{TFw times TFt ^{3}}{12} + \压裂{Wt wh Wh ^{3}}{12} +[数学] [数学] TFw times TFt left ( 瓦 + \压裂{TFt}{2} -\酒吧{和}_{机器人} \对 )^{2} +[数学] [数学] Wt times Wh times left ( \压裂{瓦}{2} – \酒吧{和}_{机器人} \对 )^{2} [数学] | [数学] \压裂{TFt 时间TFw ^{3}}{12} + \压裂{Wh times Wt ^{3}}{12} [数学] |
通道截面惯性方程的矩 |
||
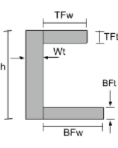 |
[数学] \压裂{TFw times TFt ^{3}}{12} + \压裂{BFw 乘以BFt ^{3}}{12} + \压裂{Wt times h ^{3}}{12} +[数学] [数学] TFw times TFt times left ( H – \压裂{TFt}{2} – \酒吧{和}_{机器人} \对 )^{2} +[数学] [数学] BFw times BFt times left ( \压裂{高炉}{2} – \酒吧{和}_{机器人} \对 )^{2} +[数学] [数学] Wt times h times left ( \压裂{H}{2} – \酒吧{和}_{机器人} \对 )^{2} [数学] | [数学] \压裂{TFt times TFw ^{3}}{12} + \压裂{BFt 乘以BFw ^{3}}{12} + \压裂{h 时间Wt ^{3}}{12} +[数学] [数学] TFt times TFw times left ( Wt + \压裂{TFw}{2} – \酒吧{X}_{剩下} \对 )^{2} +[数学] [数学] BFt times BFw times left ( Wt + \压裂{高炉}{2} – \酒吧{X}_{剩下} \对 )^{2} +[数学] [数学] h times Wt times left ( \压裂{Wt}{2} – \酒吧{X}_{剩下} \对 )^{2} [数学] |
转动惯量角方程 |
||
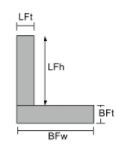 |
[数学] \压裂{BFw 乘以BFt ^{3}}{12} + \压裂{ LFt times LFh ^{3}}{12} +[数学] [数学] BFw times BFt times left ( \压裂{高炉}{2}-\酒吧{和}_{机器人} \对 )^{2} +[数学] [数学] LFt times LFh times left ( 高炉 + \压裂{低频}{2}-\酒吧{和}_{机器人} \对 )^{2} [数学] | [数学] \压裂{BFt 乘以BFw ^{3}}{12} + \压裂{ LFh times LFt ^{3}}{12} +[数学] [数学] BFt times BFw times left ( \压裂{高炉}{2}-\酒吧{X}_{剩下} \对 )^{2} +[数学] [数学] LFh times LFt times left ( \压裂{低频}{2}-\酒吧{X}_{剩下} \对 )^{2} [数学] |
使用SkyCiv Section Builder进行手计算
在这篇文章中, 我们已经向您介绍了惯性矩公式. 有关此主题的更多信息, 请访问我们的教程 梁截面转动惯量.
你知道吗 SkyCiv版块生成器 还显示了以下形状的全手计算?
- 长方形, 空心矩形
- 圆, 空心圆
- 工字梁, 丁字梁
- 角度 (L型钢), 渠道
- 三角形截面
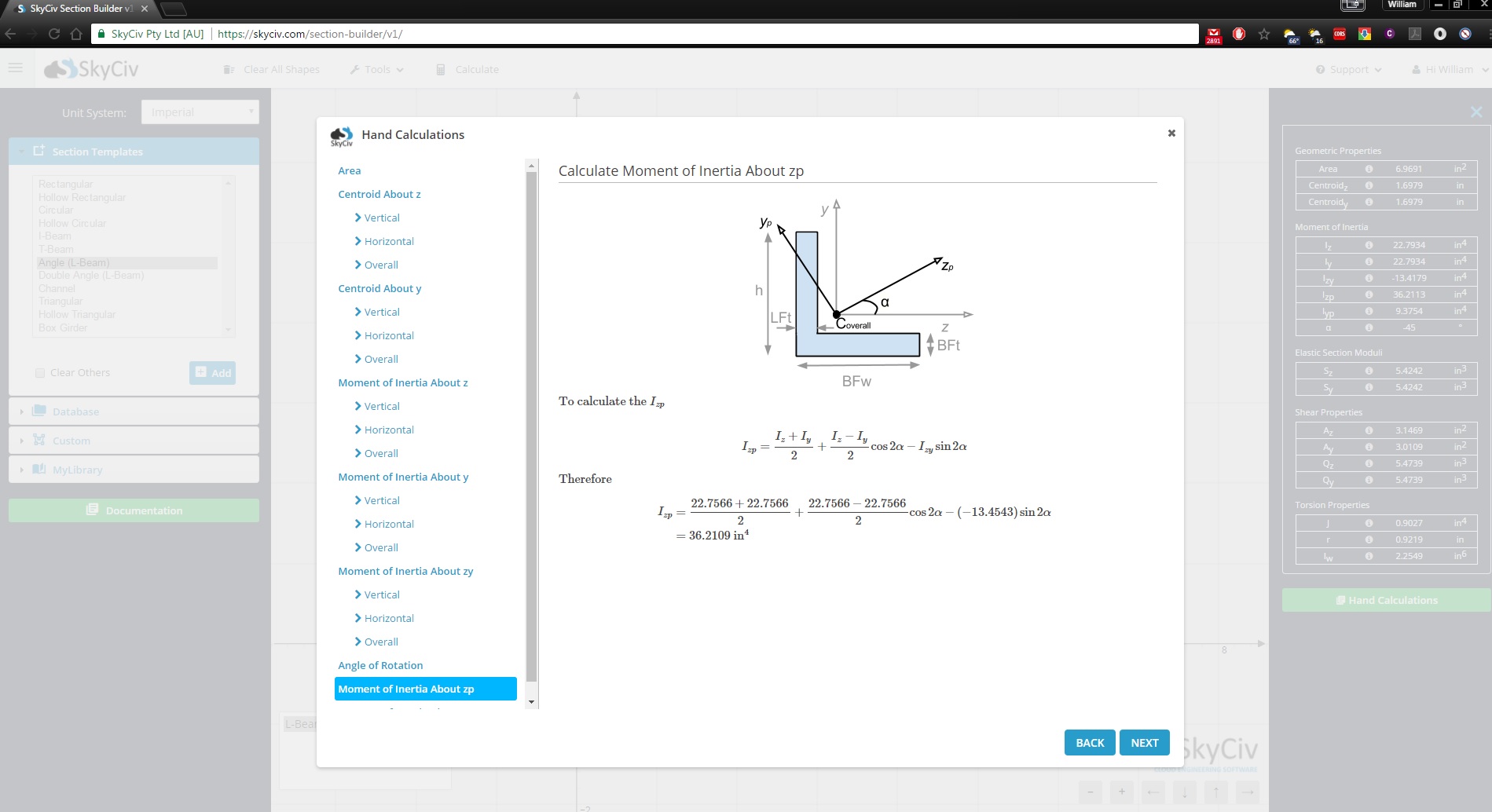
我们希望您发现上表对于如何计算圆的惯性矩很有用, 三角形, 以及其他形状的矩形惯性矩. 我们也有一个有用的 转动惯量计算器, 一个简化的 SkyCiv版块生成器, 为您处理这些计算或立即注册以开始使用 SkyCiv 软件!


