当运行一个 响应谱分析 在结构上, 获得所需结果的最重要步骤之一是定义模态组合方法,软件将使用该方法来获得位移的单一结果, 反应, 内力, 等等… 对于每种振动模式获得的原始结果中的每个自由度 (模态反应). 这些模态组合结果用于设计结构, 这就是为什么正确定义模态组合方法极其重要的原因. 在这篇文章中, 我们将深入研究响应谱分析的一些模态组合方法.
值得一提的是,响应谱分析中最重要的步骤之一是评估每种振动模式的固有频率及其质量贡献, 查看我们关于动态频率分析的文档.
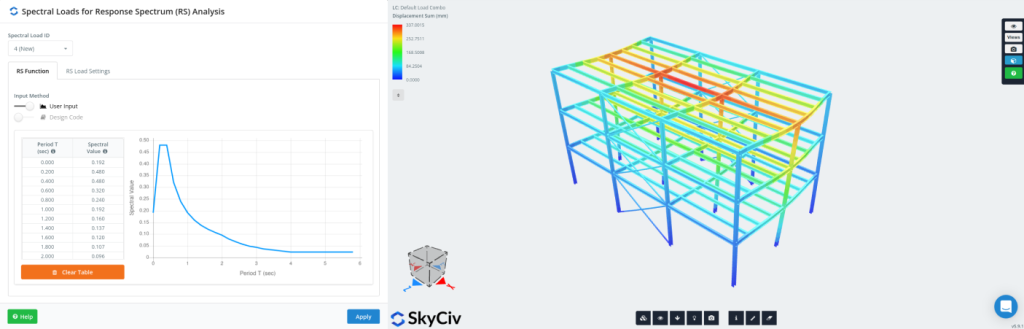
响应谱分析的模态组合方法
一些最著名和使用的模态组合方法是:
- ABS: 绝对和
- SRSS: 平方和的平方根
- 质检总局: 完全二次组合
一般来说, 总响应的峰值 (\(r_o\)) 对于位移, 内力, 反应很有趣. 正如先前所说, 该峰值是通过适当组合峰值模态响应获得的 (\(r_{ñ, 的}\))
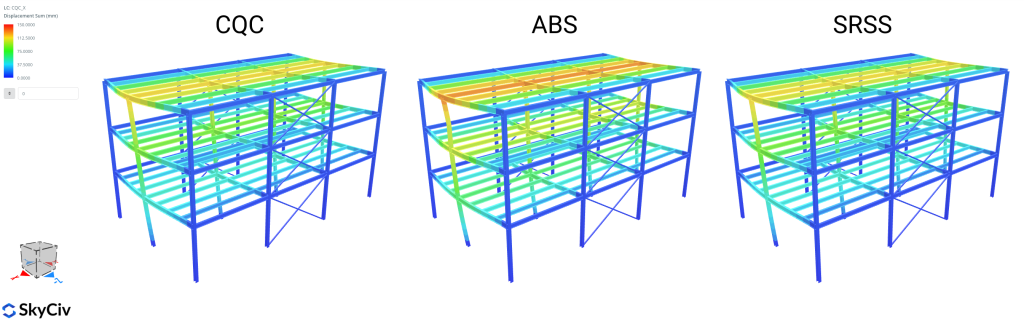
绝对和 (ABS)
Absolute Sum模态组合法取结果的绝对值 (位移或内力) 对于每个振动模式并总结所有这些绝对值. 身体上, 它假设所有峰值模态响应同时发生. 通过这样做, 这是最保守的方法, 因为它使每个模态贡献都是积极的, 因此, 它在结构设计应用中并不流行. 总响应峰值的计算公式为:
\(r_o=\sum_{n=1}^{ñ} |r_{ñ,的}|\)
在哪里,
\(n\) 是个 \(^{日}\) 分析中考虑的振动模式
\(N\) 是分析中考虑的振动模式总数
\(r_o\) 是峰值总响应
\(r_{ñ,的}\) 是峰值模态响应 \(^{日}\) 振动模式
平方和的平方根 (SRSS)
The Square Root of Sum of the Squares 模态组合法对每个振动模态的结果的平方和取平方根, 提供对总响应峰值的估计. 这种模态组合方法为具有良好分离的固有频率的结构提供了出色的响应估计, 对于结构的固有频率没有很好分离的情况,不应使用此方法. 正式地, 峰值总响应可以表示如下:
\(r_o=\left(\和_{n=1}^{ñ} ^{2}_{ñ,的}\对)^{1/2}\)
在哪里,
\(n\) 是个 \(^{日}\) 分析中考虑的振动模式
\(N\) 是分析中考虑的振动模式总数
\(r_o\) 是峰值总响应
\(r_{ñ,的}\) 是峰值模态响应 \(^{日}\) 振动模式
完全二次组合 (质检总局)
完全二次组合法克服了 SRSS 在自然频率间隔很近的结构中组合模态响应时的局限性. 用这种方法, 峰值总响应是通过应用以下公式获得的:
\(r_o=\left(\和_{i = 1}^{ñ}\和_{n=1}^{ñ} \o{在} \cdot r_{IO} \cdot r_{不} \对)^{1/2}\)
在哪里,
\(ñ, \; i\) 是个 \(^{日}, \; 我^{日}\) 分析中考虑的振动模式
\(N\) 是分析中考虑的振动模式总数
\(r_o\) 是峰值总响应
\(r_{ñ,的}, \; r_{一世,的}\) 是峰值模态响应 \(^{日}, \; 我^{日}\) 振动模式
\(\o{在}\) 是在每个求和步骤中组合的两种模式的相关系数
上面的公式可以重写为两组独立的求和, 第一个与 SRSS 模态组合方法相同. 第二个双重求和包括所有交叉 (\(i \neq n\)) 条款, 其中每一个都可能是积极的或消极的, 这产生了这样一个事实,即使用 CQC 对峰值总响应的估计可能大于或小于 SRSS 提供的估计 :
\(r_o=\left( \和_{n=1}^{ñ} ^{2}_{ñ,的} + \底托{\和_{i = 1}^{ñ}\和_{n=1}^{ñ}}_{i \neq n} \o{在} \cdot r_{IO} \cdot r_{不} \对)^{1/2}\)
CQC 等式中只有一项未定义: 相关系数. 该系数最常用的方程之一是:
\(\o{在} = frac{\习^2(1+\钢底板设计欧洲规范{在})^ 2}{(1-\钢底板设计欧洲规范{在})^2+4\xi^2\beta_{在}}\)
在哪里,
\(\钢底板设计欧洲规范{在}\) 是自然频率之间的比率 \(我^{日}\) 和 \(^{日}\) 模式 (\(\omega_i / \omega_n\))
\(\习) 是结构的阻尼系数
参考资料
乔普拉, 一个. (2015, 六月 4). 结构动力学 (4特). 培生高等教育.
SkyCiv 结构 3D 新手? 今日免费注册!
产品开发人员
ng (民用)
领英



