Aperçu
La contrainte de flexion est l'une des valeurs les plus importantes dans la conception structurelle, comme pour la plupart des poutres horizontales, il s'agit généralement d'une conception critique ou déterminante. Comme une poutre horizontale est chargée, il génère moments de flexion contraintes dans les fibres supérieures et inférieures de la section qui peuvent surcharger la section, la faisant céder ou échouer complètement.
Lors du calcul de la contrainte de flexion, il est important de considérer ce qui suit:
- Moment d'inertie de votre section – affecte directement la contrainte de flexion
- Où sur la poutre vous vérifiez – la contrainte de flexion augmente généralement à mesure que vous vous éloignez de l'axe neutre de la section (d'où pourquoi les contraintes sont les plus importantes en haut et en bas de la section)
- Les propriétés du matériau – matériaux plus résistants (limite d'élasticité plus élevée par exemple) peut résister à des contraintes plus élevées et peut être plus adapté à certaines conceptions
- Formes de coupe transversale – comme avec le point (1) au dessus – différentes sections sont bien adaptées pour résister à des contraintes de flexion plus élevées, étant donné leurs valeurs de moment d'inertie plus élevées
- Direction de la contrainte – la flexion peut se produire à la fois dans le grand et le petit axe d'une section en fonction de la direction de la charge.
- Souvent, ces contraintes de flexion peuvent être combinées à des contraintes de cisaillement ou axiales (en raison de forces dans d'autres directions), augmenter la contrainte globale dans une poutre
Dans le guide suivant, nous explorerons principalement comment calculer la contrainte de flexion (en particulier dans un I Beam), mais il est important d'avoir le contexte ci-dessus à l'esprit lors de l'apprentissage de ces principes.
Comment calculer la contrainte de flexion dans les poutres?
Comprendre la contrainte de flexion est important car la flexion dans les poutres joue un rôle crucial dans la conception de celles-ci. Ce tutoriel examinera comment calculer la contrainte de flexion dans une poutre avec une formule. Cette formule lie la répartition des contraintes longitudinales dans une poutre aux moments de flexion agissant sur la section de la poutre. Nous supposons que le matériau de la poutre est linéaire-élastique (e.g. La loi de Hooke est applicable).
1. Calculer la contrainte de flexion à la main avec des formules de contrainte de flexion (Équations)
Prenons un exemple. Considérez la poutre en I illustré ci-dessous:
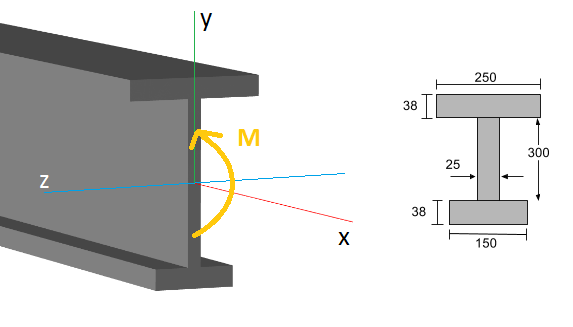
À tout point précis le long de la poutre (de l'axe des x), il existe un moment de flexion interne (M), normalement déterminé à l'aide d'un diagramme de moments fléchissants. La formule générale de la contrainte de flexion (ou stress normal) sur la section est:

Lorsque l'on considère une section spécifique de poutre, il devient clair que la contrainte en flexion atteindra sa valeur maximale à une distance spécifique de l'axe neutre (Y). C'est à dire, la contrainte de flexion maximale se produira soit à la fibre supérieure ou inférieure de la poutre , dépendant de quel distance est la plus grande:
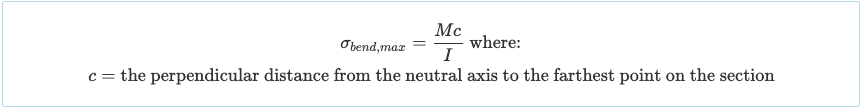
Considérons l'exemple réel de notre poutre en I montrée ci-dessus. Dans notre précédent tutoriel sur le moment d'inertie, nous avons déjà trouvé que le moment d'inertie autour de l'axe neutre est I = 4,74×108 mm4. Aussi, dans le tutoriel pour déterminer le centroïde, nous avons trouvé que le centre de gravité et donc l'emplacement de l'axe neutre est à 216.29 mm du bas de la section. Ceci est illustré ci-dessous:
Il est généralement utile de déterminer la contrainte de flexion maximale induite dans une section. Par exemple, supposons que nous avons déterminé, à partir du diagramme des moments fléchissants, que la poutre subit un moment fléchissant maximal de 50 kN-m ou 50,000 Nm (suite à la conversion des unités de mesure).
Nous devons ensuite déterminer si c'est la fibre supérieure ou inférieur de la section qui est la plus éloignée de l'axe neutre. Dans notre cas, la fibre inférieure est plus éloignée de l'axe neutre, et elle se trouve à c = 216.29 mm. Avec ces informations, nous pouvons procéder au calcul de la contrainte maximale en utilisant la formule de contrainte de flexion fournie ci-dessus:

De manière similaire, nous pouvons trouver la contrainte de flexion à la fibre supérieure, avec y = 159.71 mm de l'axe neutre (A.N.):

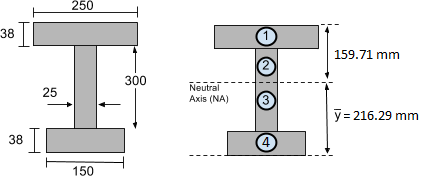
Finalement, nous devons déterminer si la contrainte axiale provoque une compression ou une tension des fibres de la section.
- Si la poutre s'affaisse comme un “U” vers le bas, les fibres supérieures subissent une compression (contrainte négative), tandis que les fibres inférieures subissent une tension (contrainte positive).
- Si la poutre s'affaisse à l'envers comme un “U” vers le bas, c'est la situation opposée: les fibres inférieures sont soumises à une compression, tandis que les fibres supérieures subissent une tension.
2. Calculer la contrainte de flexion à l'aide d'un logiciel
La section ci-dessus a discuté de la formule de contrainte de flexion pour le calcul manuel, mais vous n'avez plus besoin de le faire manuellement vous-même car Calculateur de poutres SkyCiv peut vous aider à trouver les contraintes de cisaillement et de flexion dans une poutre en un seul clic. En modélisant simplement la poutre, incorporant les appuis, et en appliquant des charges, vous pouvez obtenir les contraintes maximales à l'aide de ce calculateur de contrainte de flexion. L'image ci-dessous montre un exemple d'une poutre en I subissant une contrainte de flexion:
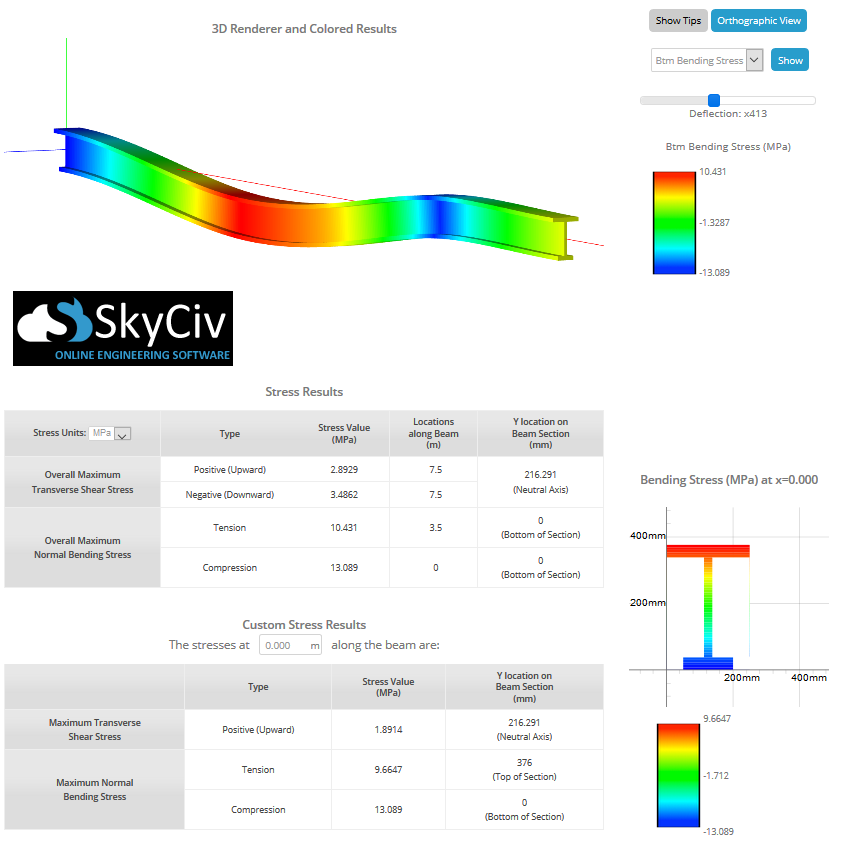
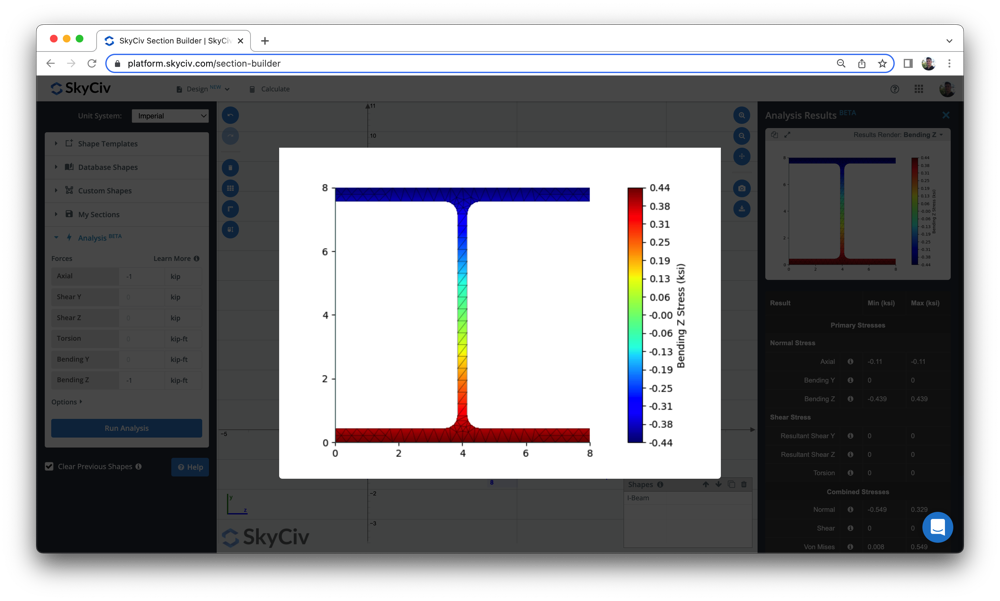
Les utilisateurs peuvent également utiliser le Créateur de sections pour calculer la contrainte de flexion et d'autres contraintes dans les sections de poutres, il s'agit simplement de construire et analyser votre section. N'hésitez pas à consulter notre outil pour calcul de poutres ci-dessus ou inscrivez-vous pour découvrir le nos autres offres logiciel gratuitement dès aujourd'hui!
Pour plus de documentations sur les poutres, visitez nos articles sur calculer la contrainte de flexion d'une section de poutre, comment trouver le moment de flexion, déterminer les réactions au support, et déviation du faisceau.


