Les principes fondamentaux du centre de gravité
Il est important de noter que sur une coupe transversale, dont la zone est uniforme partout, le centre de gravité peut être trouvé en prenant la somme des moments par rapport à un axe arbitrairement fixé, mais est généralement fixé à la fibre supérieure ou inférieure. Retrouvez notre précédent article sur le calcul du centre de gravité d'une section de poutre et calculateur de centroïde gratuit SkyCiv.
Fondamentalement, le centre de gravité peut être obtenu en prenant la somme des moments sur la somme de la zone. Ce qui s'exprime ainsi.
[math]
\bar{X}= frac{1}{A}\int xf gauche ( x droite )dx
[math]
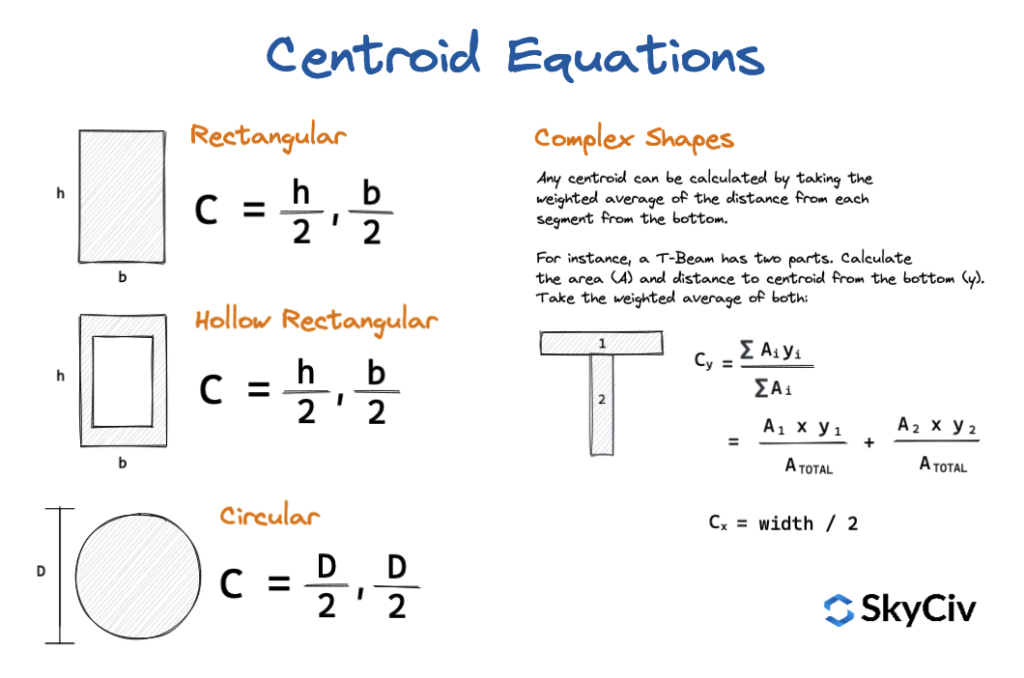
Résumé des équations centroïdes
Dans l'équation ci-dessus, F(X) est la fonction et x est le bras de moment. Pour mieux illustrer cela, nous dériverons le centre de gravité y d'un triangle arbitraire dont la base coïncide avec l'axe des x. Dans cette situation, la forme du triangle, que ce soit équilatéral, isocèle ou scalène n'est pas pertinent car tout est relatif uniquement à l'axe des x. Notez que la forme n’a pas d’importance si la base du triangle est coïncidente ou parallèle par rapport à l’axe. Ce ne sera pas le cas lors de la résolution du centroïde x. Au lieu, vous pouvez l'imaginer comme obtenant le centre de gravité de deux triangles rectangles par rapport à l'axe y. Pour des raisons pratiques, imaginons un triangle isocèle similaire au tableau de référence ci-dessous. Trouver la relation entre b et h donnera la relation suivante.
[math]
\frac{-Y}{X}= frac{-h}{b}
[math]
Notez que la pente est négative car nous imaginons que le triangle est droit. Si on imagine le triangle inversé, la pente serait positive. Indépendamment, la relation reste la même. Comme x = f(Y), la relation ci-dessus peut être réécrite comme suit.
[math]
x = f gauche ( y droit )= frac{b}{h}Y
[math]
Nous pouvons maintenant résoudre le centre de gravité. Ajustement de la première équation ci-dessus, nous obtenons ce qui suit.
[math]
\bar{Y}= frac{1}{A}\int yf left ( y droit )deux
[math]
Le fait de brancher des valeurs supplémentaires et de remplacer la relation ci-dessus donnera l'équation suivante.
[math]
\bar{Y}= frac{2}{bh}\int_{0}^{h} \frac{b}{h}et ^{2}deux
[math]
Simplifier,
[math]
\bar{Y}= frac{2}{h ^{2}}\la gauche [ \frac{et ^{3}}{3} \droite ]_{0}^{h}
[math]
[math]
\bar{Y}= frac{2}{h ^{2}}\la gauche [ \frac{h ^{3}}{3}-0 \droite ]
[math]
[math]
\bar{Y}= frac{2}{3}h
[math]
Notez que cette solution est prise par le haut. Le centre de gravité pris du bas doit alors être égal à 1/3 de h.
Formule pour les centroïdes de formes et de sections de poutre courantes
Vous trouverez ci-dessous une liste d'un variété de formes de section de poutre et la distance aux centres de gravité de la section. Les équations montrent comment trouver le centre de gravité d'une section particulière à partir de la base ou du point le plus à gauche de la section. Pour les abonnements SkyCiv Student et Structural, cette référence peut également être téléchargée sous forme de référence PDF à emporter partout avec vous. Les centroïdes d'une section de poutre sont extrêmement importants car ils localisent l'axe neutre et constituent l'une des premières étapes requises lors de l'analyse d'une section de poutre..
SkyCiv propose également un tableau récapitulatif complet des sections qui contient toutes les équations et formules relatives aux sections de poutre (moment d'inertie, zone etc.…).
L'équation pour divers centroïdes est répertoriée ci-dessous:
| RÉFÉRENCE | CY (Distance du bas) |
CX (Distance du point le plus à gauche) |
Centre de gravité des sections rectangulaires ou rectangulaires |
||
|---|---|---|
 |
[math] \dfrac{h}{2} [math] |
[math] \dfrac{b}{2} [math] |
Centre de gravité d'une section rectangulaire creuse |
||
 |
[math] \dfrac{b}{2} [math] |
[math] \dfrac{h}{2} [math] |
Centre de gravité d'un cercle ou d'une section circulaire |
||
 |
[math] \dfrac{D}{2} [math] |
[math] \dfrac{D}{2} [math] |
Équation du centre de gravité d'une section circulaire creuse |
||
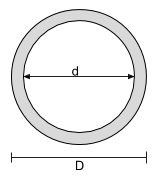 |
[math] \dfrac{D}{2} [math] |
[math] \dfrac{D}{2} [math] |
Centre de gravité d'un triangle isocèle |
||
 |
[math] \dfrac{h}{3} [math] |
[math] \dfrac{b}{2} [math] |
Centre de gravité d'une poutre en I |
||
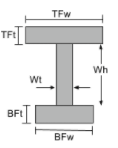 |
[math] \frac{TFw fois TFt fois gauche ( BFt + Wh + \frac{TFt}{2} \droite )}{TFw fois TFt + Wt fois Wh + BFw fois BFt} + [math] [math] \frac{Wt fois Wh fois gauche ( BFt + \frac{Wh}{2} \droite )}{TFw fois TFt + Wt fois Wh + BFw fois BFt} + [math] [math] \frac{BFw fois BFt fois gauche ( \frac{BFt}{2} \droite )}{TFw fois TFt + Wt fois Wh + BFw fois BFt} [math] |
[math] TFw > BFw, \frac{TFw}{2}[math] [math] BFw > TFw, \frac{BFw}{2} [math] |
Centre de gravité d'une section en T |
||
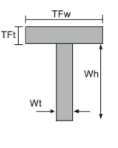 |
[math] \frac{Wt fois Wh fois gauche ( \frac{Wh}{2} \droite )}{TFw fois TFt + Wt fois Wh } + [math] [math] \frac{TFw fois TFt fois gauche ( Wh + \frac{TFt}{2} \droite ) }{TFw fois TFt + Wt fois Wh } [math] |
[math] \frac{TFw}{2} [math] |
Centre de gravité d'une section en C |
||
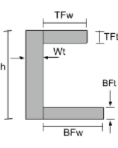 |
[math] \frac{TFw fois TFt fois gauche ( h – \frac{TFt}{2} \droite )}{TFw fois TFt + Wt fois Wh + BFw fois BFt} + [math] [math] \frac{Wt fois h fois gauche ( \frac{h}{2} \droite )}{TFw fois TFt + Wt fois Wh + BFw fois BFt} + [math] [math] \frac{BFw fois BFt fois gauche ( \frac{BFt}{2} \droite )}{TFw fois TFt + Wt fois Wh + BFw fois BFt} [math] |
[math] \frac{TFt fois TFw fois gauche ( Poids + \frac{TFw}{2} \droite )}{TFt fois TFw + h fois Wt + BFt fois BFw} + [math] [math] \frac{h fois Wt fois gauche ( \frac{Poids}{2} \droite )}{TFt fois TFw + h fois Wt + BFt fois BFw} + [math] [math] \frac{BFt fois BFw fois gauche ( Poids + \frac{BFw}{2} \droite )}{TFt fois TFw + h fois Wt + BFt fois BFw} [math] |
Centroïde d'un Angles |
||
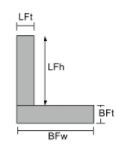 |
[math] \frac{LFt fois LFh fois gauche ( BFt + \frac{LFh}{2} \droite ) }{LFt fois LFh + BFw fois BFt} + [math] [math] \frac{BFw fois BFt fois gauche ( \frac{BFt}{2} \droite )}{LFt fois LFh + BFw fois BFt} [math] |
[math] \frac{LFh fois LFt fois gauche ( \frac{LFt}{2} \droite )}{LFh fois LFt + BFt fois BFw} + [math] [math] \frac{BFt fois BFw fois gauche ( \frac{BFw}{2} \droite )}{LFh fois LFt + BFt fois BFw} [math] |
Équations automatiques pour le centroïde du faisceau
Consultez nos Calculateur de centroïde gratuit, une version simplifiée de Générateur de sections SkyCiv, pour calculer automatiquement le centroïde du faisceau sans avoir besoin de calculs manuels. Ou inscrivez-vous aujourd'hui pour commencer!

