Table des matières

• Aperçu – Quel est le moment d'inertie
• Exemple – Comment calculer le moment d'inertie
• Formule et équations
• Calculatrices
• Questions pratiques

Aperçu – Quel est le moment d'inertie?

Dans le cadre de l'ingénierie des structures, le moment d'inertie est une propriété de section utilisée pour déterminer la capacité d'un élément structurel à résister aux forces de flexion et de torsion. C’est généralement un assez bon indicateur de la rigidité et de la résistance des sections sous charge.. Un moment d'inertie plus élevé signifie que la structure est mieux équipée pour résister à la flexion et à la déflexion, ce qui en fait un facteur essentiel dans la conception des poutres, Colonnes, et autres composants porteurs. À noter: Parfois, cela est défini à tort comme le deuxième moment de inertie, cela est fautif. Les autres noms du moment d’inertie sont: moment d'inertie de l'aire, ou deuxième moment de Région.

Exemple – Comment calculer le moment d'inertie d'une section de poutre

Avant de trouver le moment d'inertie d'une section de poutre (également connu sous le nom de deuxième moment d'aire ou moment quadratique), son centroïde (ou centre de gravité) doit être connu. Par exemple, si le moment d'inertie de la section autour de son axe horizontal (XX) l'axe est voulu, la distance verticale (Y) du centre de gravité est d'abbord requise (Veuillez consulter nos tutoriels sur le calcul du centre de gravité d'une section de poutre et calcul du moment statique/premier moment de l'aire).

Avant de débuter, si vous cherchez notre Calculateur de moment d'inertie gratuit appuyez sur le lien précédent. Cet outil calcule le centre de gravité, moment d'inertie, et d'autres résultats, tout en vous montrant les calculs étape par étape! Sinon, regardons étape par étape un exemple de calcul du moment d'inertie:

Étape 1: Segmentez la section de poutre en plusieurs parties

Lors du calcul du moment d'inertie, il faut calculer le moment d'inertie de chaque petit segment individuel. Commençons par diviser la section en plus petites sections rectangulaires. Par exemple, considérez la section de poutre en I ci-dessous, qui a également été présenté dans notre turotiel de calcul de centroïde. Divisions cette section en 3 segments rectangulaires:

 

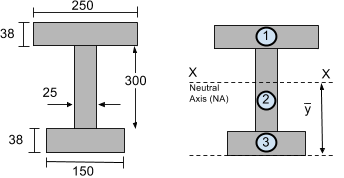
Étape 2: Calculer l'axe neutre (A.N.)

L'axe neutre (A.N.) ou l'axe horizontal XX est situé au centroïde ou au centre de gravité de la section. Dans notre tutoriel sur le calcul du centroïde, le centre de gravité de cette section a été trouvé comme étant à 216.29 mm du bas de la section – voir comment trouver le centre de gravité d'une forme (tutoriel). Alternativement, vous pouvez également simplement calculer le centre de gravité à partir de notre Calculatrice de centroïde ou des Équations pour déterminer le centroïde d'une section.

Le calcul du centre de gravité, ou axe neutre, est essentiel dans comment calculer le moment d'inertie d'une poutre, car c'est l'axe autour duquel agit le moment d'inertie.

Étape 3: Calculer le Moment d'Inertie

Pour calculer le moment d'inertie total de la section, nous devons utiliser le “Théorème des axes parallèles”:

Étant donné que nous avons divisé notre section en trois parties rectangulaires, il faut calculer le moment d'inertie de chacune de ces sections. Il est bien connu que l'équation du moment d'inertie d'un rectangle autour de son axe centroïde est simplement:

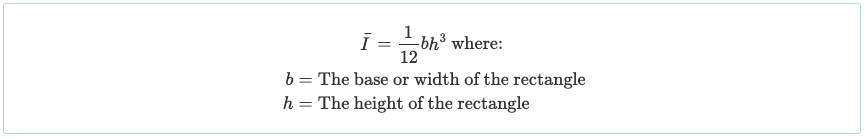
Le moment d'inertie des autres formes est souvent indiqué au début ou à la fin des manuels d'ingénierie, sinon dans le guide suivant: moment d'inertie des formes. Cependant, la forme rectangulaire est très courante pour les sections de poutre, il est donc probablement utile de mémoriser sa formule.

Nous avons maintenant toutes les informations nécessaires pour utiliser le “Théorème des axes parallèles” et trouver le moment d'inertie total de la section de notre poutre en I. Dans notre exemple de moment d'inertie est calculé comme suit:

Voilà donc comment calculer le moment d'inertie pour les sections de poutre. Ce résultat est critique en ingénierie des structures et est un paramètre important dans la détermination de la déflexion d'une poutre. Nous espérons que vous avez apprécié le tutoriel et attendons avec impatience vos commentaires. Pour plus d'informations, visitez notre tutoriel sur Formule et équations du moment d'inertie.

Formule et équations

Chaque type de section (rectangulaire, Je rayonne, Circulaire) a sa propre formule pour un calcul rapide. Ce sont des équations simplifiées qui permettent aux ingénieurs de calculer rapidement et facilement cette propriété importante..

Les équations sont une expression simplifiée des étapes ci-dessus. Par exemple, la formule du moment d'inertie d'un rectangle creux est essentiellement le MOI de la plus grande section – le plus petit (interne) section:

[math] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [math]

SkyCiv a mis en place une ressource pratique pour les Formule du moment d'inertie.

Calculatrices

Tel que discuté précédemment, il existe plusieurs façons de calculer le moment d'inertie, dont l'utilisation d'un logiciel pour faciliter le processus.

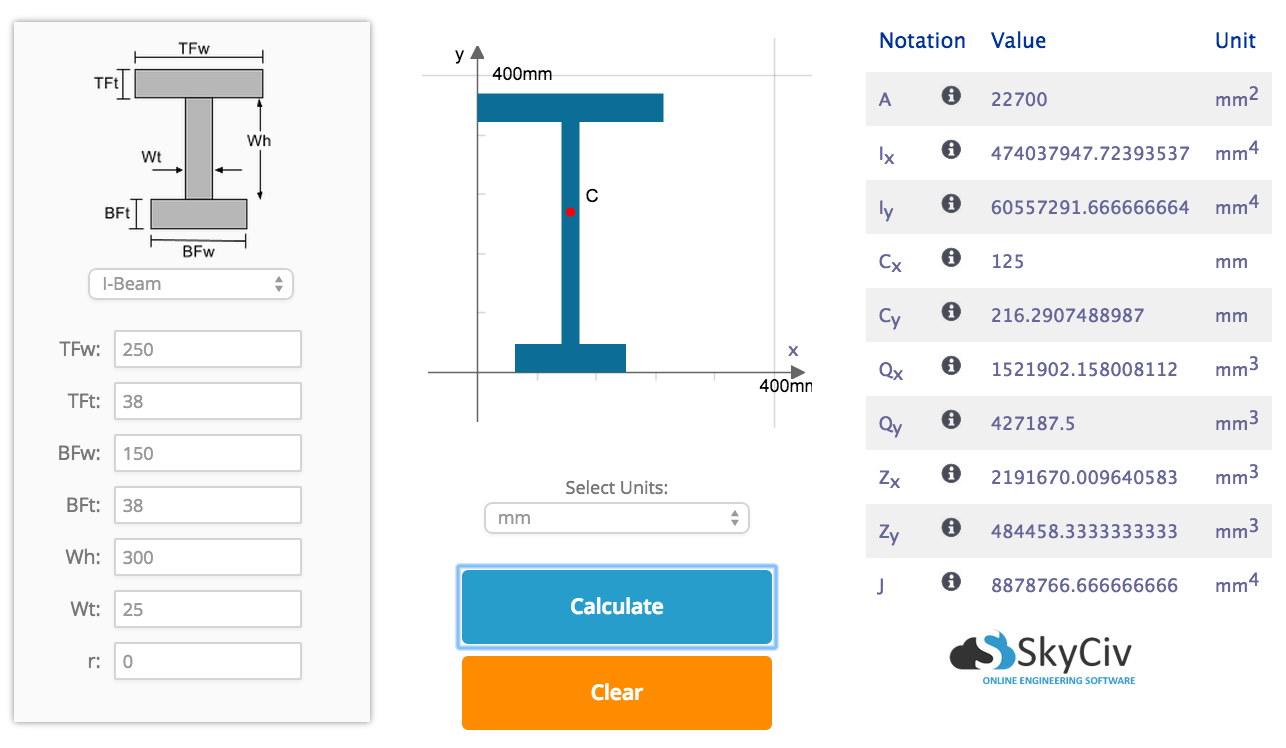
Générateur de sections SkyCiv est un outil de conception de sections entièrement performant qui va bien au-delà du calculateur de moment d'inertie. Il vous montrera également les calculs étape par étape pour trouver le moment d'inertie.:

Aussi, vous pouvez utiliser les résultats de notre Calculateur de moment d'inertie gratuit pour vérifier votre travail. Cela calculera toutes les propriétés de votre section transversale et constitue une référence utile pour calculer le centre de gravité, l'aire, et le moment d'inertie de vos sections de poutre! L'avantage supplémentaire est que vous pouvez également inclure le rayon dans les coins, pour des calculs plus précis.

Inscrivez-vous aujourd'hui pour en savoir plus sur le logiciel SkyCiv, ou réserver une DEMO GRATUITE pour vous faire assister dans vos projets d'ingénierie (pour les utilisateurs existants)!

Aussi, SkyCiv a un gratuit Calculateur de propriétés de section dans le cadre de la bibliothèque Quick Design. C'est un outil simplifié, mais calculera également le moment d'inertie des formes de section courantes.

Inscrivez-vous aujourd'hui

Questions pratiques

Question 1: Coupe rectangulaire

Problème: Calculer le moment d'inertie (Ixx et Iyy) pour une section rectangulaire d'une largeur (b) de 200 mm et une hauteur (h) de 300 mm.

Solution: Les formules du moment d'inertie d'un rectangle sont:

[math] \dfrac{bh ^ 3}{12} [math]​

Remplacement des valeurs données:

• b=200 mm
• h=300 mm

Pour Ixx:

[math] \dfrac{bh ^ 3}{12} = dfrac{200(300^ 3)}{12} = 450×10^6 mm^4 ​ [math]​

Pour Iyy:

[math] \dfrac{bh ^ 3}{12} = dfrac{300(200^ 3)}{12} = 200×10^6 mm^4 ​ [math]​

Question 2: Poutre en I

Problème: Calculer le moment d'inertie du grand axe (Ixx) d'une section de poutre en I avec les dimensions suivantes:

• Largeur de la bride supérieure (TFw) = 6 in
• Épaisseur de la bride supérieure (TFt) = 0.43 in
• Profondeur de section = 6 in
• Épaisseur de l'âme (Poids) = 0.29 in
• Largeur de la bride inférieure (BFw) = 6 in
• Épaisseur de la bride inférieure (BFt) = 0.43 in

Solution:

[math] JE_{xx} = 82.8 dans ^4​ [math]​