Comment calculer les forces axiales d'un système de fermes à l'aide de la méthode des joints?
Dans ce tutoriel, nous expliquerons comment utiliser la méthode des joints pour calculer les efforts internes des éléments dans un système ou une structure en treillis.
Ces forces sont appelées forces axiales et sont très importantes dans l'analyse des fermes. Si vous ne savez pas ce qu'une ferme est vue dans notre article – Qu'est-ce qu'un treillis. La méthode des joints consiste essentiellement à examiner chacun des «joints»’ (où les membres se rencontrent) et appliquer des équations statiques pour résoudre.
La grande chose est, SkyCiv Truss le fait automatiquement pour vous. Modélisez vos propres fermes et le logiciel montrera de manière interactive, étape par étape, la méthode des joints!

Étape 1: Calculer les réactions aux supports
Première, on calcule le réactions aux appuis. Nous allons commencer par regarder un exemple simple de 5 système de poutre de membre:
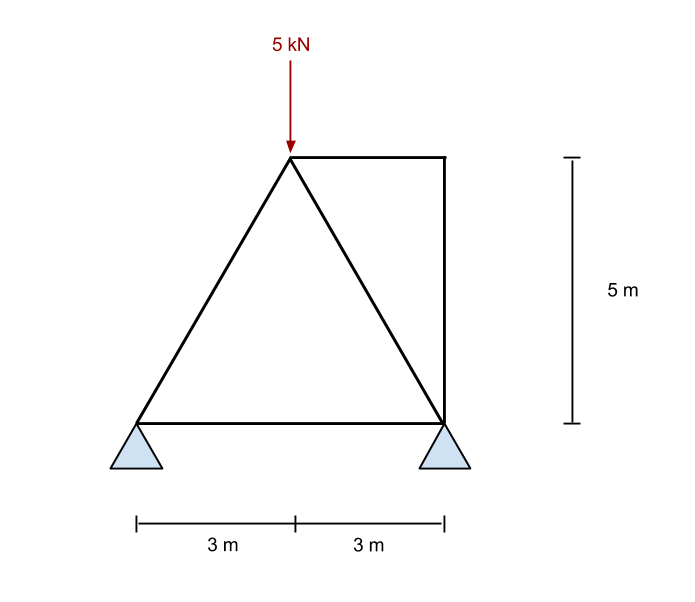
Pour calculer le moments de flexion dans ce système de treillis, on prend d'abord la somme des moments de la réaction de gauche égale à zéro. Nous faisons cela en ignorant tous les membres et en regardant simplement les forces et les appuis dans la structure. C'est la même que la méthode utilisée dans les réactions de moment de flexion dans notre tutoriel précédent.
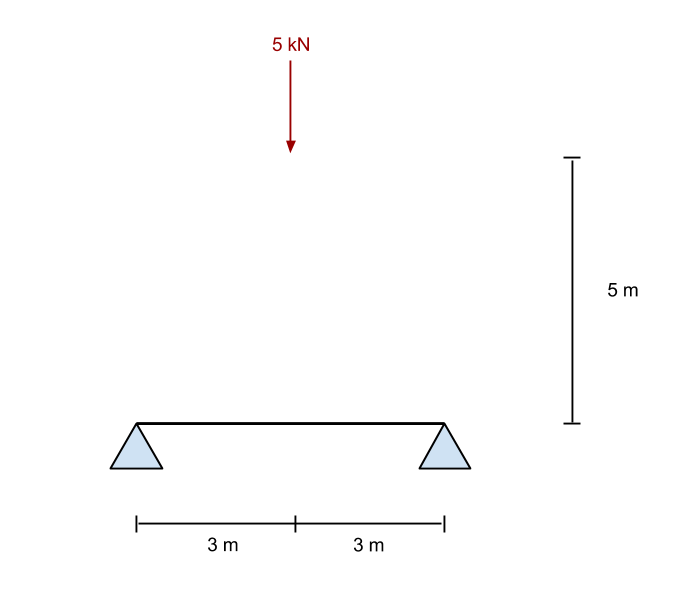
À partir des équations ci-dessus, nous résolvons la force de réaction au point B (le bon support). Dans notre exemple, cela fonctionne pour être 2.5 kN vers le haut. Maintenant, si on prend la somme des forces dans le y (vertical) direction, on trouve que le support A (le support gauche) est également donné comme 2.5 kN.
Étape 2: Considérez l'un des supports:
Maintenant que nous avons les forces de réaction, nous pouvons commencer l'analyse du reste de cette structure en treillis. Tout d'abord, nous nous tournons vers l'une de nos forces connues – dans ce cas, nous considérerons la réaction de support gauche de +2.5 kN. Puisque nous savons que cette force se produit à ce stade, nous considérerons juste ce point isolément. Nous répétons ce processus plusieurs fois, il est donc important de pratiquer et d'apprendre le processus afin d'avoir une bonne compréhension de la résolution des forces axiales dans les structures en treillis. Donc encore, considérez le premier point au support:
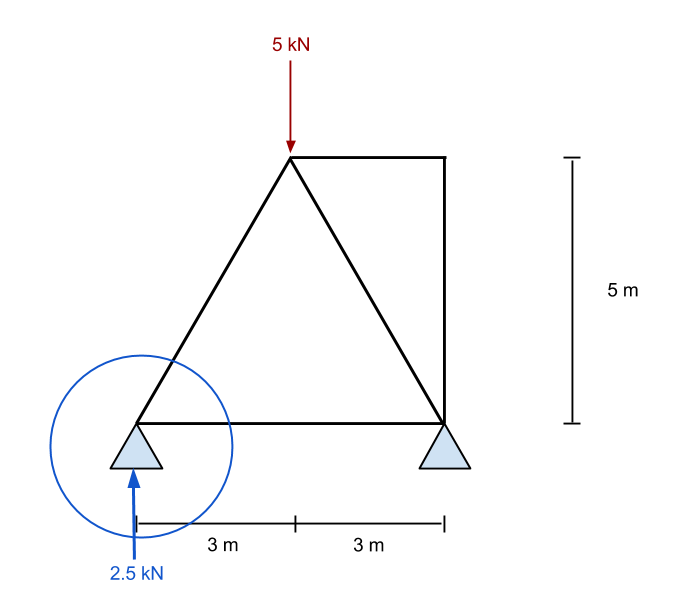
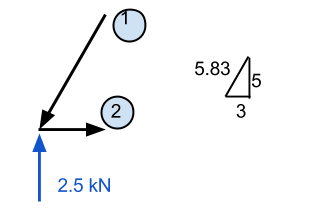
Zoomer sur ce point, on voit toutes les forces connues agir sur ce point. De la statique, nous savons que les forces dans les directions x et y doivent être égales à zéro. En conséquence, si on sait qu'il y a une force verticale ascendante, alors il doit y avoir une force descendante pour le contrer. Puisque nous avons déjà la valeur d'une force tournée vers le haut, alors nous essaierons d'évaluer le numéro de membre 1 première.
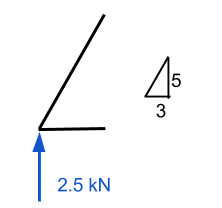
Ici, nous avons besoin de quelques connaissances sur les vecteurs. Il est important de se rappeler que toutes les forces doivent être égales à zéro pour les directions x et y. Dans notre exemple, la distance horizontale est de 3 m tandis que la verticale est de 5 m – nous laissant avec l'hypoténuse égale à environ 5.83 m. Utiliser ceci, on peut en déduire que la composante de force normale du membre 1 est égal à (5.83)/(5) fois la force verticale de 2.5 kN. Cela équivaut à 2.92 kN et DOIT être une force agissant vers le bas si le point doit rester stationnaire.
Membre 2 peut être calculé de la même manière. Si nous connaissons ce membre 1 agit à la baisse, alors on sait qu'il faut aussi agir à gauche. En conséquence, nous connaissons le membre 2 doit générer une force qui tire le point vers la droite pour maintenir les forces dans la direction x. Cette valeur est calculée par (3/5.83) X 2.92 kN et est égal à 1.51 kN.
Étape 3: Passer à un autre point:
Après avoir calculé les efforts internes du premier membre de notre ferme, nous allons maintenant examiner un autre point pour répéter le processus:
Encore une fois, nous allons zoomer sur le point de référence et considérer toutes les forces connues agissant sur le point:
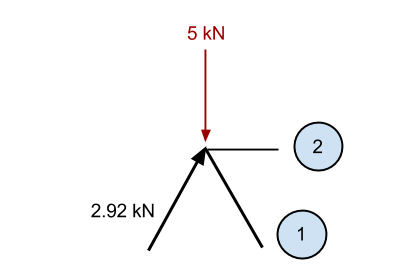
Un peu de la même manière qu'avant, si nous additionnons la composante verticale connue du 2.92 membre kN (2.5 kN dans le sens vertical) et la – 5kN force vers le bas, alors nous avons un excès dans le sens descendant de 2.5 kN (5 – 2.5). En conséquence, nous connaissons ce membre 1 doit provoquer une force vers le haut pour maintenir le point statique. Cette force doit avoir une composante verticale de 2.5 kN, et comme il est au même angle que le membre précédent, alors la force axiale interne doit également être 2.92 kN.
Maintenant, nous considérons les forces dans la direction x. À ce point, toute la force verticale du membre 1 résiste à la force verticale de l'élément précédemment calculé. Cela signifie que la somme des forces dans la direction x est déjà nulle. En conséquence, il ne peut y avoir aucune force dans Member 2 ou bien le point deviendra déséquilibré et ne sera plus statique.
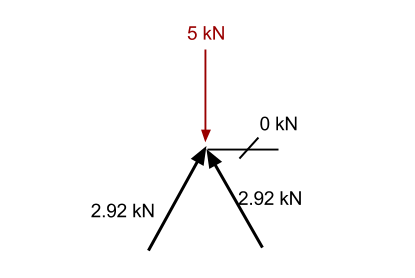
Étape 4: Passer à un autre point:
En regardant ce point, on voit qu'il y a un cas particulier. Dans cette situation, toute force poussant vers le haut n'aura aucune action de résistance possible, car il n'y a aucun autre élément capable de fournir une force vers le bas pour maintenir le point statique. En conséquence, puisque la somme des forces doit être nulle, ce membre ne peut avoir aucune force associée. Il, donc, n'a aucune force et est connu comme un membre zéro.
Encore une fois, si nous regardons la somme des forces dans la direction x, nous pouvons voir qu'il n'y a qu'un seul membre qui a une force dans la direction x. En conséquence, cela doit aussi avoir 0 force axiale pour que la somme des forces soit égale à zéro.

Solution finale
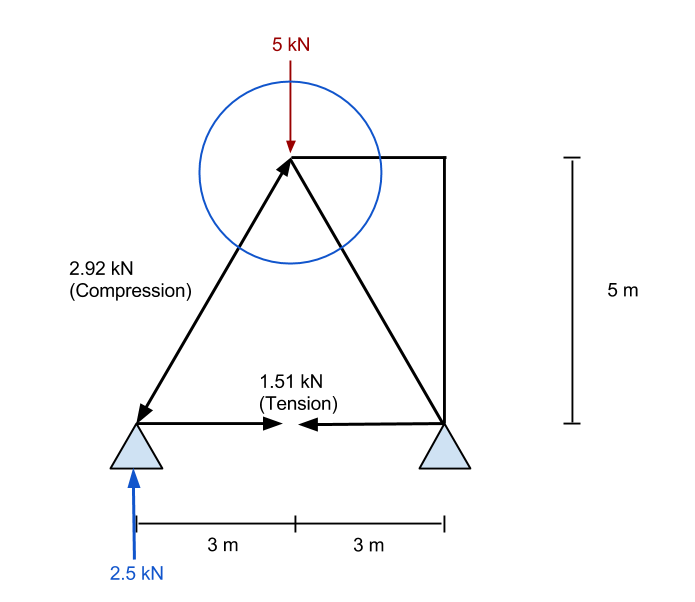
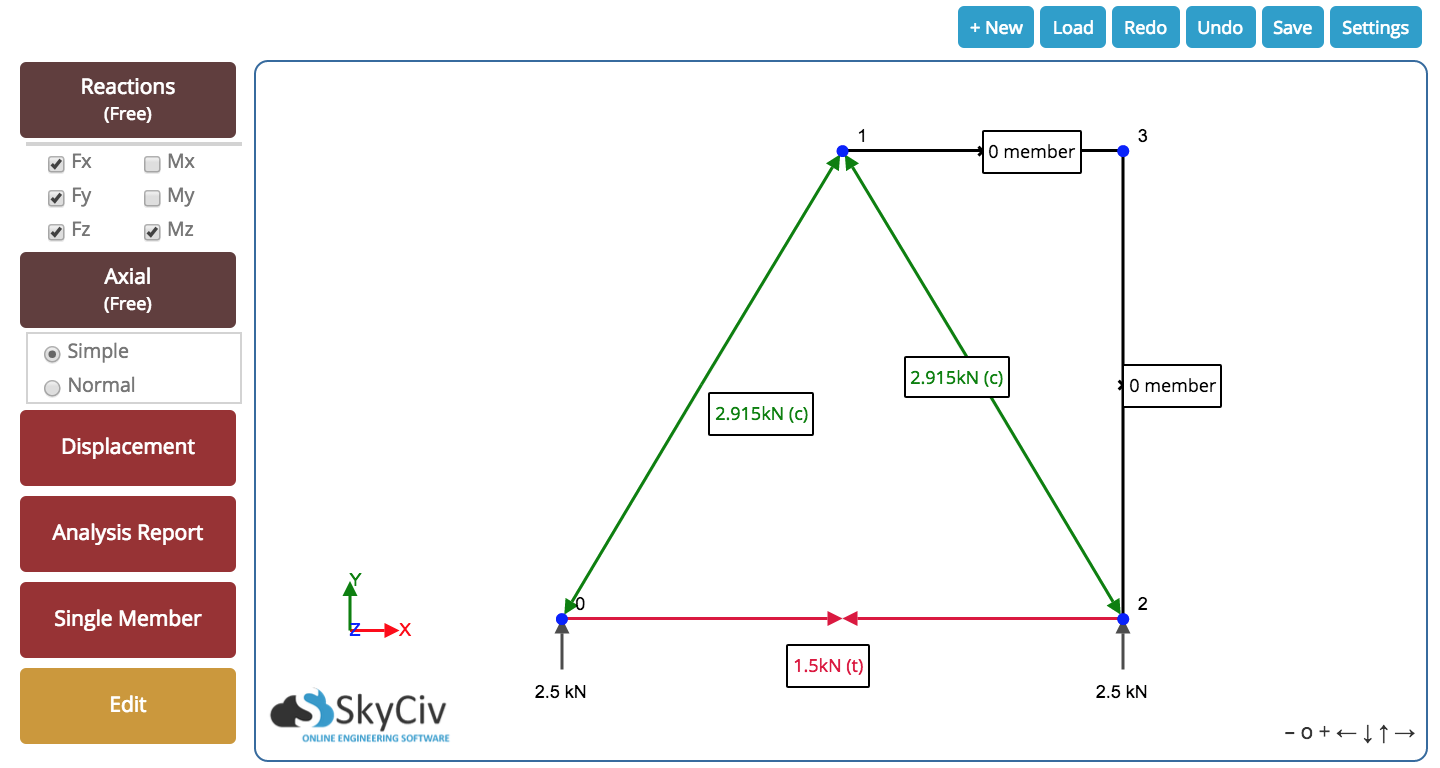
Ensuite, nous nous retrouvons avec le résultat suivant pour notre ferme. Nous pouvons voir toutes les forces axiales résultantes à l'intérieur de l'élément et le réactions aux appuis. Le résultat suivant est tiré de notre Calculatrice de fermes gratuite – Essayez, c'est gratuit!
Étapes simples
- Commencez toujours par calculer les réactions aux supports
- Choisissez un point avec une force connue et regardez-le isolément
- Utiliser la géométrie vectorielle et la somme des forces = 0 pour résoudre les autres forces membres
- Répétez le processus jusqu'à ce que tous les membres soient résolus
- N'oubliez pas de rechercher les membres zéro
Tutoriel pertinent
- Résolution d'un treillis par la méthode des sections. Comprend une vidéo et un guide étape par étape
SkyCiv Truss
SkyCiv Truss peut calculer automatiquement la méthode des articulations pour vous. Ou essayez notre Calculatrice de fermes gratuite qui vous donnera la réponse finale (aucun calcul manuel).
Pour explorer plus de fonctionnalités du logiciel SkyCiv, inscrivez-vous aujourd'hui pour commencer!


