Table des matières

• Calcul du diagramme des moments fléchissants
• Calculer le diagramme des moments fléchissants à la main
• Convention de signe pour les diagrammes de moments fléchissants
• Comment calculer la flexion à l'aide de SkyCiv Beam

Calcul du diagramme des moments fléchissants

Vous trouverez ci-dessous des instructions simples sur la façon de calculer le diagramme du moment de flexion d'un poutre simplement appuyée. Cette méthode vaut la peine d'être apprise, car elle est très polyvalente (et peut être adapté à de nombreux problèmes différents). Le calcule du moment fléchissant d'une poutre est une pratique très courante pour les ingénieurs en structure et revient souvent dans les examens du collège et du lycée. En passant, le logiciel SkyCiv Beam peut afficher ces calculs manuels automatiquement avec tout calcul de poutre! Nous comparerons d'ailleurs le tutoriel d'aujourd'hui avec un exemple tiré directement du module de calcul manuel dans SkyCiv Beam.

Tout d'abord, qu'est-ce qu'un moment de flexion.? Un moment est une force de rotation qui se produit lorsqu'une force est appliquée perpendiculairement à un point à une distance donnée de ce point. Il est calculé comme la force perpendiculaire multipliée par la distance entre la force et le point. Un moment de flexion est simplement la flexion qui se produit dans une poutre en raison d'un moment.

Il est important de se souvenir de deux choses lors du calcul des moments de flexion; (1) les unités standard sont le Nm et (2) lorsque la fibre supérieure est comprimée, la flexion est considérée comme positive. Maintenant que les choses sont bien définies, passons aux étapes pour calculer un diagramme de moment fléchissants!

Calculateur de poutre gratuit

Calculer le diagramme des moments fléchissants à la main

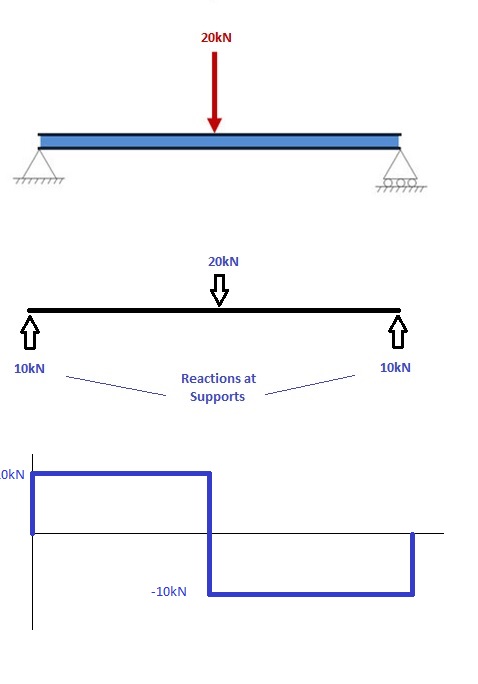
1. Calculer les réactions aux appuis et dessiner un diagramme de corps libre (DCL)

Si vous ne savez pas comment déterminer les réactions aux appuis – accèdez au tutoriel précédent. Une fois que vous avez déterminé les réactions d'appui, dessinez votre diagramme de corps libre ainsi que le diagramme d'efforts tranchants sous la poutre. Ensuite, le calcul des moments peut être effectué par la suite:

2. De gauche à droite, faire “coupes” avant et après chaque réaction ou charge

Pour calculer le moment de flexion d'une poutre, nous devons travailler de la même manière que nous l'avons fait pour le diagramme des efforts tranchants. À partir de x = 0 nous allons nous déplacer au long de la poutre et calculer le moment de flexion à chaque point de coupe.

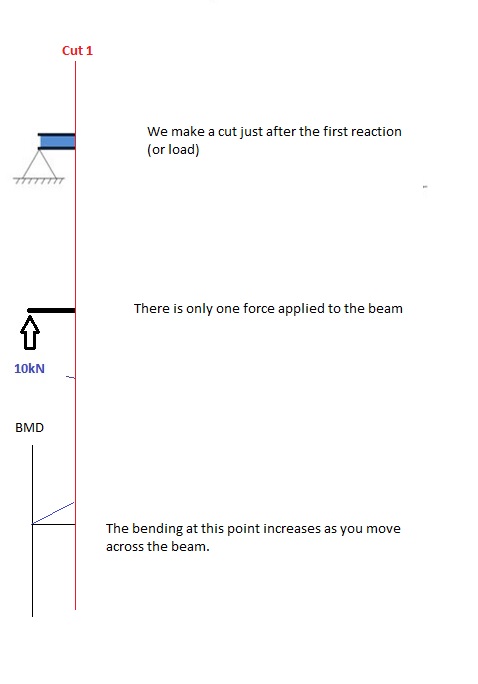
Coupe 1

Faire une “Coupe” juste après la première réaction d'appui de la poutre. Dans notre exemple simple:

Donc, la poutre est coupée, nous ne considérons que les forces appliquées à gauche de notre coupe. Dans le cas présent, nous avons une force de 10 kN vers le haut situé à l'appui. Souvenez-vous, un moment de flexion est simplement la force multiplié par la distance. À mesure que nous nous éloignons de la force, l'amplitude du moment de flexion augmentera. Nous pouvons le voir dans notre DMF. L'équation de cette partie de notre diagramme des moments fléchissants est donc de:

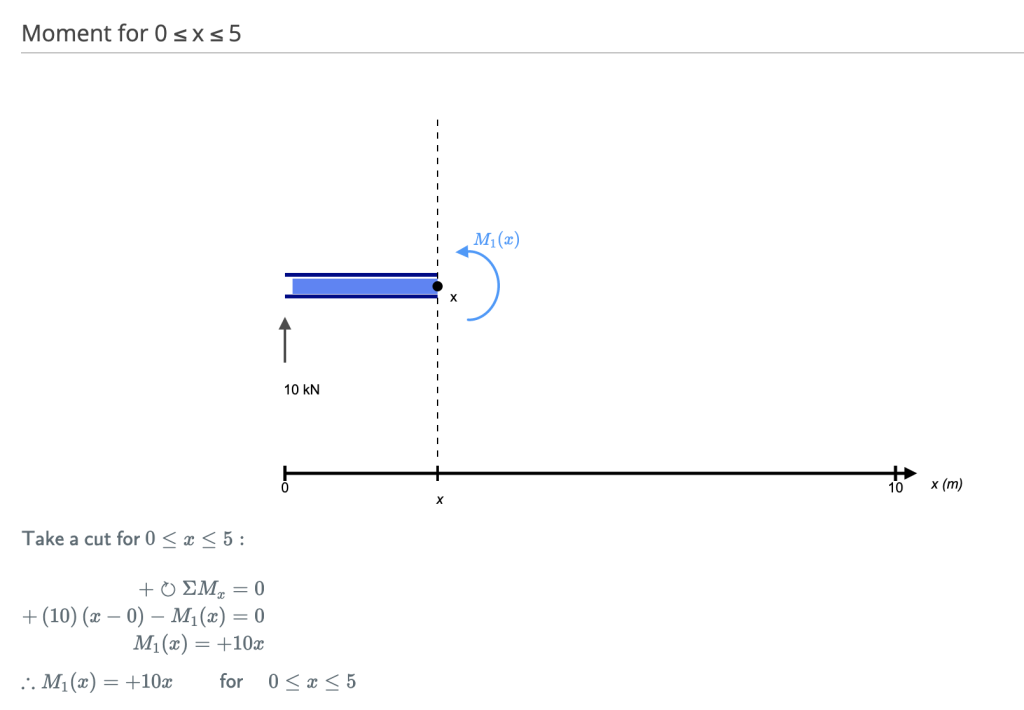
[Source: SkyCiv Calcul à la main du module de calcul de poutres]

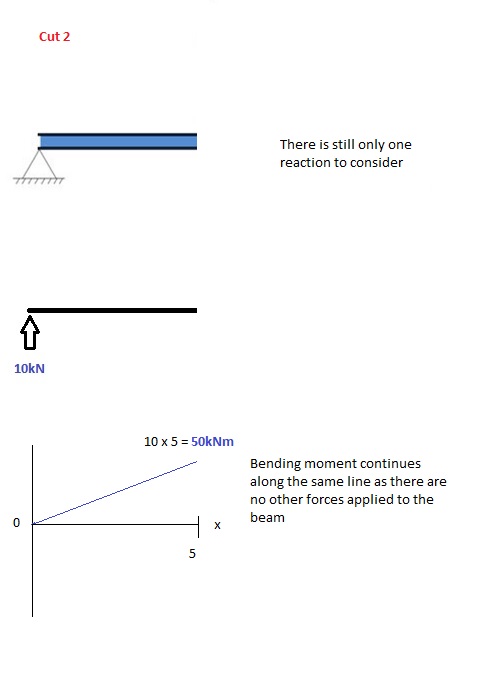
Coupe 2

Cette coupe est faite juste avant la deuxième force le long de la poutre. Puisqu'il n'y a pas d'autres charges appliquées entre la première et la deuxième coupe, l' équation du moment de flexion restera le même. Cela signifie que nous pouvons calculer le moment de flexion maximal (dans ce cas au milieu, ou x = 5) en remplaçant simplement x = 5 dans l'équation ci-dessus:

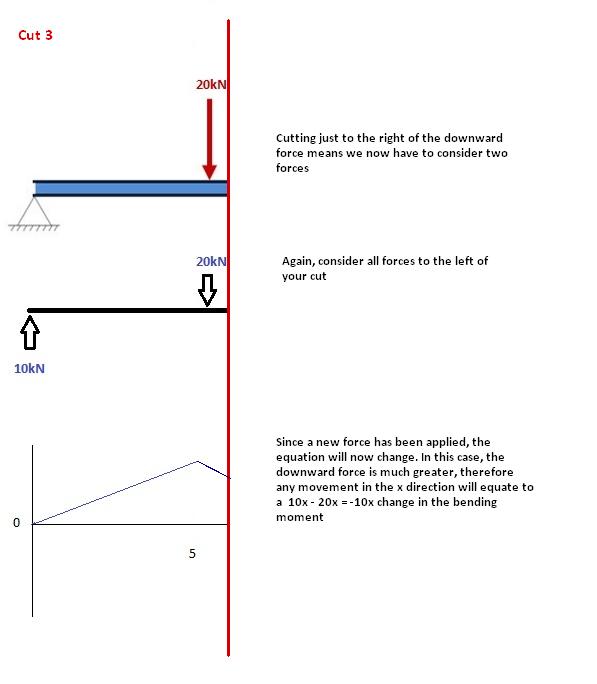
Coupe 3

Cette coupe est faite juste après la deuxième force le long de la poutre. Maintenant, nous avons DEUX forces qui agissent à gauche de notre coupe: une réaction d'appui de 10 kN vers le haut et une charge de 20 kN vers le bas. Nous devons donc considérer ces deux forces au fur et à mesure que nous progressons le long de notre poutre. Pour chaque mètre, lorsque nous nous déplaçons au long de la poutre, il y aura un moment +10kNm ajouté dû à la première force et un moment de -20kNm dû à la seconde.

Donc après le point x = 5, notre équation du moment de flexion devient: M(X) = 50 +10(x-5) – 20(x-5) M(X) = 50 -10(x-5) pour 5 ≤ x ≤ 10 REMARQUE: La raison pour laquelle nous écrivons (x-5) est parce que nous voulons connaître la distance au point x = 5 seulement. Tout ce qui précède ce point est représenté par l'équation précédente.[Source: SkyCiv Calcul à la main du module de calcul de poutres]

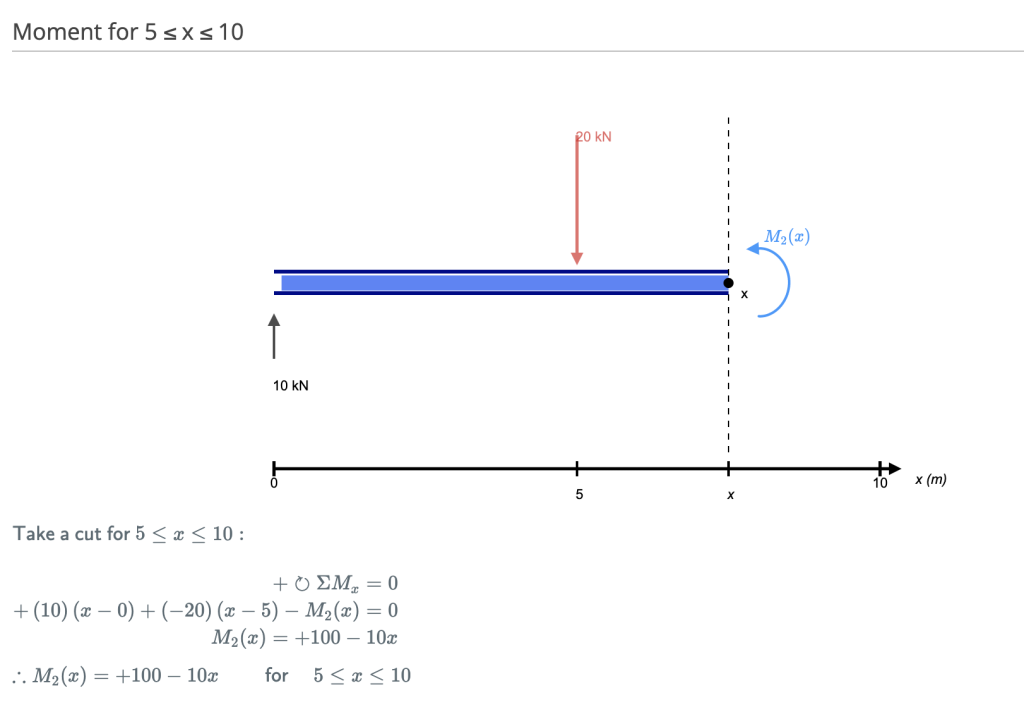
Coupe 4

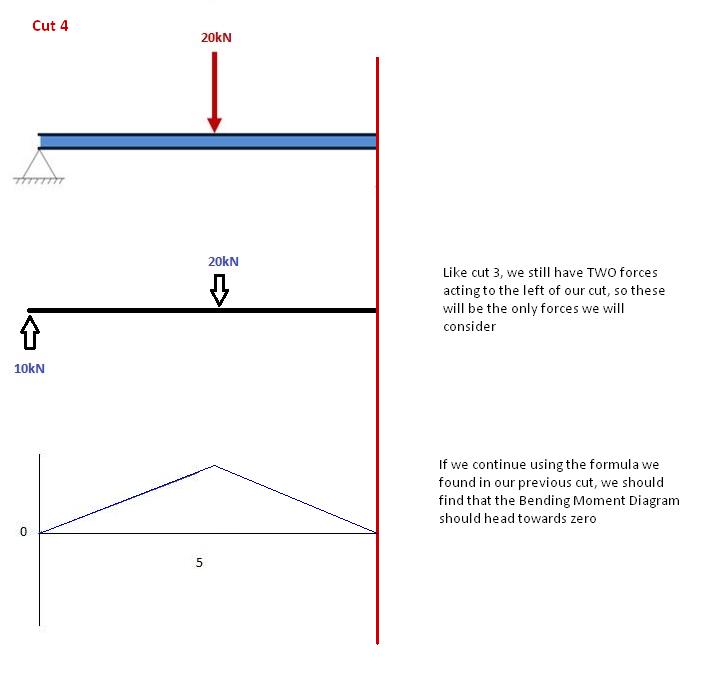
Encore une fois, continuons vers la droite de notre poutre et faisons une coupe juste avant notre prochaine force. Dans le cas présent, notre prochaine coupe aura lieu juste avant la réaction de l'appui droit. Puisqu'il n'y a pas d'autres forces entre le support et notre coupe précédente, l'équation demeure la même: M(X) = 50 -10(x-5) pour 5 ≤ x≤ 10 . Substituons x = 10 dans cette formule pour trouver le moment de flexion à la fin de la poutre: M(X) = 50 – 10(10-5) = 0kNm. Ceci est parfaitement logique. Puisque notre poutre est statique (et sans rotation aux appuis) il est logique que notre poutre ait un moment nul à ce point lorsque nous considérons toutes nos forces. Il satisfait également l'une de nos conditions initiales, que la somme des moments à l'appui soit égale à zéro. REMARQUE: Si vos calculs vous donnent un nombre autre que 0, c'est un bon indice qu'il y a une erreur dans les calculs!

Le résultat final, comme affiché dans SkyCiv Beam:

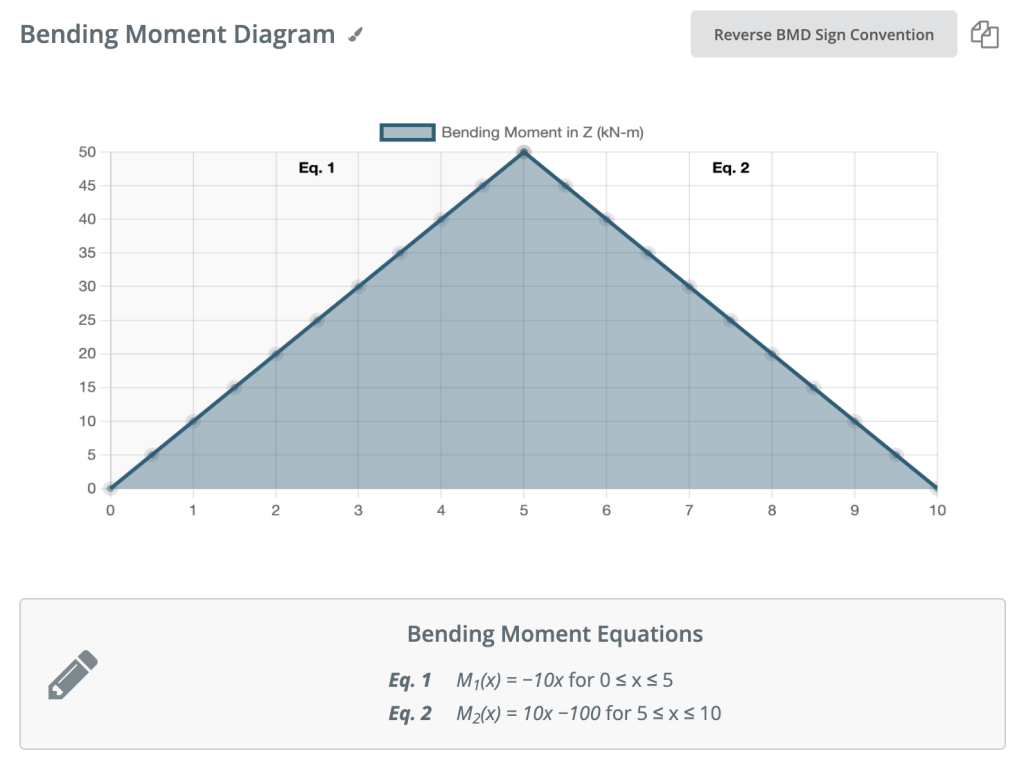
Convention de signe pour les diagrammes de moments fléchissants

Nous avons expliqué ci-dessus comment trouver le moment de flexion. Les diagrammes des moments de flexion peuvent devenir quelque peu déroutants en ce qui concerne les conventions de signe. Vous pouvez voir le même schéma dessiné dans des directions opposées en fonction de la source. La convention de signe utilisée par SkyCiv est affichée ci-dessous.

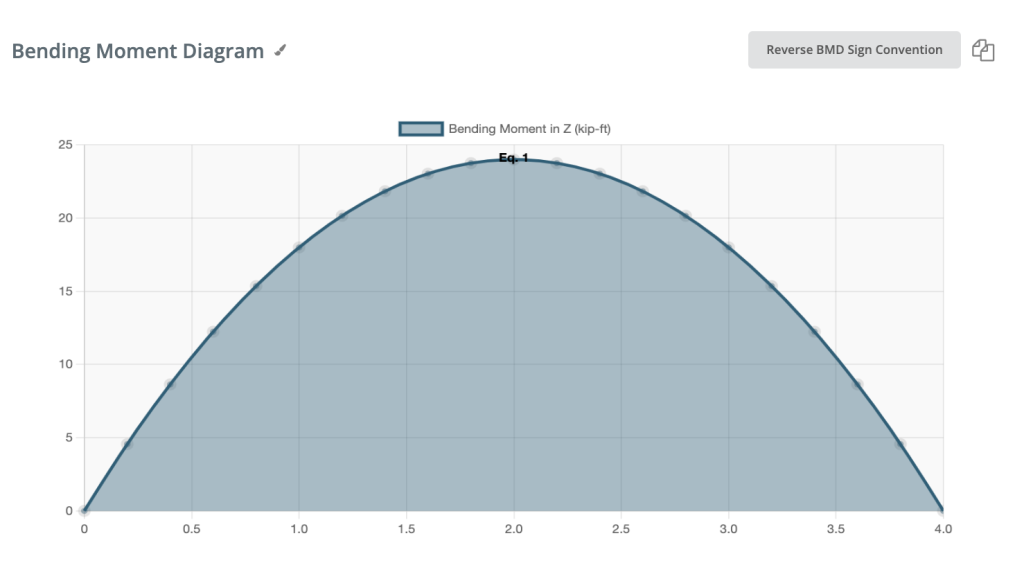
Moment de flexion positif:

Si le moment de flexion est positif, la fibre supérieure de la poutre est comprimée.

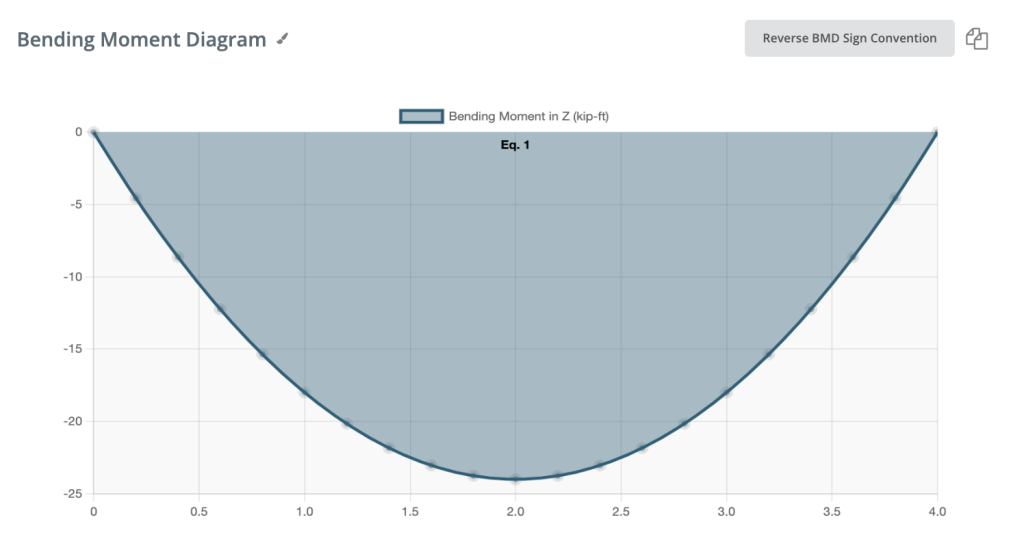
Moment de flexion négatif:

Si le moment fléchissant est négatif, la fibre inférieure de la poutre est comprimée.

Cela a été un guide pour calculer les diagrammes de moments de flexion, si vous voulez en savoir plus sur ce sujet, visitez notre Tutoriels Beam de SkiCiv. Ici vous pouvez trouver de nombreux autres tutoriels utiles tels que formule de contrainte de flexion ou déterminer les réactions aux appuis.

BONUS: Trouver le moment de flexion avec SkyCiv Beam

À l'aide de notre version premium de SkyCiv Beam la calculatrice vous montrera les calculs manuels complets et les étapes prises pour calculer manuellement vos diagrammes de moment de flexion. Modélisez simplement votre poutre à l'aide de la calculatrice, et appuyez sur "Solve". Il vous montrera les calculs étape par étape de la façon à pourvoir dessiner un diagramme de moment de flexion vous même (y compris le positionnement des coupes).