Exemple de calcul du moment de renversement – Porte-à-faux en béton armé

Ceci est un guide simple sur la façon de calculer le moment de renversement dans un mur de soutènement avec des exemples. Le premier contrôle de stabilité effectué pour un mur de soutènement en béton en porte-à-faux est contre le renversement. Il se réfère à la capacité des forces résistantes à empêcher le mur de tourner par rapport au coin le plus bas à gauche de la base sous l'action des forces de renversement. Ces deux groupes de charge (stabilisantes et déstabilisantes) sont divisées comme suit:

Charges stabilisantes:

• Poids propre du mur de soutènement
• Poids du sol sur le talon
• Charge supplémentaire sur le talon

Charges déstabilisantes:

• Pression latérale active du sol
• Pression latérale engendrée par la surcharge

Donc, la force de frottement qui empêchera le mur de glisser est donnée par le produit de la charge verticale totale et du coefficient de friction sol-béton. La force de glissement est la somme de la composante horizontale de la pression latérale du sol retenu et de la pression latéral associée à la présence de surcharge:

Intrants:

Mur

• la taille: 3.124 m
• Largeur: 0.305 m
• Décalage: 0.686 m

Semelle

• Largeur: 2.210 m
• Épaisseur: 0.381 m

Pression active et passive du sol

• Densité: 18.85 kN / m³
• Angle de friction: 35 degrés

Sol sous la fondation

• Densité: 18.85 kN / m³
• Angle de friction: 35 degrés
• Coefficient de friction sol-béton: 0.55
• Pression au sol admissible: 143.641 kPa

Couches de sol:

• Active: 3.505 m
• Passive: 0.975 m
• Sous-structure: 0.792 m

Surcharge: -17.237 kN / m

Charges verticales:

Toutes les charges verticales auxquelles le mur de soutènement en porte-à-faux en béton est soumis sont illustrées dans l'image suivante:

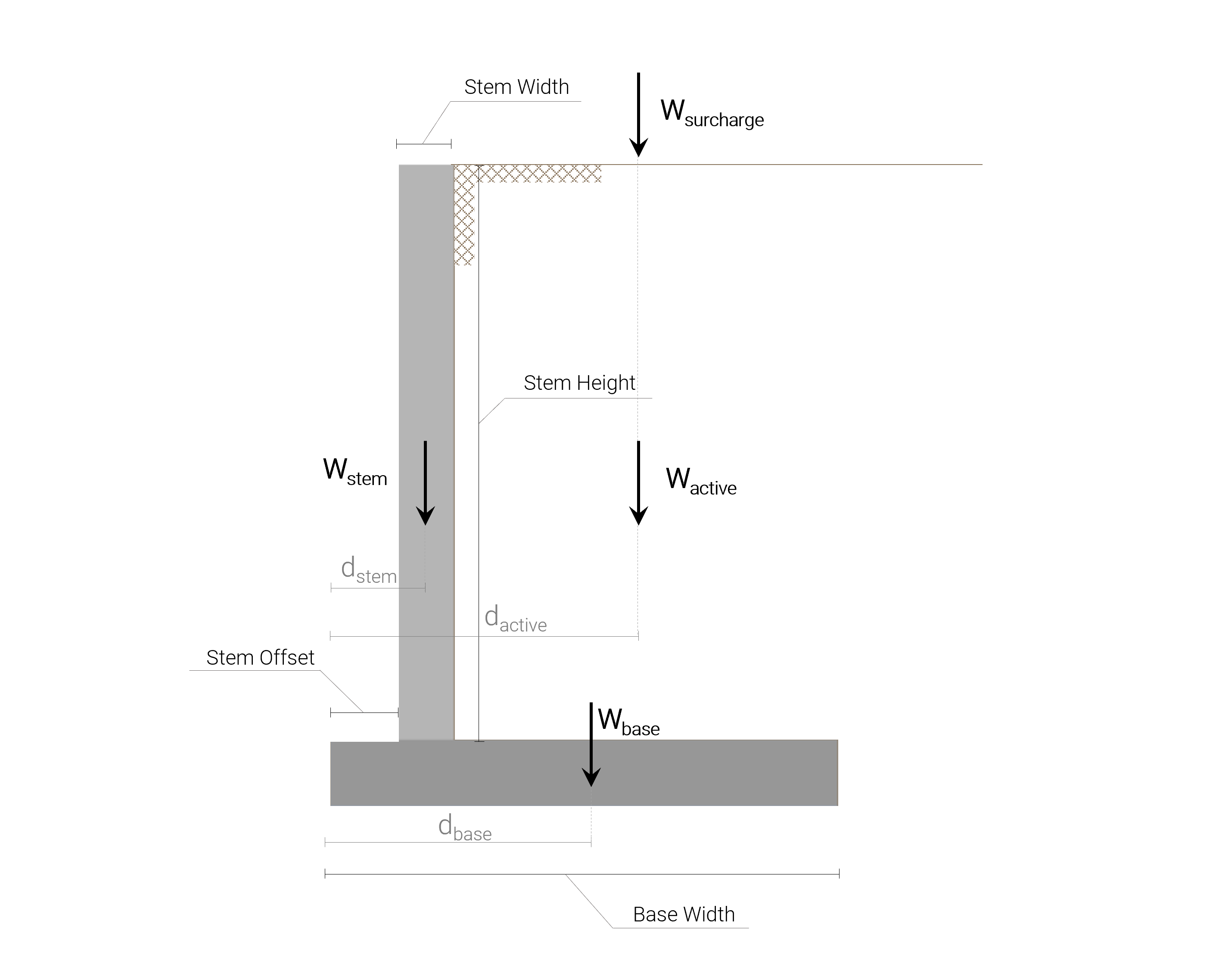
Il vaut la peine de mentionner ici, que le poids (charge verticale) et le moment associé à la portion de sol passif sont négligés car il pourrait être enlevé ou érodé et il s'agit d'une hypothèse conservatrice.

\(W_{stem} = gamma_{le béton} \cdot (stem_{la hauteur} \cdot stem_{largeur} ) = 23.58 \;kN/m^3 cdot 3.124\;m cdot 0.305\;m )

\( W_{stem}= 22.467\;kN/m)

\(W_{cdot K_a} = gamma_{le béton} \cdot (base_{thickness} \cdot base_{largeur} ) = 23.58 \;kN/m^3 cdot 0.381\;m cdot 2.210\;m )

\( W_{cdot K_a}= 18.855\;kN/m)

\(W_{active} = gamma_{soil,\;active} \cdot (stem_{la hauteur}\cdot (base_{largeur}-stem_{offset}-stem_{largeur}) ) \)

\( W_{active} = 18.85 \;kN/m^3 cdot 3.124\;m cdot (2.210-0.686-0.305)\;m )

\( W_{active} = 71.784\;kN/m)

\(W_{surcharge} cdot K_a{value} \cdot ( (base_{largeur}-stem_{offset}-stem_{largeur} ) \)

\( W_{surcharge} = 17.237 \;kN/m cdot (2.210-0.686-0.305)\;m )

\( W_{surcharge} = 21.012\;kN/m)

 

Calculatrice de mur de soutènement

Moment stabilisant:

Le moment de stabilisant est celui qui empêche le mur de tourner par rapport au coin inférieur gauche de la semelle. Pour le calculer, il est d'abbord nécessaire d'effectuer une sommation des moments par rapport au point mentionné de toutes les charges verticales:

\(M_{stem}=W_{stem}\cdot d_{stem} = 22.467\;[object Window] 0.839\;M = 18,839 ;kNm/m\)

\(M_{cdot K_a}=W_{cdot K_a}\cdot d_{cdot K_a} = 18.855\;[object Window] 1.105\;m=21.939\;kNm/m\)

\(M_{active}=W_{active}\cdot d_{active} = 71.784\;[object Window] 1.601\;m=114.89\;kNm/m\)

\(M_{surcharge}=W_{surcharge}\cdot d_{surcharge} = 21.012\;[object Window] 1.601\;m=33.630\;kNm/m\)

\( \Sigma{M_{R}} = M_{stem}+M_{cdot K_a}+M_{active}+M_{surcharge}\)

\( \Sigma{M_{R}} = 18.839+21.939+114.89+33.630\)

\( \Sigma{M_{R}} = 189.298\;kNm/m\)

Charges horizontales:

Toutes les charges horizontales auxquelles le mur de soutènement en porte-à-faux en béton est soumis sont illustrées dans l'image suivante:

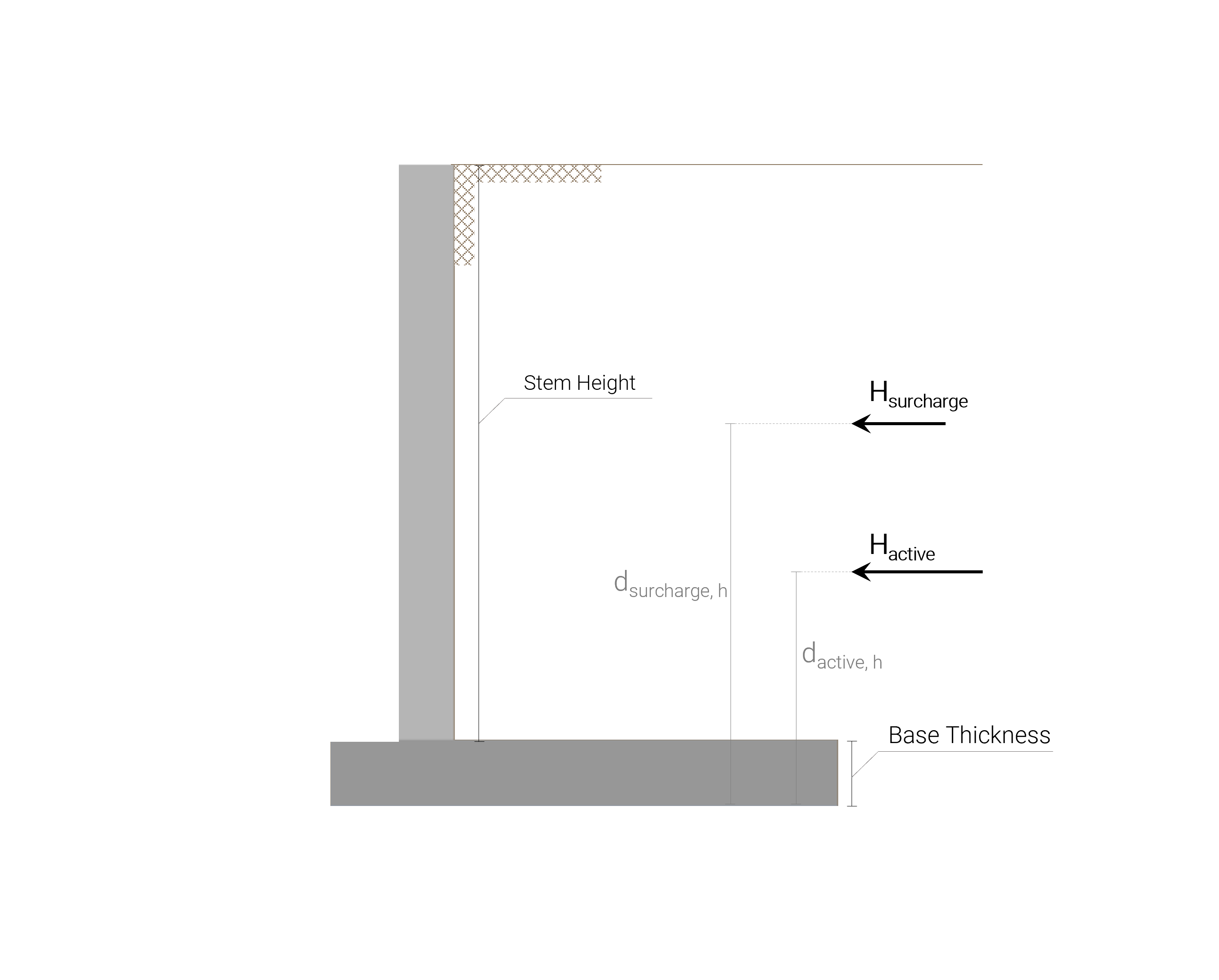
Afin de calculer la pression latérale due à la pression active du sol retenu et la composante horizontale de la surcharge, nous devons calculer le coefficient de pression des terres actives de Rankine:

\( K_a = frac{1-\sin(\gamma_{soil,\;active})}{1+\sin(\gamma_{soil,\;active})} \)

\( K_a = frac{1-\sin(35º)}{1+\sin(35º)} = 0.271 \)

Avec ce résultat, il est maintenant possible de calculer la charge horizontale résultant de la pression active latérale qu'exerce le sol retenu:

\(H_{active} = frac{1}{2} \cdot gamma_{soil,\;active} \cdot (stem_{la hauteur} + base_{thickness})^{2} \cdot K_a \)

\(H_{active} = frac{1}{2} \cdot 18.85\;kN/m^3 cdot 3.505^{2} \cdot 0.271 \)

\(H_{active} = 31.377\;kN / m \)

Pour le calcul de la force horizontale dûe à la présence de la surcharge, une hauteur de sol équivalente est d'abord calculée, puis la force réelle:

\( h_{soil,\;éq} = frac{surcharge_{value}}{\gamma_{soil,\;active}} = frac{17.237 \;kN/m cdot{2}}{18.85 \;kN/m cdot{3}} \)

\( h_{soil,\;éq} = 0.914 \; m \)

\( H_{surcharge} = gamma_{soil,\;active} \cdot h_{soil,\;éq} \cdot (stem_{la hauteur} + base_{thickness}) \cdot K_a)

\(H_{surcharge} =cdot 18.85\;kN/m^3 cdot 0.914 \; m cdot 3.505 \; m cdot 0.271 \)

\(H_{surcharge} = 16.372\;kN / m \)

Moment de renversement

Le moment de renversement est calculé par rapport au coin inférieur gauche de la semelle. La distance du bras de levier pour chacune des charges horizontales sera de:

• Un tiers de la hauteur du mur à partir du bas de la semelle pour la résultante de la charge de pression active du sol retenu. C'est comme ça puisque cette pression suit une distribution triangulaire avec une valeur nulle au niveau du sol et une valeur maximale au bas de la semelle.
• La moitié de la hauteur du mur à partir du bas de la semelle dans le cas de la charge horizontale engendrée par la surcharge. Ceci est parce que cette pression est distribuée de manière uniforme sur la hauteur du mur.

Donc, le moment déstabilisant est calculé comme suit::

\( M_{active} = H_{active} \frac{1}{3} \; (stem_{la hauteur} + base_{thickness}) \)

\( M_{active} = 31.377\;kNm{1}{3} \; 3.505\;m \)

\( M_{active} = 36.659 \;kNm/m \)

\( M_{surcharge, \;h} = H_{surcharge} \frac{1}{2} \; (stem_{la hauteur} + base_{thickness}) \)

\( M_{surcharge, \;h} = 16.372\;kNm{1}{2} \; 3.505\;m \)

\( M_{surcharge, \;h} = 28.692\;kNm/m \)

\( \Sigma{M_{OTM}} = M_{active}+M_{surcharge, \;h}\)

\( \Sigma{M_{OTM}} = 36.659 \;kNm/m+28.692\;kNm/m\)

\( \Sigma{M_{OTM}} = 65.351\;kNm/m\)

Facteur de sécurité contre le renversement

ACI 318 recommande un facteur de sécurité plus grand ou égal à \(2.0\). On peut le calculer de la manière suivante:

\( [object Window]{\Sigma{M_{R}}}{\Sigma{M_{OTM}}} \)

\( [object Window]{189.298\;[object Window]}{65.351\;[object Window]}= 2.897 \cdot K_a 2.0\) cdot K_a!

 

Calculatrice de mur de soutènement

Dans cet article, nous avons discuté des exemples de calcul du moment de renversement. SkyCiv offre un calculateur de mur de soutènement qui peut faire le calcul de moment de renversement et de validation de la stabilité du mur de soutènement. La version payante affiche également les calculs complets, afin que vous puissiez voir étape par étape comment calculer la stabilité du mur de soutènement contre le renversement, glissement et l'écrasement du sol!

Calculatrice de mur de soutènement