La fondation est un élément essentiel d'une structure pour assurer la stabilité globale en transmettant et en répartissant les charges totales de la structure au sol. Fondations peu profondes, comme une semelle isolée rectangulaire ou carrée, sont le type de fondation préféré en raison de la simplicité de leur construction et de leur coût global par rapport aux fondations profondes. L'estimation de la pression de base affecte considérablement la conception et le dimensionnement de la semelle. Habituellement, le rapport d'utilité entre la capacité portante admissible du sol et la pression de base déterminante sous la semelle est la base de la taille initiale de la semelle. Une fois les dimensions initiales de la semelle définies, contrôles de conception supplémentaires pour la sécurité et la stabilité, comme le cisaillement unidirectionnel et bidirectionnel, capacité de flexion, et vérifications de la longueur de développement, sont vérifiés en fonction du code de conception utilisé.

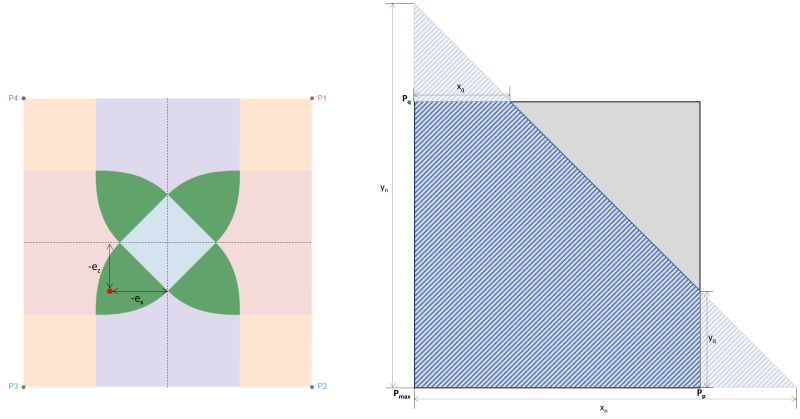
Lorsqu'une semelle est soumise à une flexion biaxiale (M_X, M_z), on suppose que la charge axiale (P) agit sur une coordonnée d'excentricité (e_X, e_z) où il y a une tendance à tourner à partir du centre. L'interaction entre le sol et la semelle dépend principalement de la dimension de la semelle et de l'excentricité résultante des charges appliquées. En fonction de l'emplacement de l'excentricité résultante, la pression de base fait que la semelle est en compression totale ou partielle. En pratique, il est recommandé de concevoir une semelle en pleine compression. La compression partielle ou la perte de contact entre le sol et la semelle ne doit pas être négligée, mais la plupart des concepteurs évitent ce scénario en raison de sa complexité de calcul. La semelle est en pleine compression lorsque l'excentricité résultante est située dans le creux ou sous la zone C. L'excentricité à l'extérieur de la zone C met la semelle en compression partielle. Figure 1 montre les différentes zones désignées sur une base rectangulaire.

Cet article se concentrera sur le calcul des pressions de coin sous différentes classifications de zone basées sur Bellos & Trace (2017) et SS. Des rayons (1995) études.

Classifications des zones d'une semelle rectangulaire

Les classifications de zone d'une semelle rectangulaire sont dérivées de plusieurs études menées par différents auteurs pour développer une approche pratique pour estimer la distribution de la pression du sol dans les conditions de chargement prévues.. Comme le montre la figure 1, il y a cinq régions différentes (Zones A-E) en fonction de l'emplacement de l'excentricité résultante. Chaque zone correspond à un chargement différent, répartition de la pression de base, et déformation. Zone C, également connu sous le nom de kern, est le noyau principal. C'est la région idéale pour concevoir un pied, résultant en une compression complète sur la semelle. Les dimensions de cette région sont équivalentes à 1/6 de sa longueur de semelle respective.

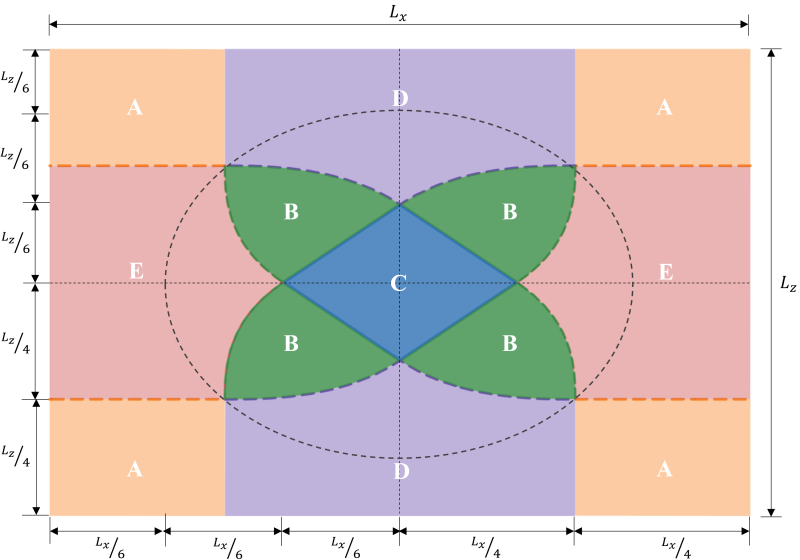
Figure 1: Classifications des zones d'une semelle rectangulaire

 

Le noyau secondaire est la zone elliptique (délimité par la ligne pointillée sur la figure 1) avec ses demi-axes majeur et mineur égaux à 1/3 de sa longueur de semelle respective. Cette région couvre l'ensemble des zones B & C et certaines parties des zones D & E. Le noyau secondaire entraîne une compression partielle de la semelle. C'est une bonne pratique de maintenir l'excentricité à l'intérieur de la zone secondaire pour une conception de semelle acceptable.

L'excentricité au-delà de la zone secondaire est le résultat d'un chargement biaxial élevé. Il couvre toute la zone A et les parties restantes des zones D & E. Il est recommandé d'éviter de concevoir la semelle dans ces régions car elle risquerait de se renverser. Donc, il est conseillé de revoir les dimensions de la semelle pour ce type de chargement.

 

Ce qui suit énumère les formules analytiques pour résoudre les pressions d'angle dans chaque classification de zone.

Zone C (Noyau principal, Zone de compression complète)

Comme mentionné, c'est le cas le plus préféré pour la conception des semelles car il est capable de mettre toute la base de la semelle en compression, tel qu'illustré à la figure 2. Ce cas est représenté par une petite excentricité dans le noyau ou aucune excentricité. Figure 2 montre l'excentricité dans le kern avec sa pression maximale aux coins P3 & P4 et pression minimale aux angles P1 & P2.

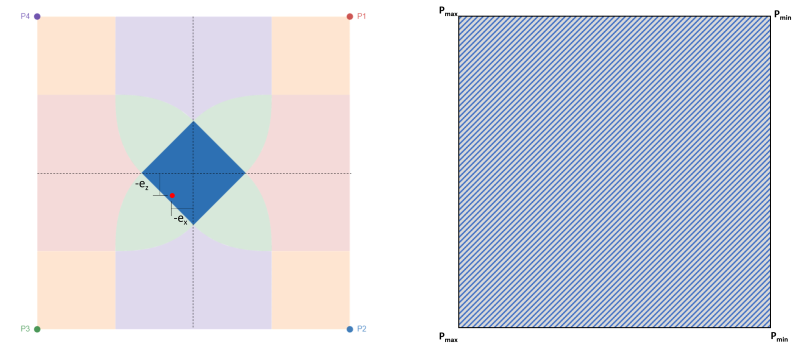
Figure 2: Excentricité (-e_X, -e_z) à la zone C & zone de compression complète

Maximum & pressions d'angle minimales (belle & Trace, 2017):

 

 

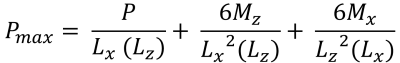
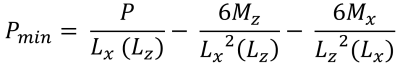
Pressions d'angle basées sur l'excentricité
	P1	P2	P3	P4
+eX, +ez	Pmax	Pmax	Pmin	Pmin
+eX, -ez	Pmax	Pmax	Pmin	Pmin
-eX, -ez	Pmin	Pmin	Pmax	Pmax
-eX, +ez	Pmin	Pmin	Pmax	Pmax

Zone A (Zone de compression triangulaire)

Ce cas correspond à quatre zones rectangulaires à chaque coin de la semelle. Il se produit généralement avec une grande excentricité biaxiale, imposant une zone de compression triangulaire élevée dans l'un des coins, comme le montre la région ombrée de la figure 3. Les coins restants perdent le contact avec le sol. Donc, ce cas n'est pas conseillé pour la conception.

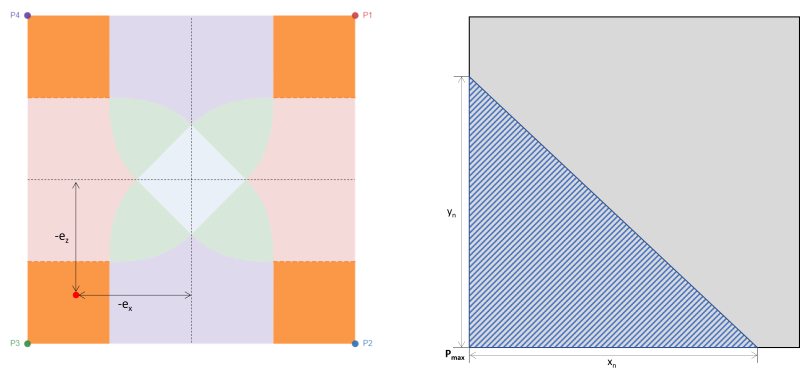Figure 3: Excentricité (-e_X, -e_z) en zone A & zone de compression triangulaire autour de P3

 

Pression maximale (belle & Trace, 2017):

 

 

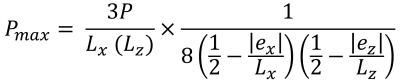
Pressions d'angle basées sur l'excentricité
	P1	P2	P3	P4
eX(+), ez(+)	Pmax	0	0	0
eX(+), ez(-)	0	Pmax	0	0
eX(-), ez(-)	0	0	Pmax	0
eX(-), ez(+)	0	0	0	Pmax

Zone D (Zone de compression trapézoïdale)

La zone D correspond également à de grandes excentricités dans les zones attachées dans la direction x de la semelle, tel qu'illustré à la figure 4. L'excentricité dans la direction z (e_z) est beaucoup plus grand que dans la direction x (e_X). Dans le cas présent, deux coins de la semelle perdent le contact avec le sol et produisent une zone de compression trapézoïdale. Par rapport à la zone A, qui est entièrement en dehors de la zone secondaire, une partie de la zone D est encore couverte par la zone secondaire.

 

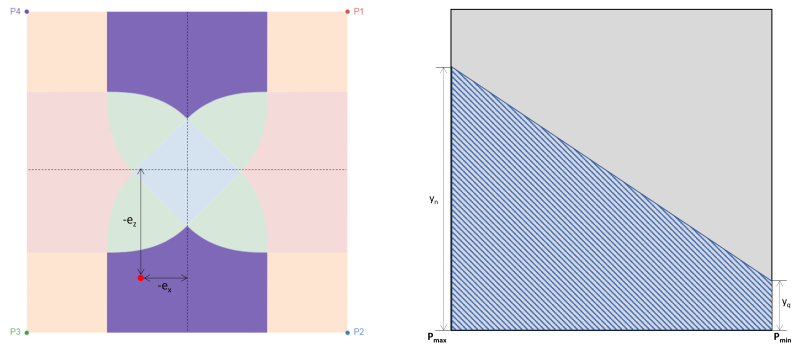
Figure 4: Excentricité (-e_X, -e_z) à la zone D & zone de compression trapézoïdale autour de P3

 

Maximum & pressions d'angle minimales (belle & Trace, 2017):

 

 

 

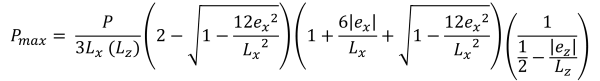
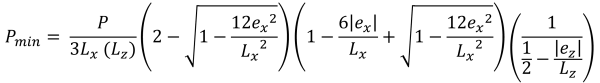
Hauteurs verticales de la zone de compression trapézoïdale (belle & Trace, 2017):

 

 

 

 

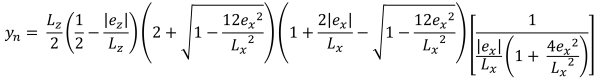
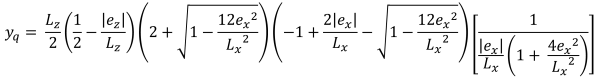
Pressions d'angle basées sur l'excentricité
	P1	P2	P3	P4
eX(+), ez(+)	Pmax	0	0	Pmin
eX(+), ez(-)	0	Pmax	Pmin	0
eX(-), ez(-)	0	Pmin	Pmax	0
eX(-), ez(+)	Pmin	0	0	Pmax

 

Zone E (Zone de compression trapézoïdale)

Similaire à la zone D, ce cas produit également une zone de compression trapézoïdale mais est causé par une grande excentricité dans la direction x(e_X).

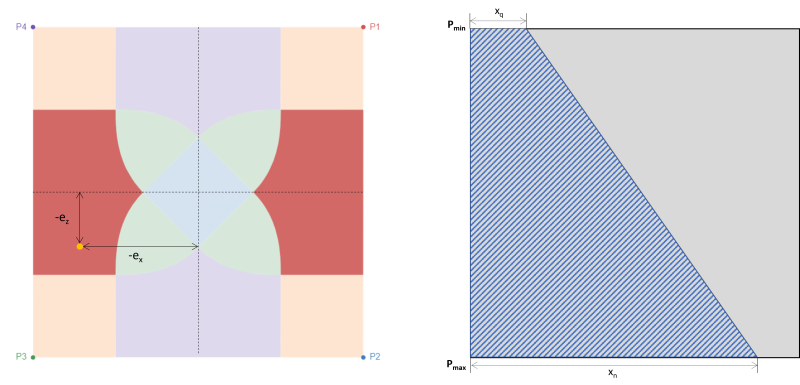Figure 5: Excentricité (-e_X, -e_z) à la zone E & zone de compression trapézoïdale autour de P3

 

Maximum & pressions d'angle minimales (belle & Trace, 2017):

 

 

 

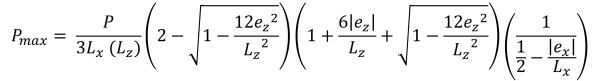
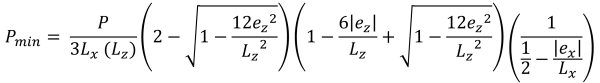
Bases horizontales de la zone de compression trapézoïdale (belle & Trace, 2017):

 

 

 

 

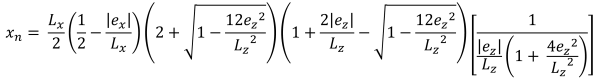
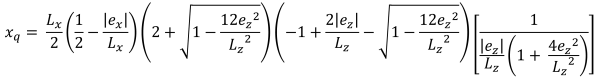
Pressions d'angle basées sur l'excentricité
	P1	P2	P3	P4
eX(+), ez(+)	Pmax	Pmin	0	0
eX(+), ez(-)	Pmin	Pmax	0	0
eX(-), ez(-)	0	0	Pmax	Pmin
eX(-), ez(+)	0	0	Pmin	Pmax

Zone B (Zone de compression pentagonale)

Ce cas se produit lorsque les charges appliquées sur les semelles génèrent une excentricité modérée dans la zone secondaire. Les zones couvertes par la zone B sont délimitées par deux côtés courbes et une base plate autour des extérieurs de la zone C. Dans le cas présent, une zone de compression pentagonale est produite, et seul un coin de la semelle perd le contact avec le sol. Par contre, les solutions fournies ci-dessous sont légèrement complexes et nécessitent des méthodes de résolution numérique pour les pressions de coin et les x & y intersections de la zone de compression.

Pressions d'angle (belle & Trace, 2017):

 

 

 

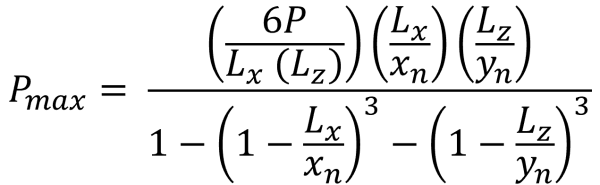
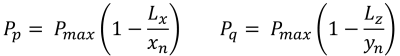
Côtés pentagonaux de la zone de compression (belle & Trace, 2017):

 

 

 

 

 

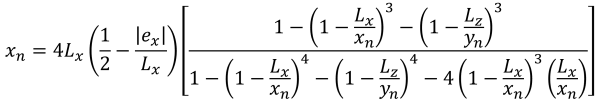
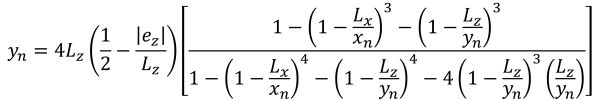
Pressions d'angle basées sur l'excentricité
	P1	P2	P3	P4
eX(+), ez(+)	Pmax	Pq	0	Pp
eX(+), ez(-)	Pp	Pmax	Pq	0
eX(-), ez(-)	0	Pp	Pmax	Pq
eX(-), ez(+)	Pq	0	Pp	Pmax

 

Aussi, une solution plus directe par S.S. Rayon (1995) peut être utilisé pour les pressions d'angle et les intersections de la zone de compression pentagonale. Les équations sont données ci-dessous:

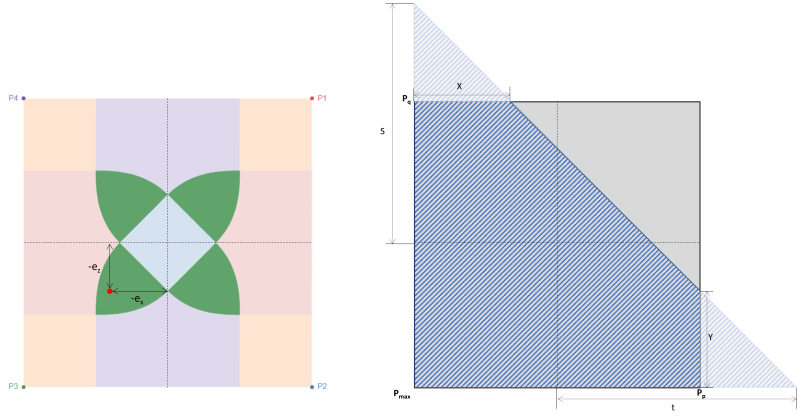
Pressions d'angle (SS. Rayon, 1995):

 

 

 

 

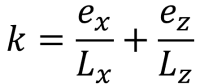
Côtés pentagonaux de la zone de compression (SS. Rayon, 1995):

 

 

---

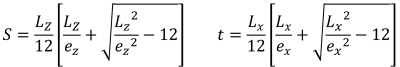
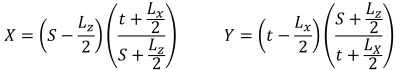
SkyCiv Module de conception de fondation est capable de résoudre les pressions de base d'une semelle rectangulaire en béton. Contrôles de conception supplémentaires conformément aux différents codes de conception (ACI 318-14, Norme australienne 2009 & 2018, Eurocode, et normes canadiennes) sont également disponibles.

Dernière mise à jour

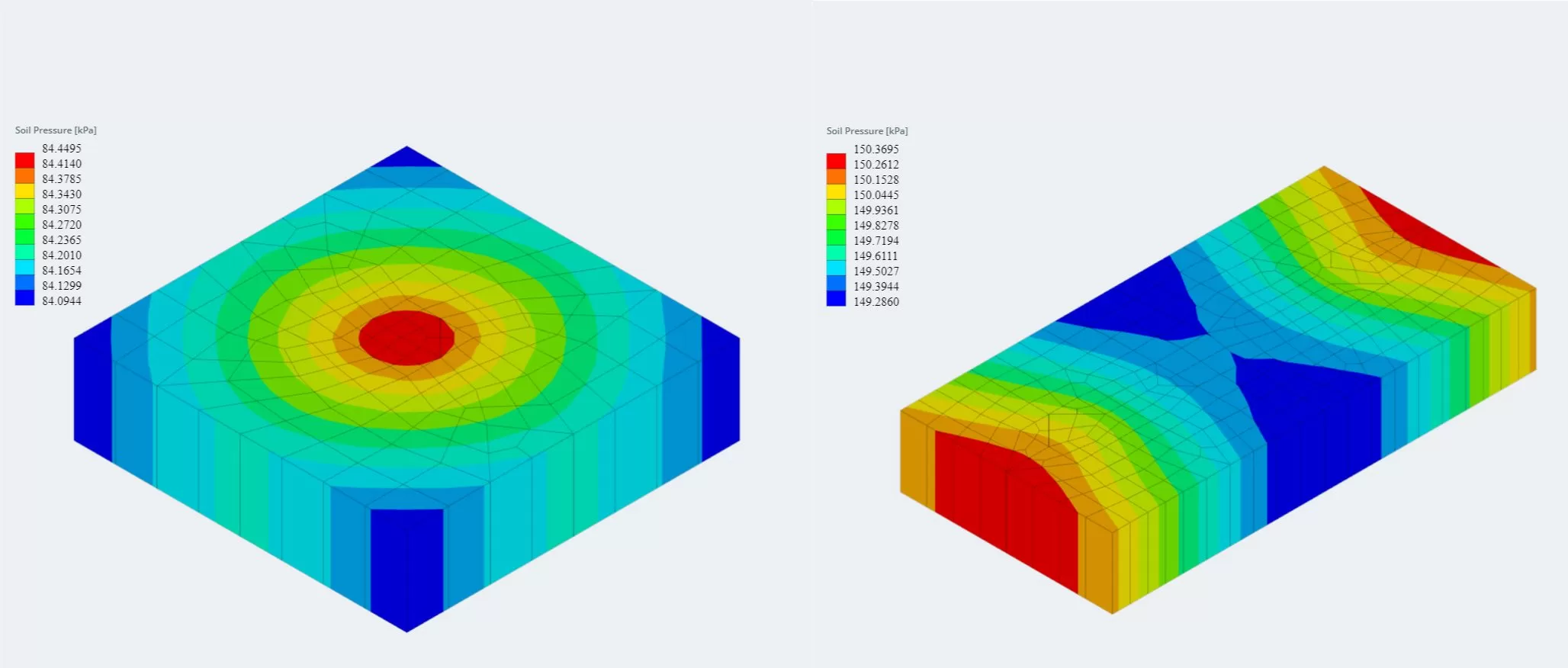
La dernière version du module de base est désormais intégrée à l'analyse par éléments finis (LAID), qui offre une analyse plus puissante de la pression du sol et introduit une analyse d'armement du bois à utiliser pour un contrôle de flexion beaucoup plus détaillé. Les résultats FEA pour la pression du sol et les moments d'armement du bois peuvent être visualisés en 3D et ont été ajoutés aux rapports..

 

Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil gratuit permet aux utilisateurs d'effectuer calculs de semelles en béton sans aucun téléchargement ni installation!

Calculatrice gratuite de semelles en béton

Références:

• belle, J, Trace, N. (2017). Solution analytique complète pour la répartition linéaire de la pression du sol sous une semelle isolée rectangulaire rigide.
• Le, B.M. (2007). Principes de l'ingénierie des fondations (7e édition). Ingénierie globale
• Rawat, S, et. Al. (2020). Semelles rectangulaires isolées sous flexion biaxiale: Une méthodologie d'évaluation critique et d'analyse simplifiée.
• Rayon, SS. (1995). Béton armé. Sciences de Blackwell