Calculateur Gratuit de Centroïde et de Moment d'Inertie
Calculer le Moment d'Inertie, le Centroïde, et le Module Élastique pour diverses sections
Le Guide complet du Calculateur de Moment d'Inertie
Le calculateur de Centroïde et de Moment d'Inertie de Skyciv vous permet de déterminer le moment d'inertie, le centroïde, et d'autres propriétés géométriques pour une variété de sections, y compris les rectangles, les cercles, sections creuses, les triangles, les poutres en I, les poutres en T, les cornières et les profilés en C. Nous avons également quelques articles ci-dessous décrivant la méthode de calculer le moment d'inertie, ainsi que des informations supplémentaires sur le calcul du centroïde et du module élastique.
Vous pouvez utiliser le calculateur sur trois sections avant de devoir vous inscrire pour un compte gratuit - ce qui vous donnera aussi accès à plusieurs autres logiciels d'analyse.. Avec le compte payant, vous avez de plus accès à la démarche complète. Vous pouvez ainsi analyser la façon dont le calculateur arrive à ses résultats.. Consulter la section sous la calculatrice pour plus d'informations à ce sujet, ainsi que des liens vers d'autres outils et fonctionnalités offerts par SkyCiv.
Comment utiliser le calculateur de moment d'inertie SkyCiv
Visionnez la vidéo ci-dessous pour débuter immédiatement avec notre calculateur de Moment d'Inertie..
Choisissez simplement la section que vous souhaitez évaluer dans le menu déroulant, entrez les dimensions de votre section choisie et appuyez sur Calculer.
Cette calculatrice polyvalente gratuite fait partie intégrante de notre suite complète de logiciels d'analyse structurelle. Elle vous permet, entre-autre, de:
- Calculer le moment d'inertie (I) de la section d'une poutre (Moment quadratique)
- Calculer le centroïde (C) dans les axes X et Y d'une section de poutre
- Calculer le premier moment d'aire (Moment Statique) (Q) de la section d'une poutre
- Un calculateur de module d'élasticité pour calculer le module d'élasticité (Z) de la section d'une poutre
- Calculer la constante de torsion (J) de la section d'une poutre
Définitions communes des propriétés de section
Le calculateur de moment d'inertie calcule avec précision certaines propriétés géométriques importantes utilisées pour l'ingénierie des structures. Voici une liste des symboles et définitions utilisées pour le calcul des propriétés d'une section:
- Aire de la section (A) – La surface de la section est un calcul assez simple, toutefois très utile dans les calculs de contraintes axiales (plus l'aire est élevée, plus la résistance axiale est élevée)
- Moment d'inertie (Iz, Iy) - également connu sous le nom de deuxième moment de l'aire, est une propriété utilisée pour déterminer la résistance d'un élément et sa résistance à la déflexion. Plus ce nombre est élevé, plus la section est raide. Il est calculé autour de deux axes:
- Axe des X (Iz) - Ceci concerne l'axe Z et est généralement considéré comme l'axe principal car il s'agit généralement de la direction la plus forte de l'élément
- Axe des Y (Iy) – L'axe Y et est considéré comme l'axe secondaire ou l'axe faible. Les sections ne sont généralement moins résistances autour de cet axe
- Notons également que si une section a les mêmes dimensions selon les deux axes (carrée, circulaire, etc.) ces valeurs seront les mêmes selon les deux axes. Se référer au moment d'inertie d'un cercle pour plus d'information.
- le Centroïde (Cz, Cy) – c'est le centre de gravité de la section et a généralement une composante Z et Y. Pour les formes symétriques, il correspond au centre géométrique. Pour les formes non symétriques (comme la cornière, le profilé en C) ceux-ci sont à des endroits différents. Pour apprendre à calculer le centre de gravité d'une section de poutre, voir ci-dessus.. La calculatrice ci-dessus permet également de calculer les centroïdes X et Y de tout type de forme..
- Moment Statique (Qz, Qy) - Aussi connu sous le nom de premier moment de la zone, ceci mesure la distribution de l'aire d'une section de poutre par rapport à un axe.. Comme le moment d'inertie, ceux-ci sont à la fois dans les directions Z et Y. Ceux-ci sont généralement utilisés dans les calculs de contrainte de cisaillement, donc plus cette valeur est élevée, plus la section est résistante au cisaillement. Le calculateur fournira cette valeur, mais cliquez ici pour en savoir plus sur le calcul du premier moment d'aire.
- Module élastique (Sz, Sy en Amérique. Zz, Zy en Grande-Bretagne ou en Australie) – Également connu sous le nom de module de section statique, ils sont utilisés dans les calculs de contrainte de flexion. Ils sont généralement calculés pour les fibres supérieures et inférieures de la section.. Par exemple, Szt est le module élastique autour de l'axe Z calculé par rapport à la fibre supérieure..
- Constante de torsion (J) – également connu sous le nom de moment d'inertie polaire ou J, c'est une valeur qui décrit la résistance d'un matériau à la torsion ou à la déformation par torsion.
- Le module plastique (S) – une mesure de la capacité d'une forme de section transversale à résister à la flexion plastique, utilisé pour estimer la contrainte d'un matériau lorsqu'il commence à céder (atteindre sa limite plastique) sous une charge spécifique et est généralement utilisé pour la conception et l'analyse des poutres sous charge.
Autres paramètres - Ces résultats plus avancés sont calculés par le générateur de section SkyCiv:
- Moment quadratique polaire (par rapport aux axes Z et Y): Une mesure de la résistance d'une forme à la rotation autour d'un axe spécifique, égal au produit croisé de la distance entre l'axe et tout point de la forme et la composante correspondante du moment d'inertie du point.
- Module de section en plastique (par rapport aux axes Z et Y): Une mesure de la capacité d'une forme de section transversale à résister à la flexion plastique, utilisé pour estimer la contrainte d'un matériau lorsqu'il commence à céder (atteindre sa limite plastique) sous une charge spécifique.
- Axe neutre en plastique (par rapport aux axes Z et Y): Un axe dans une forme de section transversale par lequel toutes les forces agissant sur la forme doivent passer afin d'entraîner une déformation plastique.
- Aire de cisaillement (par rapport aux axes Z et Y): L'aire de la section efficace pour résister aux forces de cisaillement.
- Distance du centre de cisaillement au centre de gravité (dans les deux axes Z et Y): Le calculateur de centre de gravité SkyCiv permet de calculer la distance entre le centre de cisaillement et le centre de gravité d'une section.
- Constante de torsion (Utilisation de l'analyse par éléments finis): Une valeur qui décrit la résistance d'un matériau à la torsion ou à la déformation par torsion, calculé à l'aide de l'analyse par éléments finis.
- Rayon de torsion: La distance à partir d'un axe à laquelle l'aire d'une section doit être concentrée pour aboutir à la même constante de torsion que celle de la forme réelle.
- Constante de gauchissement: Une valeur qui décrit la résistance d'un matériau au gauchissement ou à la déformation par distorsion.
- Constante de monosymétrie (par rapport aux axes Z et Y): Une mesure de la symétrie d'une forme de section transversale autour d'un axe spécifique, avec une valeur de zéro indiquant une symétrie parfaite.
- Rayon de giration (par rapport aux axes Z et Y): La distance à partir d'un axe à laquelle l'aire de la forme de section transversale doit être concentrée pour donner le même moment d'inertie que la forme réelle.
- Angle de rotation des axes principaux: L'angle entre l'axe neutre et l'axe principal d'une section.
À propos du moment d'inertie, des centres de gravité et autres propriétés de section
Nous avons également compilé plus d'informations pour calculer le moment d'inertie des sections. Ce guide complet devrait aider à fournir une base de connaissances complète pour tout ce qui concerne le moment d'inertie, centroïdes, le module élastique et les autres propriétés de section géométriques. Dans les sections ci-dessous, nous expliquons ce qu'est le moment d'inertie, comment calculer le centroïde, le moment d'inertie ainsi que d'autres équations à l'aide de la calulatrice de moment d'inertie SkyCiv..
Qu'est-ce que le moment d'inertie?
Le moment d'inertie (plus spécifiquement connu sous le nom de moment quadratique, ou le deuxième moment de l'aire) est une propriété géométrique importante utilisée en ingénierie des structures. Il est directement lié à la résistance en flexion de votre section.
En général, plus le moment d'inertie est élevé, plus votre section est raide, et par conséquent moins il fléchira sous charge. Le moment d'inertie d'une section rectangulaire, ou de toute autre forme, mesure techniquement la quantité de couple nécessaire pour accélérer la masse autour d'un axe - de là le mot "inertie"..
Comment trouver le moment d'inertie - Rectangulaire
Pour calculer le moment d'inertie d'une section rectangulaire, nous pouvons utiliser la formule simplifiée:
I = (b * h ^ 3) / 12
I est le moment d'inertie du rectangle
b est la largeur du rectangle
h est la hauteur du rectangle
Il est important de noter que les unités de mesure pour b et h doivent être consistantes. (i.e., pouces, millimètres, etc.). L'unité de mesure du résultat final dépend également de l'unité de mesure des paramètres d'entrée, . Par exemple, si l'unité d'entrée est en mètre, l'unité de mesure du résultat serait m ^ 4.
Exemple de calcul du moment d'inertie
Disons que nous avons un rectangle avec les dimensions suivantes:
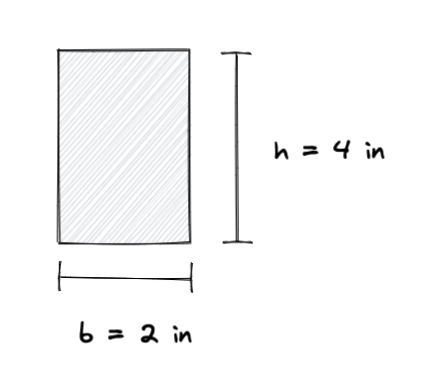
Utilisant la formule du moment d'inertie, on peut calculer le moment d'inertie du rectangle comme suit:
I = (b * h ^ 3) / 12
I = (2 * 4^ 3) / 12
I = (2 * 64) / 12
= 10.67 in ^ 4
Donc le moment d'inertie du rectangle est de 10.67 pouce ^ 4. Ce moment d'inertie est autour de l'axe qui passe par le centroïde, rappelez-vous que si vous avez besoin de trouver le moment d'inertie autour d'un axe différent, vous devrez utiliser une formule différente ou effectuer une transformation. Vous pouvez également vérifier que l'unité de mesure du résultat est toujours les unités d'entrée à la puissance 4., Dans ce cas, toutes les unités d'entrée sont en pouces, donc le résultat est en pouces ^ 4.
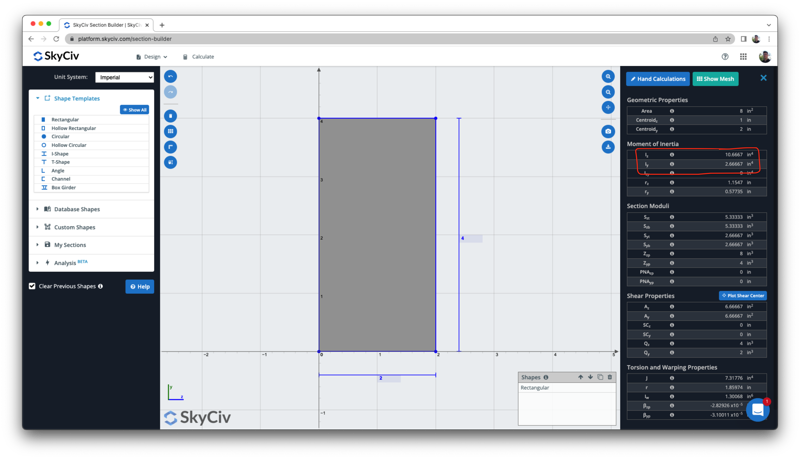
Nous pouvons vérifier ce résultat avec le calculateur de moment d'inertie gratuit ci-dessous, qui donne le même résultat de 10.6667 in ^ 4:
Comment trouver le moment d'inertie - Je rayonne
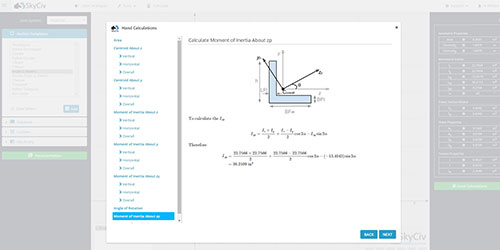
Examinons maintenant un cas plus complexe où la section est une poutre en I, avec différentes dimensions d'ailes. Le concept est le même, cependant l'approche dans ce cas est différente. En bref, nous devons considérer la section en I comme une combinaison de différents rectangles et additionner les différentes parties pour obtenir le moment d'inertie complète.. En bref, nous devons suivre trois étapes:
- Calculer l'axe neutre pour toute la section
- Calculer le moment d'inertie de chaque pièce
- Calculer le moment d'inertie global à l'aide du théorème des axes parallèles - qui est essentiellement la somme des moments d'inertie individuels
Considérons donc la section suivante:
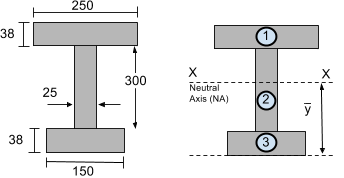
L'axe neutre (A.N.) est situé au centre de gravité. Il s'agit essentiellement d'une moyenne pondérée du produit de l'aire et de la distance de la base pour chaque segment. Nous avons simplement besoin d'utiliser l'équation du centre de gravité pour calculer le centre de gravité à orientation verticale (Y) d'une section avec plusieurs segments.

Nous prendrons la ligne de référence du bas de la section de poutre. Trouvons maintenant Ai et yi pour chaque segment de la section de poutre en I illustrée ci-dessus afin que le centroïde vertical (axe Y) puisse être trouvé.


Nous avons maintenant le centre de gravité. Poursiuvons avec le moment d'inertie. Pour calculer le moment d'inertie total de la section, nous devons utiliser le "Théorème des axes parallèles" tel que défini ci-dessous:

Étant donné que nous avons divisé notre section en trois parties rectangulaires, il faut calculer le moment d'inertie de chacune de ces sections. Nous pouvons maintenant utiliser la formule simplifiée du moment d'inertie rectangulaire:
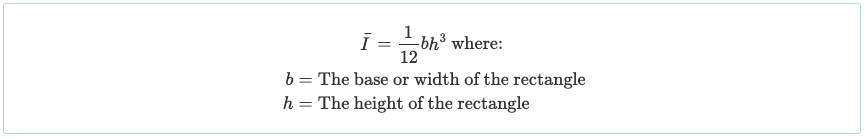
Nous avons maintenant toutes les informations nécessaires pour utiliser le "Théorème des axes parallèles" et trouver le moment d'inertie total de la section de notre poutre en I. Dans notre exemple de moment d'inertie est calculé comme suit:

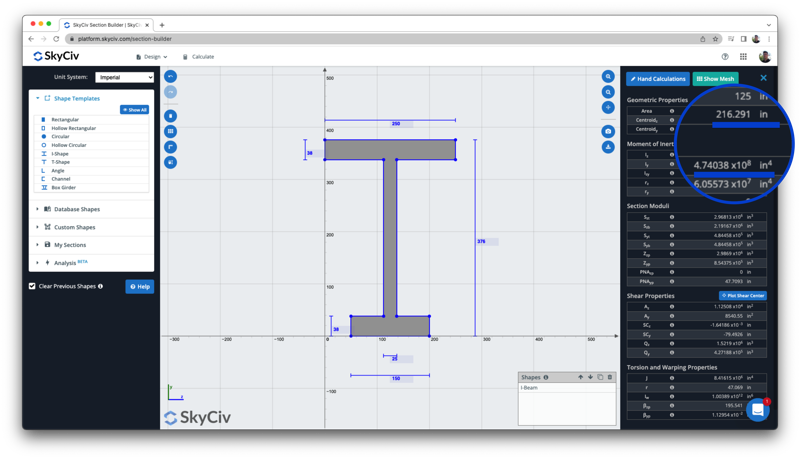
Encore une fois, nous pouvons comparer ce résultat avec celui du calculateur de moment d'inertie gratuit pour comparer les résultats du centroïde et du moment d'inertie, où le centre de gravité (216.29 in) et le moment d'inertie (4.74 x 10 ^ 8 po ^ 4) sont identiques:
Pour plus d'informations, visitez notre tutoriel sur Calcul du moment d'inertie d'une section de poutre.
Équations de moment d'inertie
Des équations simples peuvent également être utilisées pour calculer le moment d'inertie de formes et de sections courantes. Ce sont des équations de moment d'inertie rapides qui fournissent des valeurs rapides et sont un excellent moyen contrevalider ou de vérifier vos résultats. Portant uniquement sur des formes simples, le diagramme ci-dessous montre certaines de ces équations:
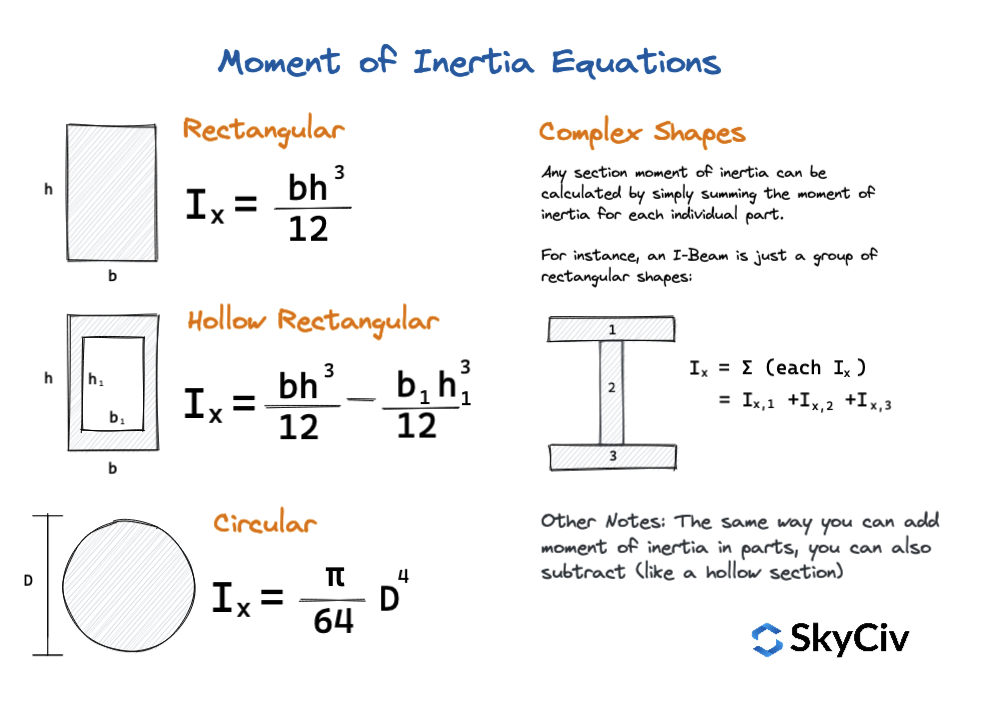
Calculateur de centroïde SkyCiv
Le centroïde, également connu sous le nom de "centre géométrique", est le centre de masse d'un objet de densité uniforme. Un exemple simplifie d'un centroïde, serait l'endroit où vous auriez besoin de placer un crayon pour le garder en équilibre sur votre doigt. Le point où le crayon est parfaitement balancé sur votre doigt est l'emplacement approximatif du centroïde du crayon. La masse et la densité du matériau de part et d'autre de votre doigt doivent être égales pour atteindre cet équilibre, et représente donc le 'centre de masse' du crayon.
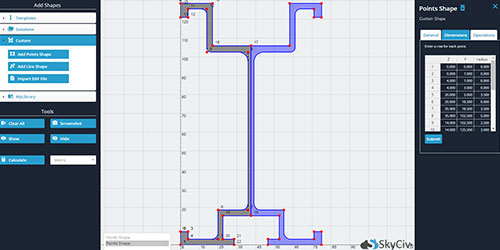
La calculatrice SkyCiv Centroid utilise l'analyse par éléments finis pour fournir des résultats très précis en quelques secondes, quelle que soit la complexité de la forme. Dans la version premium, les utilisateurs peuvent entrer les coordonnées des points qui définissent une forme quelconque et la calculatrice vous calculera les coordonnées du centre de gravité. Ceci permet de concevoir des formes personnalisées via l'importation DXF, sections multiples (assemblages) ou autre formes génériques.
En plus de sa rapidité et sa précision, notre calculateur centroïde est également incroyablement facile à utiliser. Avec une interface simple, vous pouvez entrer les dimensions de votre section et recevoir les valeurs de ses propriétés (y compris le centre de gravité de la section) en quelques secondes. Que vous travailliez sur un projet de conception, expérimentiez avec différentes sections ou étudiiez pour un examen, le calculateur SkyCiv Centroid est l'outil parfait pour vous aider à faire le travail.
Calculateur de module de section élastique
Tel que mentionné précédemment, cet outil gratuit vous fournit également une calculatrice de module élastique, cependant, si vous débutez en tant qu'ingénieur, vous ne comprendrez peut-être pas ce qu'est le module élastique. En bref, le module élastique est une propriété de section qui indique la résistance à la flexion et qui correspond au quotien entre le moment d'inertie et la distance entre l'axe neutre et la fibre la plus éloignée. Le module élastique est représenté par l'équation qui suit:
Où,
- S est le module élastique
- I est le moment d'inertie de la section par rapport à l'axe neutre
- y est la distance entre l'axe neutre et la fibre extrême de la section
Il existe deux types de module de section: Élastique et Plastique. En Amérique, S est généralement utilisé pour désigner le module de section élastique, tandis que Z est utilisé pour désigner le module de section plastique.. En Grande-Bretagne et en Australie, ceux-ci sont généralement inversés. Le module de section élastique est généralement désigné par une lettre Z, tandis que le module de section plastique est désigné par une lettre S.
En général, le module de section élastique est utilisé pour la conception de section, car il est applicable jusqu'à la limite d'élasticité pour la plupart des métaux. Les métaux ne sont généralement pas conçus pour aller au-delà de la limite d'élasticité du matériau.
Documents supplémentaires
Veuillez vous référer aux pages de documentation suivantes pour des informations plus détaillées sur les propriétés des sections, comment les calculer pour différentes formes, et comment utiliser notre calculatrice centroïde:
Autres outils gratuits
SkyCiv propose également d'autres outils tels que l'outil de dimensionnement de poutre I et un logiciel de conception structurelle gratuit. Le outil de dessin de section vous montrera également une représentation graphique de votre section de poutre en temps réel. Donc, si vous voulez calculer le moment d'inertie d'une section circulaire, le moment d'inertie d'un rectangle ou de toute autre forme, n'hésitez pas à utiliser les outils ci-dessous ou notre générateur de sections SkyCiv.
SkyCiv propose une large gamme de logiciels de conception et d'analyse structurelle en cloud pour les ingénieurs. En tant qu'entreprise technologique en constante évolution, nous nous engageons à innover et à remettre en question les méthodes de travail existantes pour faire gagner du temps aux ingénieurs dans leurs processus de travail et leurs conceptions.
Besoin de plus de fonctionnalités?
Passer à un compte plan professionnel pour débloquer toutes les fonctionnalités