Présentation pas à pas des calculs pour concevoir une semelle isolée (AS 3600 2018)

La fondation est un système de construction essentiel qui transfère les forces des colonnes et des murs au sol porteur. L'ingénieur peut opter pour un système de fondation peu profonde ou profonde en fonction des caractéristiques du sol et des charges du bâtiment..

Module de conception de la Fondation SkyCiv comprend l'analyse et la conception de semelles isolées conformes aux normes australiennes (AS 3600 2009 & 2018).

 

 

Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil permet aux utilisateurs d'effectuer des calculs de charge sans téléchargement ni installation!

Calculatrice de semelles en béton

Conception d'une semelle isolée

---

Exigences de dimension

Pour déterminer les dimensions d'une semelle isolée, service ou charges non pondérées, comme une action permanente (g), action imposée (Q), action du vent (W_u), action de tremblement de terre (E_u), et S_u sera appliqué à l'aide de combinaisons de charges, tel que défini par AS 3600. La combinaison de charges qui régit sera considérée comme la charge de conception, et est comparée à la pression du sol admissible comme indiqué dans l'équation 1.

\(\texte{q}_{\texte{a}} = frac{\texte{P}_{\texte{n}}}{\texte{A}} \flèche droite \) Équation 1

q_a = pression du sol admissible
P_n = charges de conception du niveau de service
A = surface de fondation

Les dimensions de la semelle peuvent être initialement estimées en résolvant la surface de la fondation (A) en utilisant l'équation 1.

\(\texte{A} = frac{\texte{P}_{\texte{n}}}{\texte{q}_{\texte{a}}} \flèche droite \) Équation 1a

Cisaillement unidirectionnel

Le cisaillement unidirectionnel état limite, aussi connu sous le nom cisaillement en flexion, reconnaît que la semelle peut se rompre sous un cisaillement similaire à celui d'une poutre large le long d'un plan de cisaillement critique situé à une certaine distance “d” de la face de la colonne (Figure 1), basé sur Clause AS3600 8.2.7.1

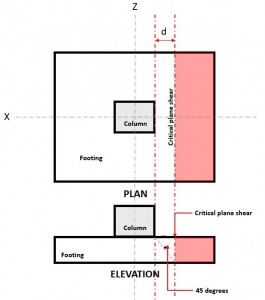
Figure 1. Plan de cisaillement critique du cisaillement unidirectionnel

Le Une manière Tondre Demande ou V_u est calculé en supposant que la semelle est en porte-à-faux par rapport au poteau là où la zone rouge est indiquée sur la figure 1.

Le Une manière Tondre Capacité ou Vu_c est définie comme la résistance ultime au cisaillement et calculée à l'aide de l'équation 2 par AS3600-09 Cl 8.2.7.1.

\( \phi texte{V}_{uc} = phi beta_{1} \fois beta_{2} \fois beta_{3} \fois b_{v} \fois d_{le} \fois f_{CV} \fois A_{st}^{\frac{2}{3}} \flèche droite \) Équation 2 (AS3600 Éq. 8.2.7.1)

ϕ = facteur de calcul de cisaillement
b₁= 1.1(1.6 – d_le/1000) ≥ 1.1 ou 1.1(1.6(1-d_le/1000) ≥ 0.8
b₂ = 1, pour les membres soumis à une flexion pure; ou
=1-(N^*/3.5A_g) ≥ 0 pour élément soumis à une traction axiale; ou
=1-(N^*/14A_g) pour éléments soumis à une compression axiale
b₃ = 1, ou peut être considéré comme –
2d_le/a_v mais pas supérieur à 2
a_v = distance pour la section à laquelle le cisaillement est considéré à la face de l'appui le plus proche
F_CV = f'c^1/3 ≤ 4 MPa
A_st = section transversale de l'armature longitudinale

La demande de cisaillement et la capacité de cisaillement doivent répondre à l'équation suivante pour répondre aux exigences de conception de l'AS 3600-09:

\(\texte{V}_{\texte{u}} \leq phi text{V}_{\texte{uc}} \flèche droite \) Équation 3 (par AS3600 Cl. 8.2.5)

Fondation SkyCiv, conformément à l'équation 3, calcule le rapport d'utilité de cisaillement unidirectionnel (Équation 4) en prenant la demande de cisaillement sur la capacité de cisaillement.

\( \texte{Rapport d'utilité} = frac{\texte{Demande de cisaillement}}{\texte{Capacité de cisaillement}} \flèche droite \) Équation 4

Cisaillement bidirectionnel

Le Cisaillement bidirectionnel état limite, aussi connu sous le nom poinçonnage, étend sa section critique à distance “j / 2” de la face de la colonne et autour du périmètre de la colonne (Figure 2) basé sur Clause AS3600 9.2.3(a).

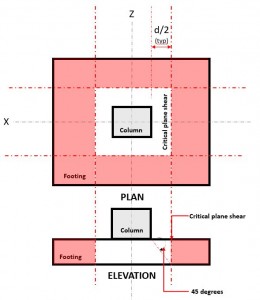
Figure 2. Plan de cisaillement critique du cisaillement bidirectionnel

Le Deux voiesentendre la demande ou V_u se produit au plan de cisaillement critique, situé à une distance de “j / 2” où le (rouge) zone hachurée, comme indiqué sur la figure 2.

Le bidirectionnel Capacité de cisaillement ou ϕV_euh est définie comme la résistance ultime au cisaillement et calculée à l'aide de l'équation 5 basé sur Clause AS3600 9.2.3

\( \phi V_{euh} = phi times u times f_{CV} \fois d rightarrow \) Équation 5 (AS3600 Cl. 9.2.3(a))

F_CV = 0.17(1 + 2/b_h) si’_c 0.34√f’_c
b_h = rapport de la longueur de la colonne sur l'axe Z sur l'axe X

d = distance entre la fibre de compression extrême et le centre de gravité de l'armature de tension longitudinale (mm)
u = longueur du périmètre de cisaillement critique (mm)

La demande de cisaillement et la capacité de cisaillement doivent répondre à l'équation suivante pour répondre aux exigences de conception de l'AS 3600:

\(\texte{V}_{\texte{u}} \leq phi text{V}_{\texte{euh}} \flèche droite \) Équation 6 (par AS3600 Cl. 8.2.5)

Fondation SkyCiv, conformément à l'équation 6, calcule le rapport d'utilité de cisaillement bidirectionnel (Équation 7) en prenant la demande de cisaillement sur la capacité de cisaillement.

\( \texte{Rapport d'utilité} = frac{\texte{Demande de cisaillement}}{\texte{Capacité de cisaillement}} \flèche droite \) Équation 7

Flexion

Dans un endroit isolé, la pression ascendante du sol provoque une flexion dans les deux sens avec des contraintes de traction à la surface inférieure. Les moments de flexion sont calculés dans chaque direction à la section 0.7a_souper distance du centre de la colonne, où a_souper est la moitié de la largeur de la colonne.

 

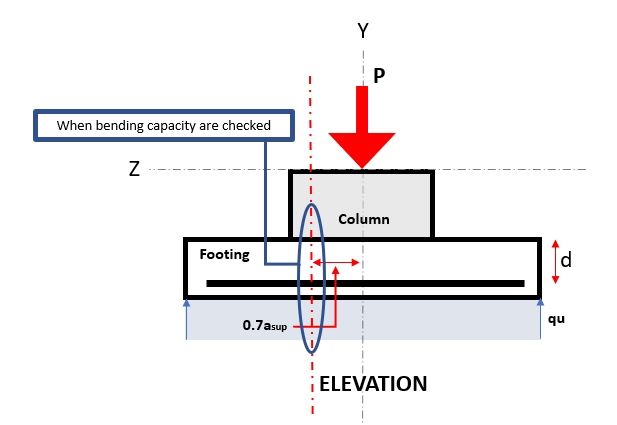
Figure 3. Section de flexion critique

Le Flexural l'état limite se produit à la section de flexion critique, situé 0.7a_souper du centre du pied (Reportez-vous à la figure 3).

Le Demande de flexion ou M_u est situé à la section de flexion critique indiquée sur la figure 3, et est calculé à l'aide de l'équation 8.

\( \texte{M}^{*}= q_{u} \fois D_{F} \fois gauche( \frac{ \frac{b_{F} – b_{c}}{2} }{2} \droite)^{2} \flèche droite \) Équation 8

Vérifications supplémentaires

Autres vérifications non mentionnées par le code, y compris les contrôles de pression du sol, soulèvement, et d'autres contrôles de stabilité sont également vérifiés.

Pression du sol

La détermination de la pression de base ou de l'interaction entre le sol et la semelle repose principalement sur les dimensions de la semelle et l'excentricité des charges appliquées qui en résulte.. En fonction du positionnement de cette excentricité résultante, la pression de base peut induire une compression totale ou partielle de la semelle. Cette évaluation nous permet de confirmer si le sol sous-jacent peut supporter l'intégralité des charges transmises depuis la semelle..

Pour un guide détaillé pour calculer manuellement la pression du sol, veuillez vous référer à ce lien: Répartition de la pression sous une semelle rectangulaire en béton

Le rapport d'utilité est évalué en comparant la pression maximale du sol (état de fonctionnement) avec la capacité portante brute admissible du sol:

 

\( \texte{Rapport d'utilité} = frac{\texte{Max. Pression du sol}}{\texte{Capacité portante brute admissible du sol}} \flèche droite \) Équation 14

Soulèvement

Vérifie la charge axiale déterminante agissant sur la semelle. Additionne toutes les charges verticales, y compris la charge utilisateur et le poids propre de la colonne., dalle de fondation, soil, et force de poussée. Si la colonne subit une force ascendante, les poids propres spécifiés doivent contrebalancer la force ascendante; autrement, la conception risque d'échouer en raison de l'instabilité.

Renversement

Le renversement de la semelle est vérifié en additionnant tous les instants autour d'un point de la semelle, y compris toutes les forces agissant sur celle-ci.. Toutes les combinaisons de charges de service doivent être prises en compte pour vérifier le moment de renversement déterminant.. Habituellement, un facteur de sécurité de 1.5-2 est utilisé pour évaluer si la semelle réussit le contrôle de renversement.

Glissement

Pour vérifier le glissement, la somme des charges résistantes horizontales dirigées vers la droite est divisée par la somme des charges dirigées vers la gauche.

• Charges stabilisantes:
  • Force horizontale due au frottement entre la base de la semelle et le sol de la sous-structure
  • Pression passive du sol (si inclus)
• Charges coulissantes:
  • La composante horizontale de la pression active du sol
  • La composante horizontale de la pression résultante de surcharge

En général, un facteur de sécurité minimum de 1.5 est utilisé. Si aucune force horizontale n’agit sur la semelle, la vérification du glissement n'est pas nécessaire.

Module de conception de la Fondation SkyCiv

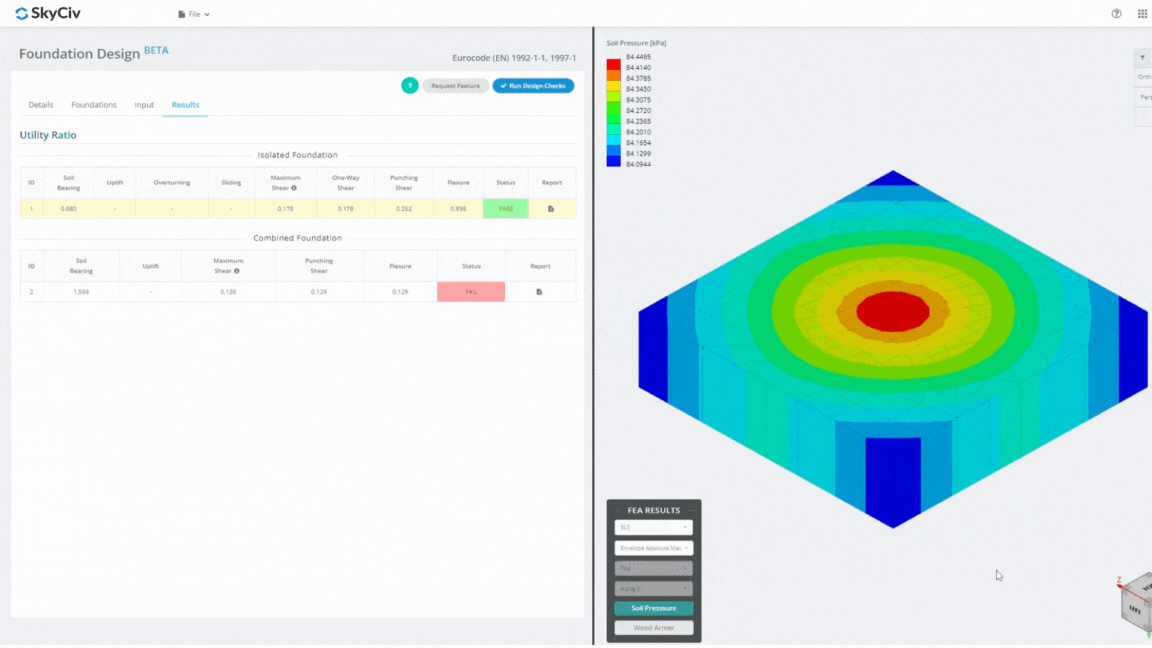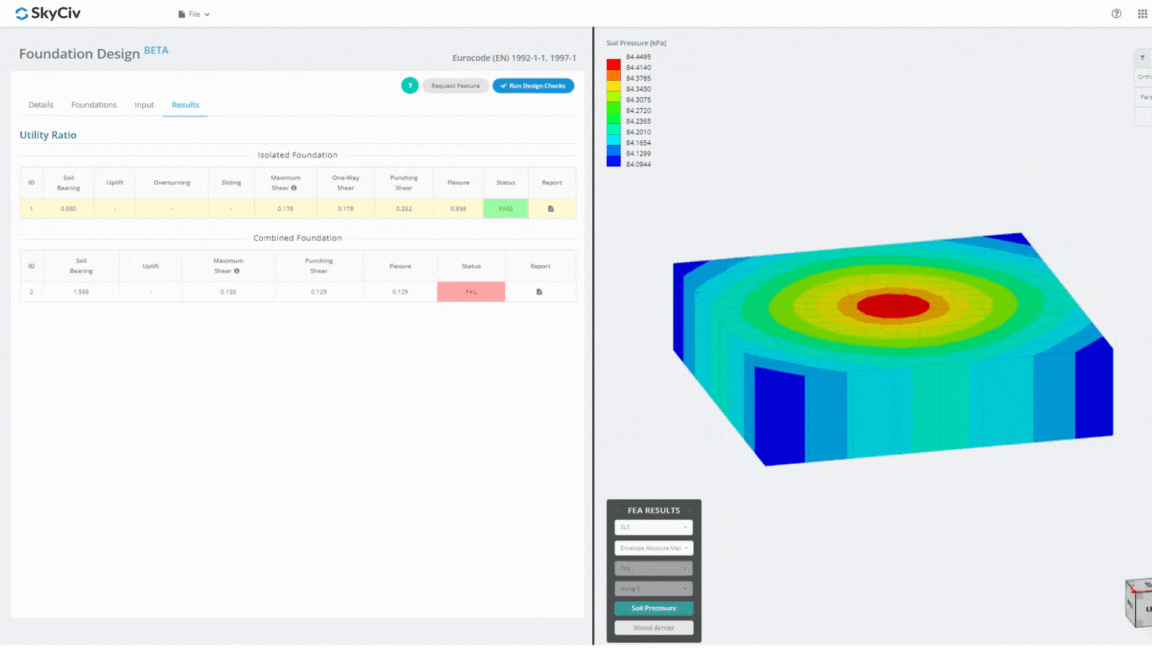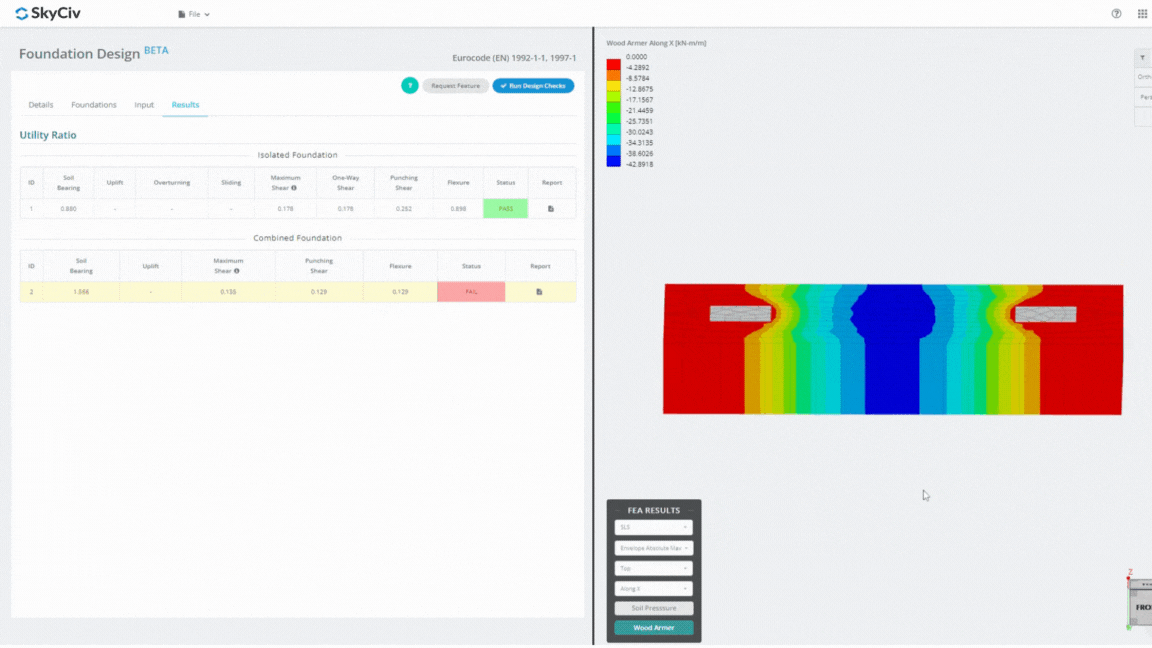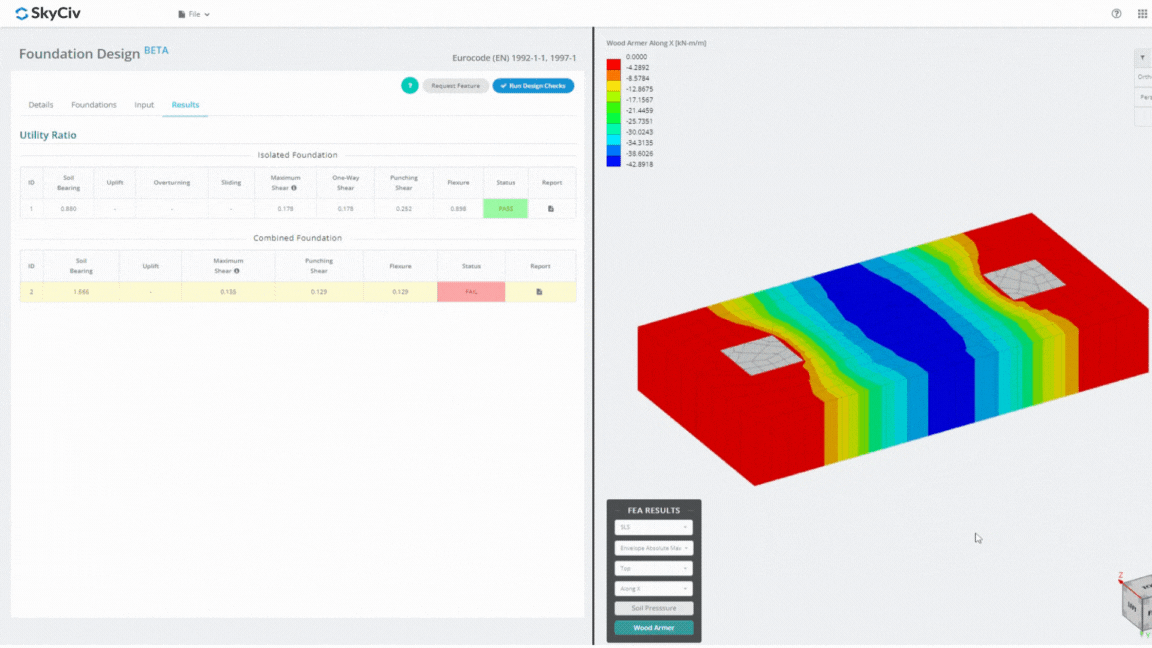
Le module de conception de fondation est un outil puissant intégré à l'analyse par éléments finis. (LAID), capable d'effectuer des analyses approfondies de la pression du sol et de l'armement du bois pour des contrôles de flexion détaillés. Il effectue tous les contrôles structurels spécifiés par l'ACI 318 et autres vérifications mentionnées ci-dessus et les présente dans un rapport complet.

Commencez avec la Fondation SkyCiv aujourd'hui!

Lancez le Conception de la fondation et essayez-le aujourd'hui! Il est facile de commencer, mais si vous avez besoin de plus d'aide, alors assurez-vous de visiter notre Documentation ou contactez-nous!

Pas un utilisateur de SkyCiv? Avec SkyCiv, vous pouvez même obtenir le poids de votre structure avant de la construire gratuits 14 Essai d'un jour pour commencer!

Références

1. Conseil australien des normes. (2009) Norme australienne AS3600-2009.
2. SJ Foster, AE Kilpatrick & Alerte RF. (2011) Notions de base sur le béton armé 2e édition.
3. Taylor, Andrew, et al. Le manuel de conception du béton armé: un compagnon de l'ACI-318-14. Institut américain du béton, 2015.
4. YC Loo & SH Chowdhury. (2013) Renforcé & Béton précontraint.