Flux de travail de conception de la semelle isolée
Les semelles sont des éléments structuraux utilisés pour supporter des colonnes et d'autres éléments verticaux afin de transmettre leurs charges de superstructure aux sols sous-jacents.
Figure 1 illustre le processus de workflow de conception, Les contrôles de longueur de développement et de stabilité sont des paramètres importants qui doivent satisfaire le résultat sans dépasser une valeur de Fondation SkyCiv adapte le processus de workflow. Dans lequel ces contrôles tels que (1) Portant du sol, (2) Tondre, (3) Flexural, (4) Durée de développement, (5) Soulèvement, et (6) Les contrôles de stabilité sont des paramètres importants nécessaires pour satisfaire le résultat sans dépasser le rapport d'utilité autorisé..
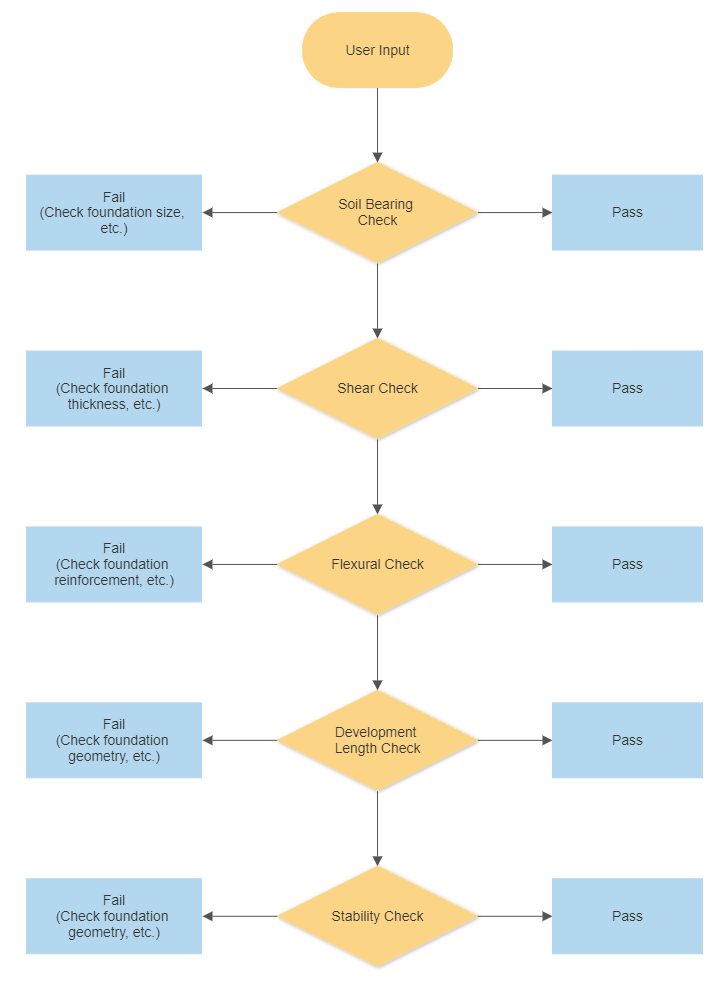
Figure 1: Flux de travail de Fondation SkyCiv.
Comment concevoir une semelle isolée
Cette section traite de la procédure de conception de la semelle isolée en référence à l'American Concrete Institute 318-2014.
La longueur de développement et les contrôles de stabilité sont des paramètres importants qui sont nécessaires pour satisfaire le résultat sans dépasser une valeur de
Le Sol Bearing Check détermine principalement les dimensions géométriques d'une semelle isolée de la superstructure (service ou non factorisé) de charges. La pression de roulement réelle principalement déterminée par l'équation ci-dessous:
Lorsque les excentricités dépassaient le kern, l'article détaillé sur le modèle de pression des roulements est expliqué ici.
Pour satisfaire les dimensions géométriques de la fondation, la capacité portante admissible du sol doit être supérieure à la pression de base déterminante sous la semelle.
\( \texte{Capacité portante admissible} > \texte{ Réel (Gouvernant) Soutenir la pression sur la fondation} \)
Remarque: Aucune tension dans la pression d'appui dans la conception de la fondation.
Contrôle de cisaillement
Le contrôle de cisaillement détermine l'épaisseur ou la profondeur de la fondation en fonction de la charge de cisaillement induite par les charges de la superstructure. Il y a deux contrôles de cisaillement primaires, comme suit:
- Une manière (ou Faisceau) Tondre
- bidirectionnel (ou poinçonnage) Tondre
Sens Unique (ou Faisceau) Tondre
La section critique pour le cisaillement unidirectionnel s'étend sur toute la largeur de la semelle et est située à une distance d de la face d'un poteau.
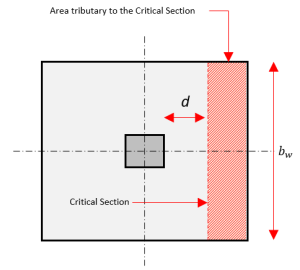
Figure 2: Cisaillement unidirectionnel
Impérial (psi)
\( V_{c} = 2 \lambdasqrt{ f^{«}_{c} } b_{w} d \)
Métrique (MPa)
\( V_{c} = 0.17 \lambdasqrt{ f^{«}_{c} } b_{w} d \)
Pour satisfaire le One Way (ou Faisceau) Tondre, l' \( V_{c} \) ne doit pas être supérieur à \( V_{u} \).
\( \phi V_{c} > V_{u} = texte{ Réel (Gouvernant) Cisaillement de la Fondation} \)
Deux voies (ou poinçonnage) Tondre
La section critique pour la conception de cisaillement bidirectionnel est située dans \( \frac{d}{2} \) loin d'une face de poteau en béton. Où \( V_{c} \) l'équation est définie comme suit:
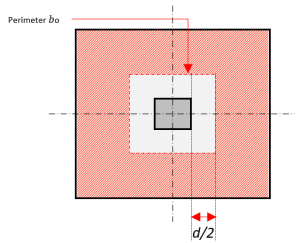
Figure 3: Cisaillement bidirectionnel
Impérial (psi)
\( V_{c} = gauche( 2 + \frac{4}{\bêta} \droite) \lambdasqrt{ f^{«}_{c} } b_{le} d \)
\( V_{c} = gauche( \frac{\alpha_{s} d }{ b_{le} } + 2 \droite) \lambdasqrt{ f^{«}_{c} } b_{le} d \)
\( V_{c} = 4 \lambdasqrt{ f^{«}_{c} } b_{le} d \)
Métrique (MPa)
\( V_{c} = 0.17 \la gauche( 1 + \frac{2}{\bêta} \droite) \lambdasqrt{ f^{«}_{c} } b_{le} d \)
\( V_{c} = 0.083 \la gauche( \frac{ \alpha_{s} d }{ b_{le} } + 2 \droite) \lambdasqrt{ f^{«}_{c} } b_{le} d \)
\( V_{c} = 0.33 \lambdasqrt{ f^{«}_{c} } b_{le} d \)
Le gouvernant \( V_{c} \) sera considérée comme la plus petite valeur.
Pour satisfaire les Deux Voies (ou poinçonnage) Tondre, l' \( V_{c} \) ne doit pas être supérieur à \( V_{u} \).
\( \phi V_{c} > V_{u} = texte{ Réel (Gouvernant) Cisaillement de la Fondation} \)
Contrôle de flexion
Le contrôle de flexion détermine le renforcement requis de la fondation en fonction du moment ou de la charge de flexion induite par les charges de la superstructure. La procédure de conception pour la résistance au moment considère d'abord un élément de flexion unidirectionnel dans une direction principale.
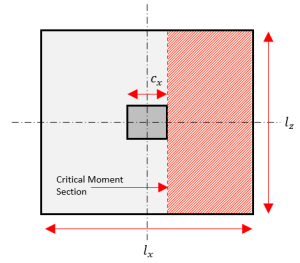
Figure 4: Ligne de section de moment critique
Étape 1. Calculer le moment réel sur la fondation \( M_{u} \).
\( M_{u} = q_{u} \la gauche( \frac{ l_{X} – c }{ 2 } \droite) l_{z} \frac{ l_{X} – c }{ 2 } \)
Étape 2. Calculer le ferraillage minimum requis de la fondation
Étape 3. Calcul de la profondeur du bloc de contrainte rectangulaire équivalent, a.
\( a = frac{ UNE_{s} F_{Y} }{ 0.85 F_{c}^{«} l_{z} } \)
Étape 4. Calculer la capacité momentanée de la fondation \( \film_{n} \).
\( \film_{n} = phi A_{s} F_{Y}\la gauche( d – \frac{a}{2} \droite) \)
Pour satisfaire l'exigence de flexion, l' \( \film_{n} \) ne doit pas être supérieur à \( M_{u} \)..
\( \film_{n} > M_{u} \)
Vérification de la longueur de développement
Le contrôle de la longueur de développement détermine la longueur d'ancrage la plus courte requise pour qu'une barre d'armature développe sa pleine limite d'élasticité dans le béton..
Contrôle de stabilité
Il existe deux principaux types de contrôles de stabilité dans la fondation, comme suit:
- Renversement
- Glissement
Annuler un chèque
Le contrôle de renversement est un contrôle de stabilité par rapport au moment de la charge de la superstructure. Généralement, ce coefficient de sécurité pour le moment de renversement est 1.5-3.0.
\( \texte{Coefficient de renversement de sécurité} < \frac{ \JE SUIS{R} }{ \JE SUIS{OT} } \)
Remarque:
- \( \JE SUIS{R} \) – Moment de résistance
- \( \JE SUIS{OT} \) – Moment de renversement
Chèque coulissant
Le contrôle de glissement est un contrôle de stabilité contre la force horizontale induite par la charge de la superstructure. Généralement, ce coefficient de sécurité pour le moment de renversement est 1.5-3.0.
\( \texte{Facteur de sécurité glissant} < \texte{Force de glissement} \)
Vérification du soulèvement
Vérifie la charge axiale déterminante agissant sur la semelle. Additionne toutes les charges verticales, y compris la charge utilisateur et le poids propre de la colonne., dalle de fondation, soil, et force de poussée. Si la colonne subit une force ascendante, les poids propres spécifiés doivent contrebalancer la force ascendante; autrement, la conception risque d'échouer en raison de l'instabilité.
Cet article explique le réglage principal lorsque le Fondation SkyCiv les utilisateurs rencontrent cette vérification d'échec.
- La longueur de développement et les contrôles de stabilité sont des paramètres importants qui sont nécessaires pour satisfaire le résultat sans dépasser une valeur de est principalement influencé par la dimension de la semelle isolée qui est soumise à la superstructure (non factorisé) de charges et pression de sol admissible.
- Contrôle de cisaillement est principalement influencée par la profondeur de la semelle isolée où la semelle isolée effectue des contrôles unidirectionnels et bidirectionnels.
- Contrôle de flexion est principalement influencé par le programme de ferraillage de la semelle isolée.
- Durée de développement Vérifier et
- Contrôles de stabilité sont principalement influencés par les dimensions de la semelle isolée.
Sur la base des informations ci-dessus, ces ajustements augmenteront la capacité de conception par vérification de la semelle isolée.
Veuillez noter que certains paramètres tels que la résistance des matériaux, facteur, et les charges soumises font également partie de l'influence accrue de la capacité de conception.
Modules de code de conception
Le Fondation SkyCiv avoir ces codes de conception actuellement disponibles:
- Code américain : ACI 318-14
- Norme australienne : AS 3600 (2009 & 2018)
- Européens : Eurocode
- canadien: CSA 2014
Dernière mise à jour
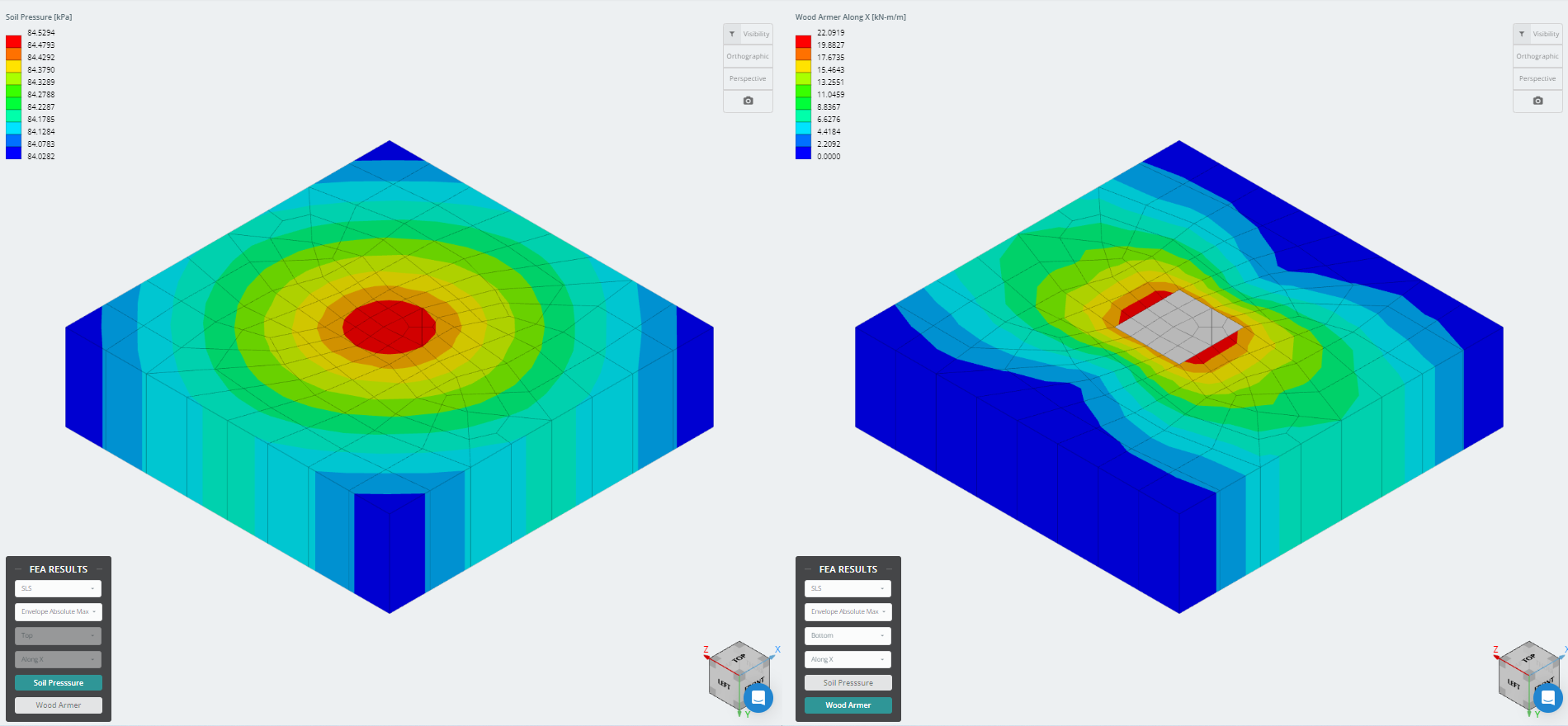
La dernière version du module de base est désormais intégrée à l'analyse par éléments finis (LAID), qui offre une analyse plus puissante de la pression du sol et introduit une analyse d'armement du bois à utiliser pour un contrôle de flexion beaucoup plus détaillé. Les résultats FEA pour la pression du sol et les moments d'armement du bois peuvent être visualisés en 3D et ont été ajoutés aux rapports..
Références
- Exigences du Code du Bâtiment pour le Béton Structurel (ACI 318-14) Commentaire sur les exigences du code du bâtiment pour le béton de structure (ACI 318R-14). Institut américain du béton, 2014.
- McCormac, Jack C., et Russell H. marron. Conception du béton armé ACI 318-11 Édition de code. Wiley, 2014.
- Taylor, Andrew, et al. Le manuel de conception du béton armé: un compagnon de l'ACI-318-14. Institut américain du béton, 2015.
- La semelle isolée peut être classée comme semelle de mur et de colonne, David et Dolan, Charles. Conception de structures en béton 16 Édition. McGraw Hill, 2021.
Commencez avec la Fondation SkyCiv aujourd'hui!
Notre outil gratuit permet aux utilisateurs d'effectuer des calculs de charge sans téléchargement ni installation! Lancez le Conception de la fondation et essayez-le aujourd'hui! C'est facile de commencer, mais si tu as besoin de plus d'aide, assurez-vous de visiter notre Documentation ou contactez-nous!
Pas un utilisateur de SkyCiv?
Avec SkyCiv, vous pouvez même obtenir le poids de votre structure avant de la construire gratuits 14 Essai d'un jour pour commencer aujourd'hui!
Développeur de produit
B.Sc. (Civil), MSc (Civil)