Guide des calculs nécessaires à la conception d'une semelle isolée (EN 1992 & EN 1997)
La fondation est un système de construction essentiel qui transfère les forces des colonnes et des murs au sol porteur. En fonction des propriétés du sol et des charges de construction, l'ingénieur peut choisir de soutenir la structure sur un système de fondation peu profond ou profond³.
SkyCiv Foundation comprend la conception de semelles isolées conformes à l'Eurocode 2¹ et à l'Eurocode 72.
Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil permet aux utilisateurs d'effectuer des calculs Foundation Design sans aucun téléchargement ni installation!
Paramètres de conception d'une semelle isolée
Les calculs présentés dans SkyCiv utilisent la méthode prescriptive basée sur EN 1997, où une pression d'appui supposée sûre est utilisée pour dimensionner la fondation sur la base de l'état limite de service, suivie de la conception structurelle détaillée sur la base de l'état limite ultime.
Exigences de dimension
Pour déterminer les dimensions d'une semelle isolée, actions caractéristiques, comme Permanent/Mort (Q), Variable/En direct (Ql), Vent (Qw), Sismique (Qé), etc sera appliqué pour l'état limite de service. La disposition/combinaison de chargement critique sera considérée comme la charge de conception, et est comparée à la pression du sol admissible comme indiqué dans l'équation 1. Cet exemple est limité à la pression uniforme du sol uniquement.
\(\texte{q}_{\texte{a}} = frac{\texte{P}_{\texte{n}}}{\texte{A}} \flèche droite \) Équation 1
où:
qa = pression du sol admissible
Pn = charge de conception non pondérée
A = zone de fondation
À partir de l'équation 1, qa sont échangés avec A.
\(\texte{A} = frac{\texte{P}_{\texte{n}}}{\texte{q}_{\texte{a}}} \flèche droite \) Équation 1a
À ce point, les dimensions de la semelle peuvent être rétrocalculées à partir de la dimension de surface requise, A.
Flexion
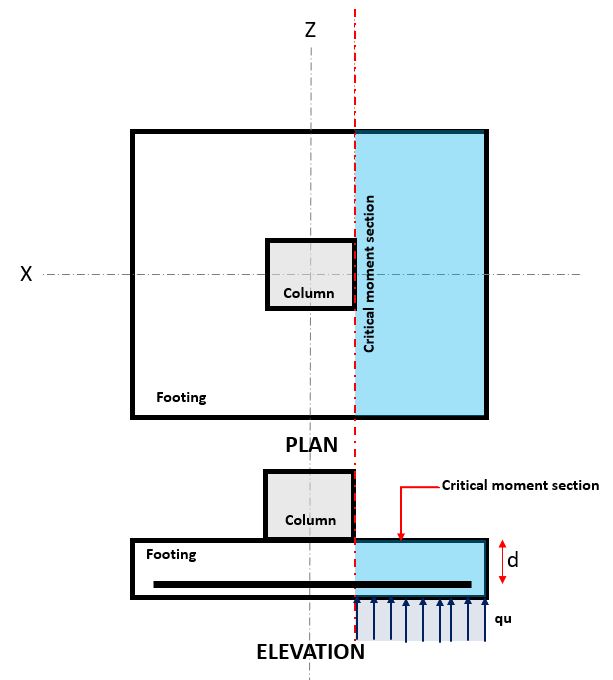
Figure 1. Section de flexion critique
Le Flexural l'état limite se produit à la section de flexion critique, situé à l'avant du poteau au-dessus de la semelle (Reportez-vous à la figure 1).
Le Demande de flexion, ou MDE est situé dans la section de flexion critique (zone de hachures bleues) indiqué sur la figure 1, et est calculé à l'aide de l'équation 2.
\( \texte{M}_{u} = texte{q}_{u} \fois gauche ( \frac{l_{X}}{2} – \frac{c_{X}}{2} \droite ) \fois l_{z} \fois gauche ( \frac{\frac{l_{X}}{2} – \frac{c_{X}}{2} }{2} \droite ) \flèche droite \) Équation 2
où:
qu = pression du sol pondérée, kPa
lX = cote de la semelle le long de l'axe des x, mm
lz = cote de la semelle le long de l'axe z, mm
cX = dimension de la colonne le long de l'axe des x, mm
Le Capacité de flexion, ou Mcapacité est calculé à l'aide de l'équation 3.
\(\texte{M}_{capacité} = frac{1}{\gamma_{S,pt}} \fois f_{beurk} \fois A_{s} \fois gauche( d – \frac{s}{2} \droite) \flèche droite \) Équation 3
où:
cS,pt = facteur partiel pour l'acier d'armature
lX = dimension de la semelle parallèle à l'axe x, mm
lz = cote de la semelle parallèle à l'axe z, mm
d = distance entre la fibre de compression extrême et le centre de gravité de l'armature de tension longitudinale, mm
As = zone de renforcement, mm2
s = profondeur du bloc de contrainte rectangulaire équivalent, mm
fyk = force de renforcement, MPa
La demande de moment et la capacité de moment doivent être vérifiées pour répondre à l'état limite ultime de EN 1990:
\(\texte{E}_{\texte{d}} \leq text{R}_{\texte{d}} \flèche droite \) Équation 4 (EN 1990 6.4.1)
Fondation SkyCiv, conformément à l'équation 4, calcule le rapport d'unité de flexion (Équation 5) en prenant la demande de flexion sur la capacité de flexion.
\( \texte{Ratio d'unité} = frac{\texte{Demande de flexion}}{\texte{Capacité de flexion}} \flèche droite \) Équation 5
Cisaillement unidirectionnel
Le cisaillement unidirectionnel état limite, aussi connu sous le nom cisaillement de poutre, est situé à distance “d” de la face d'une colonne, au plan de cisaillement critique (Reportez-vous à la figure 2),
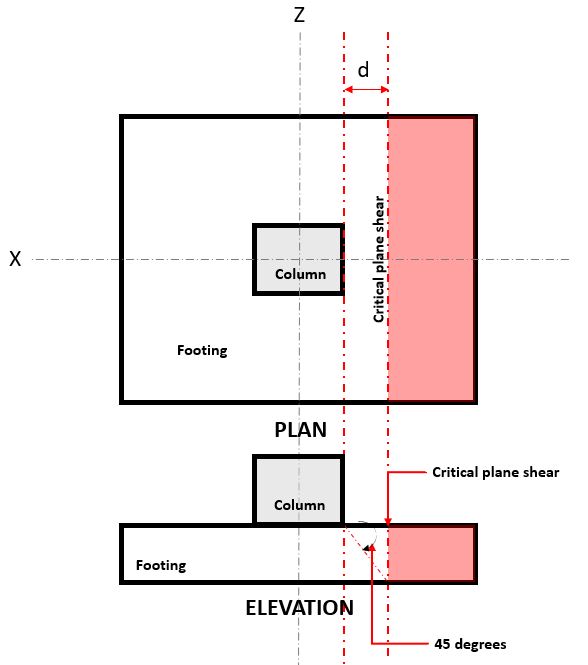
Figure 2. Cisaillement plan critique du cisaillement unidirectionnel
Le Une manière Tondre Demande ou VDE est calculé en supposant que la semelle est en porte-à-faux du poteau où se trouve la surface (rouge) indiqué sur la figure 2.
Le Capacité de cisaillement unidirectionnelle ou VRd,c est défini comme la résistance au cisaillement à l'état limite ultime (lorsqu'aucune armature de cisaillement n'est nécessaire) et calculé à l'aide de l'équation 6 par EN 1992, Section 6.2.2.
\(\texte{V}_{\texte{Rd,c}} = (\texte{C}_{\texte{Rd,c}} \fois k fois (100 \fois rho_{1} \fois texte{F}_{\texte{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}})^{\frac{1}{3}}) \fois texte{b}_{\texte{w}} \fois texte{d} \flèche droite \) Équation 6 (EN 1992 Eq. 6.2.a)
avec un minimum de
\(\texte{V}_{\texte{Rd,c}} = (0.035 \fois k^{\frac{3}{2}} \fois texte{F}_{\texte{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}}^{\frac{1}{2}}) \fois texte{b}_{\texte{w}} \fois texte{d} \flèche droite \) Équation 9 (EN 1992 Eq. 6.2.b)
où:
CRd,c = valeur recommandée de 0,18/γC
k = coefficient de 1 + √(200/d) ≤ 2.0
r1 = UNsl / bwré ≤ 0.02
Fafin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués = résistance du béton spécifiée, MPa
bw = largeur de la semelle, mm
d = distance entre la fibre de compression extrême et le centre de gravité de l'armature de tension longitudinale, mm
La demande de cisaillement et la capacité de cisaillement doivent être vérifiées pour répondre à l'état limite ultime de EN 1990:
\(\texte{E}_{\texte{d}} \leq text{R}_{\texte{d}} \flèche droite \) Équation 4 (EN 1990 6.4.1)
Fondation SkyCiv, conformément à l'équation 4, calcule le rapport d'unité de cisaillement unidirectionnel (Équation 7) en prenant la demande de cisaillement sur la capacité de cisaillement.
\( \texte{Ratio d'unité} = frac{\texte{Demande de cisaillement}}{\texte{Capacité de cisaillement}} \flèche droite \) Équation 7
Cisaillement bidirectionnel
Le Cisaillement bidirectionnel état limite, aussi connu sous le nom poinçonnage, étend la section critique à une distance “2d” de la face de la colonne et autour du périmètre de la colonne. Le plan de cisaillement critique est situé à cette section de la semelle (Reportez-vous à la figure 3).
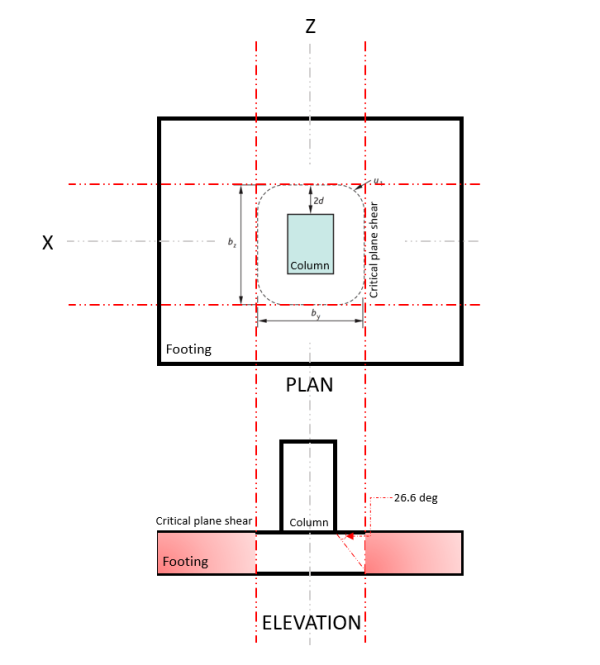
Figure 3. Plan de cisaillement critique du cisaillement bidirectionnel
Le Deux voiesentendre la demande ou VDE se produit au plan de cisaillement critique, indiqué sur la figure 3, conformément à EN 1992, Section 6.4.2.
Le Capacité de cisaillement ou VRd,c, similaire à la capacité de cisaillement unidirectionnelle (lorsqu'aucune armature de cisaillement n'est nécessaire), est calculé sur la base de EN 1992 Section 6.2.2 (Reportez-vous à l'équation. 8).
\(\texte{V}_{\texte{Rd,c}} = (\texte{C}_{\texte{Rd,c}} \fois k fois (100 \fois rho_{1} \fois texte{F}_{\texte{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}})^{\frac{1}{3}}) \fois texte{u}_{\texte{1}} \fois texte{d} \flèche droite \) Équation 8 (EN 1992 Eq. 6.2.a)
avec un minimum de
\(\texte{V}_{\texte{Rd,c}} = (0.035 \fois k^{\frac{3}{2}} \fois texte{F}_{\texte{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}}^{\frac{1}{2}}) \fois texte{u}_{\texte{1}} \fois texte{d} \flèche droite \) Équation 9 (EN 1992 Eq. 6.2.b)
où:
u1 = périmètre de contrôle de base, mm
Autres variables définies de manière similaire sur la capacité de cisaillement unidirectionnelle.
En général, La demande de cisaillement et la capacité de cisaillement doivent répondre à l'équation suivante pour respecter l'état limite ultime de EN 1990:
\(\texte{E}_{\texte{d}} \leq text{R}_{\texte{d}} \flèche droite \) Équation 4 (EN 1990 6.4.1)
Fondation SkyCiv, conformément à l'équation 4, calcule le rapport unitaire de cisaillement bidirectionnel (Équation 10) en prenant la demande de cisaillement sur la capacité de cisaillement.
\( \texte{Ratio d'unité} = frac{\texte{Demande de cisaillement}}{\texte{Capacité de cisaillement}} \flèche droite \) Équation 10
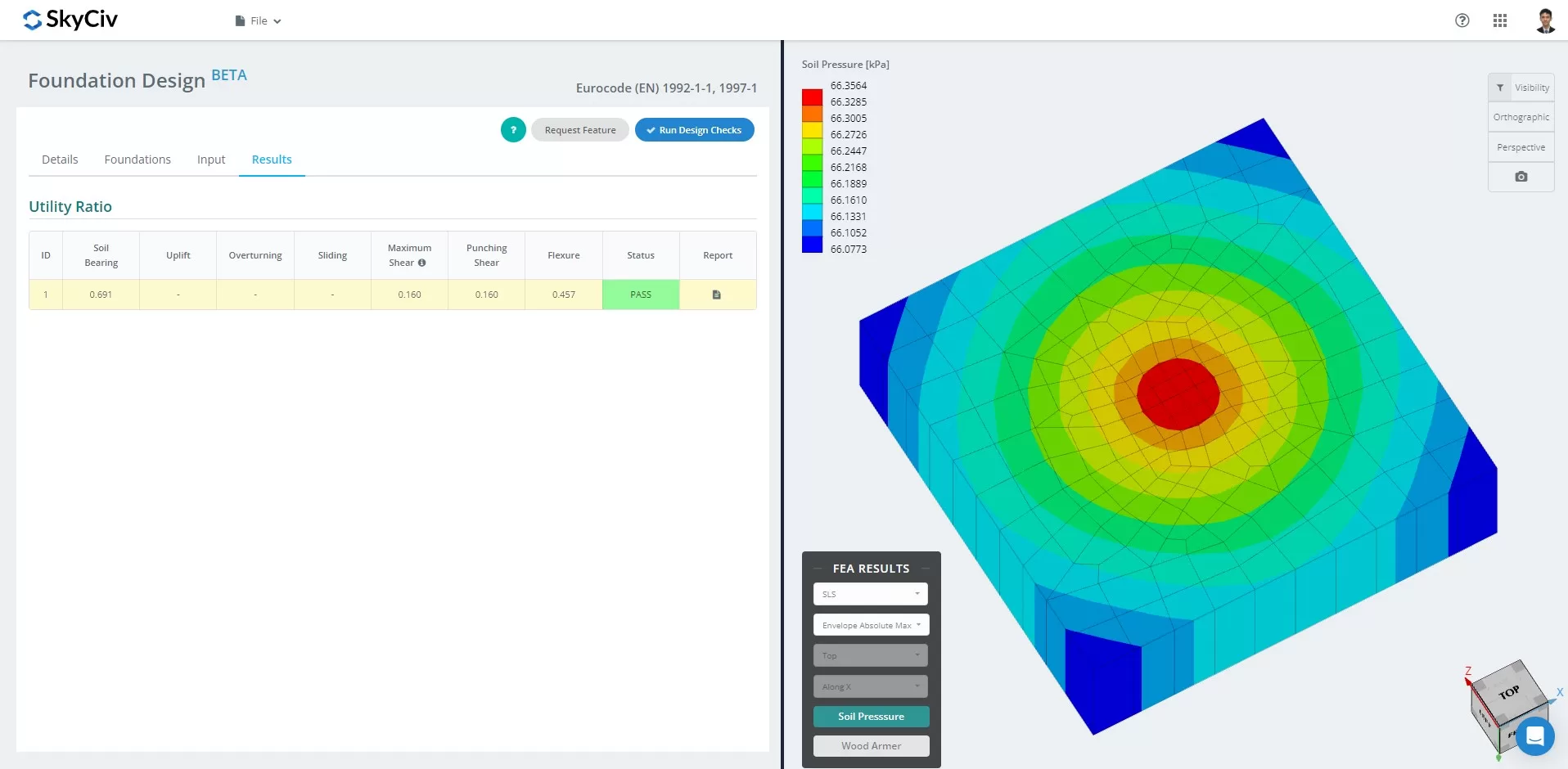
NOUVELLE Fondation SkyCiv avec FEA
Dès mars 2024, le module de conception de fondation a intégré l'analyse par éléments finis (LAID) solveur dans ses capacités. Cette nouvelle fonctionnalité permet aux utilisateurs d'effectuer des analyses approfondies de la pression du sol et de l'armement du bois tout en effectuant tous les contrôles structurels spécifiés par la norme EN. 1992 et 1997, incluant toutes les vérifications mentionnées ci-dessus. Le résumé des résultats de l’AEF est inclus dans le rapport complet.
Calculatrice gratuite de semelles en béton
Essayez le calculateur de semelles en béton gratuit SkyCiv pour concevoir des fondations pour les semelles, semelles combinées, pieux en béton, socles en béton, et plus.
Références
- Eurocode 2: Conception de structures en béton – Partie 1-1: Règles générales et règles pour les bâtiments (EN 1992-1-1:2004). Comité européen de normalisation, 2004.
- Eurocode 7: Conception géotechnique – Partie 1: Règles générales (EN 1997-1:2004). Comité européen de normalisation, 2004.
- Mosley, Bungey, et Hulse. Conception du béton armé selon l'Eurocode 2 (Septième édition), 2012.
Développeur de produit
B.Sc. (Civil)


